Detect Cycle in an Undirected Graph using DFS (with code)

Learning to solve competitive questions is the first step to preparing for any technical interview. In this article, we will learn how to check if an undirected graph contains a cycle or not. It is most likely to be asked during the technical discussions of product-based companies to test your basic knowledge and understanding of a graph. 

Detect Cycle in Undirected Graph Problem

First of all, we need to revise what a graph is. It is a data structure that comprises a restricted set of vertices (or nodes) and edges that connect these vertices. A graph G is an ordered pair G = (V, E), where V is the set of vertices (also called nodes or points) and E is the set of edges in G. In this case, we say that G consists of a set V of vertices and E ⊆ V × V.

Graphs are often used to model relationships between objects.  They can be directed or undirected. In an undirected graph, the edges are unordered pairs of vertices, whereas, in a directed graph, the edges have an order to them.

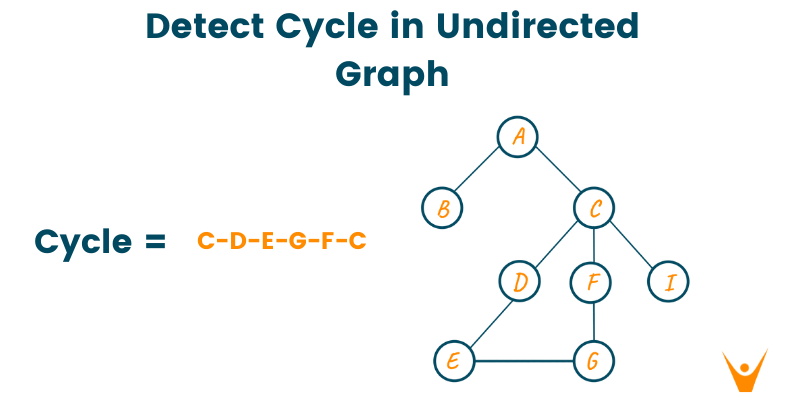
Now, what is a Cycle in a Graph? The path which starts from any given vertex and ends at the same vertex is called the cycle of the graph. The below image shows an example of graph data structure, and we can see that node A-B-D-C-A results in the cycle of the graph.

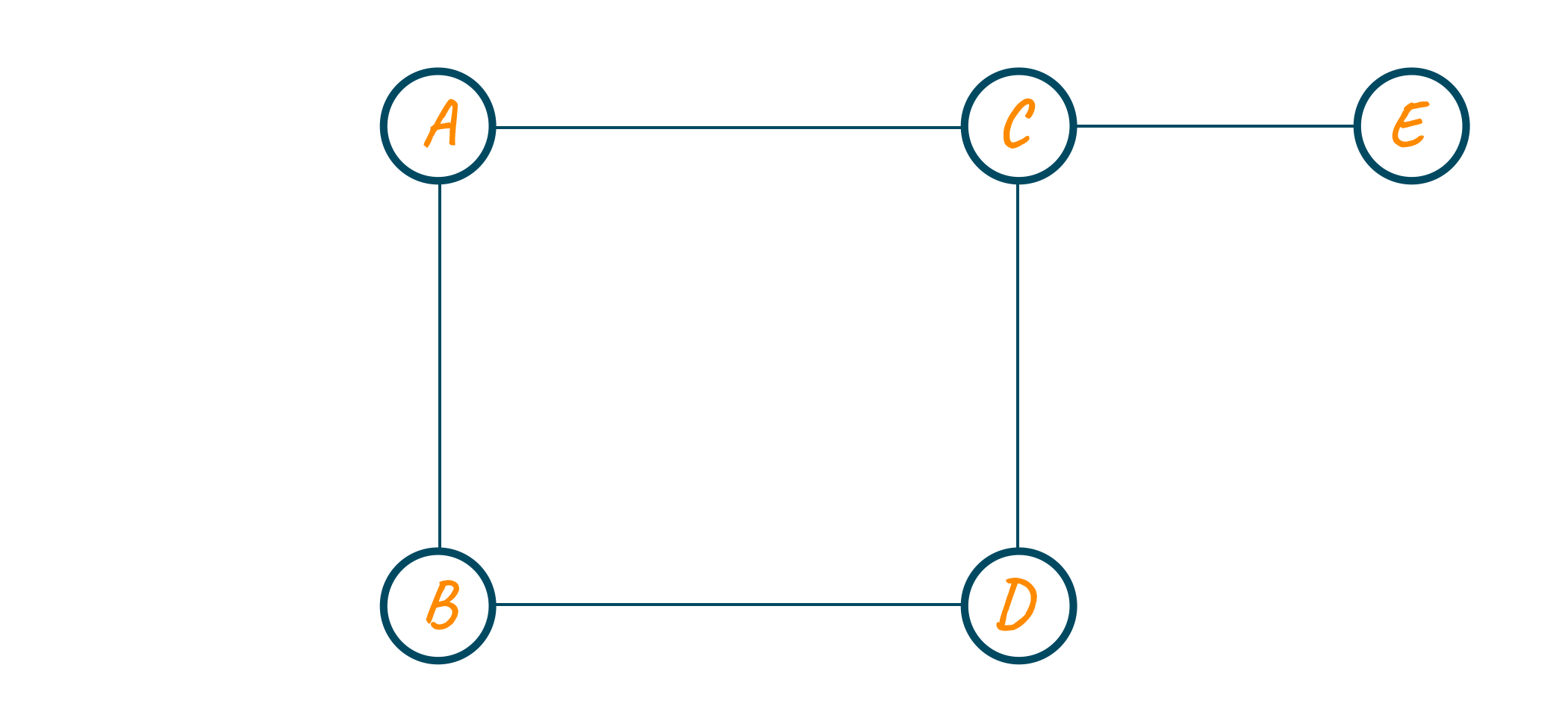
So, here is the problem statement we are going to solve: Given a connected undirected graph, check if it contains any cycle or not.

Can we detect a cycle in an undirected graph? Yes. If a graph doesn't include any cycles, it is deemed to be acyclic; if it does, it is considered to be cyclic. There is a cycle throughout the graph if we come across a visited vertex that has a parent that's not the present node.

How to Detect Cycle in an Undirect Graph?

Consider the below graph which contains cycle C-D-E-G-F-C

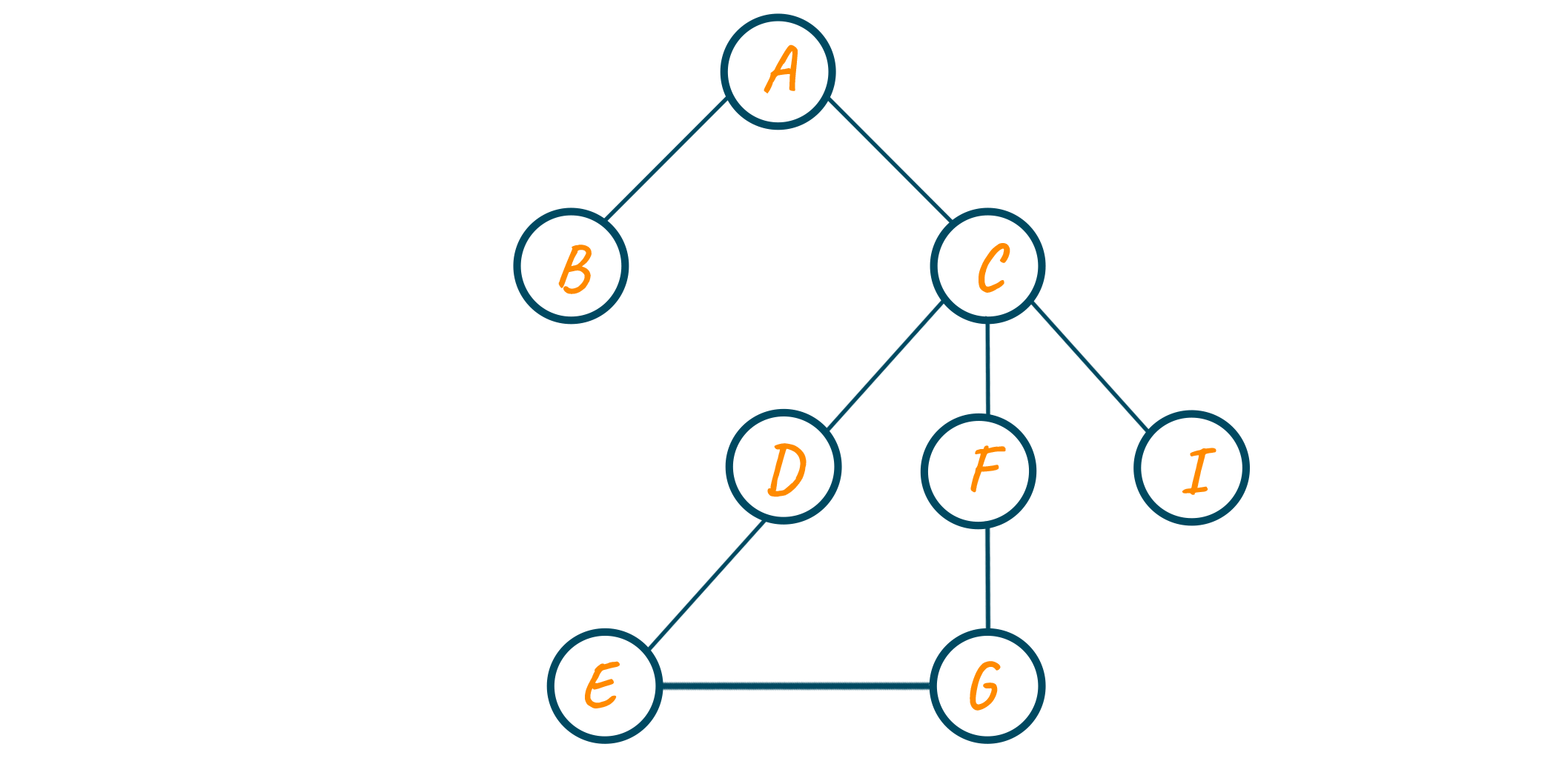
Given a graph and an unvisited node, run a Depth First Search traversal from the unvisited node to detect cycles in the graph. A DFS of a connected graph produces a tree. A graph has a cycle if and only if it contains a back edge. A back edge is an edge joining a node to itself or one of its ancestors in the depth-first search tree produced by the DFS algorithm.

To find the back edge of a node, keep track of nodes that have already been visited. If a back edge to any visited node is encountered, there is a loop and return true.

Sounds confusing?

Let us look at the example below for a better understanding:

Consider the below graph to detect cycles in the undirected graphs using the DFS approach. We will also require a parent variable to keep track of the node we are just coming from.

Initially, all the vertex are unvisited and since there is no parent of node A, we assign its parent equal to -1.

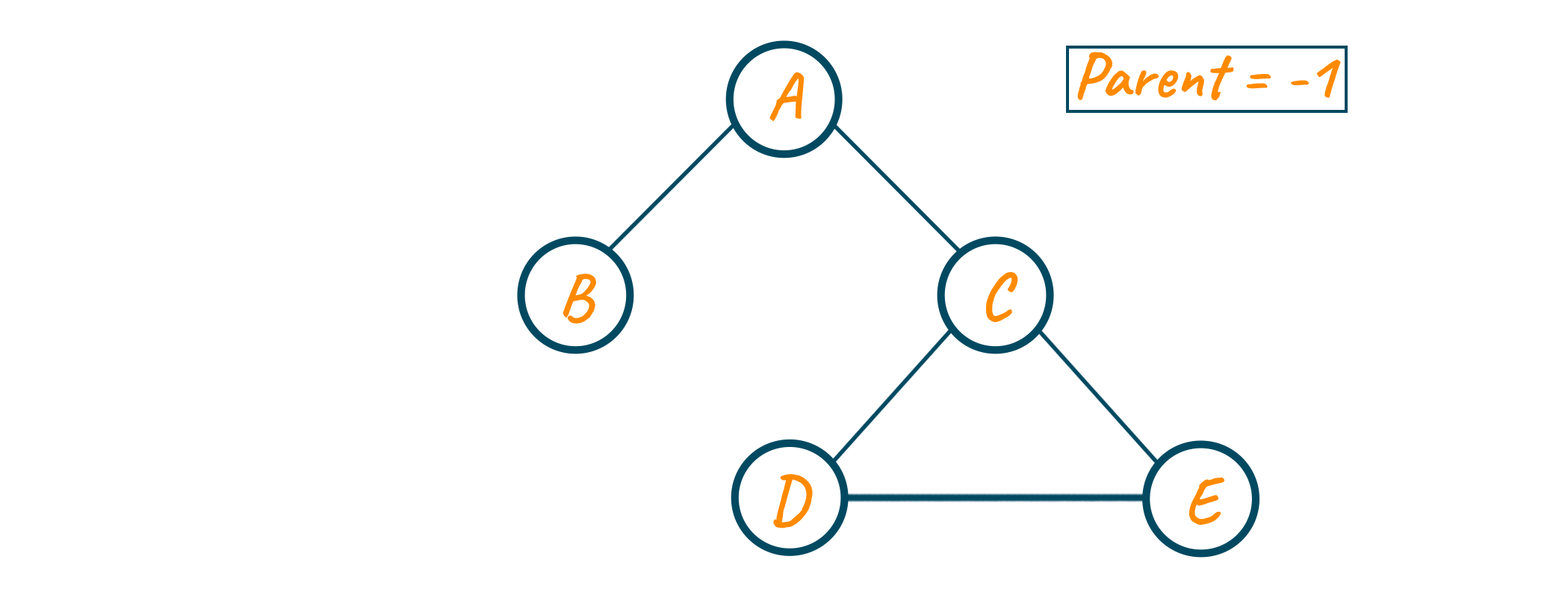
Now we start our DFS traversal. Since node A is unvisited, we visit it and its neighbor node are B and C. We go to node B first. Since it’s unvisited, we visit it and also note that the parent variable is now node A as we are coming from node A.

Now for node B, the only neighboring node is A which is visited and also the parent of node B, so we backtrack to node A.

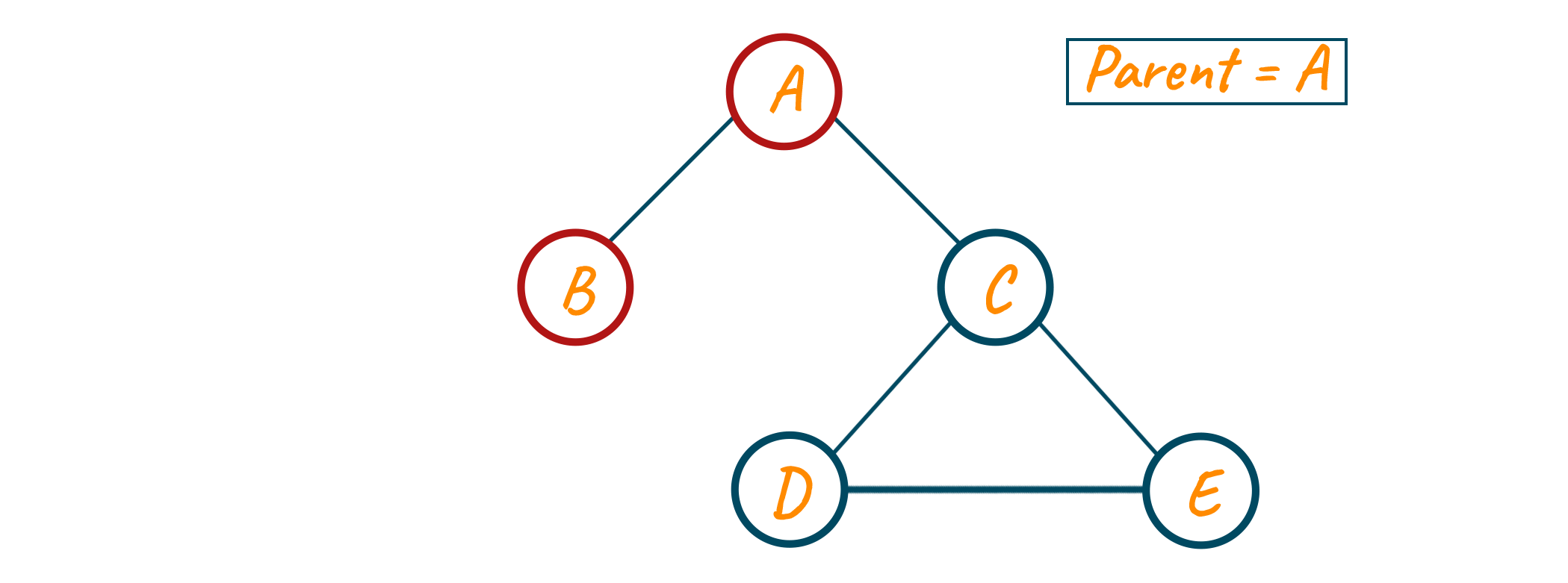
Now from node A, the unvisited neighbor is node C. We visit node C, since we are coming from node A, the parent remains equal to node A.

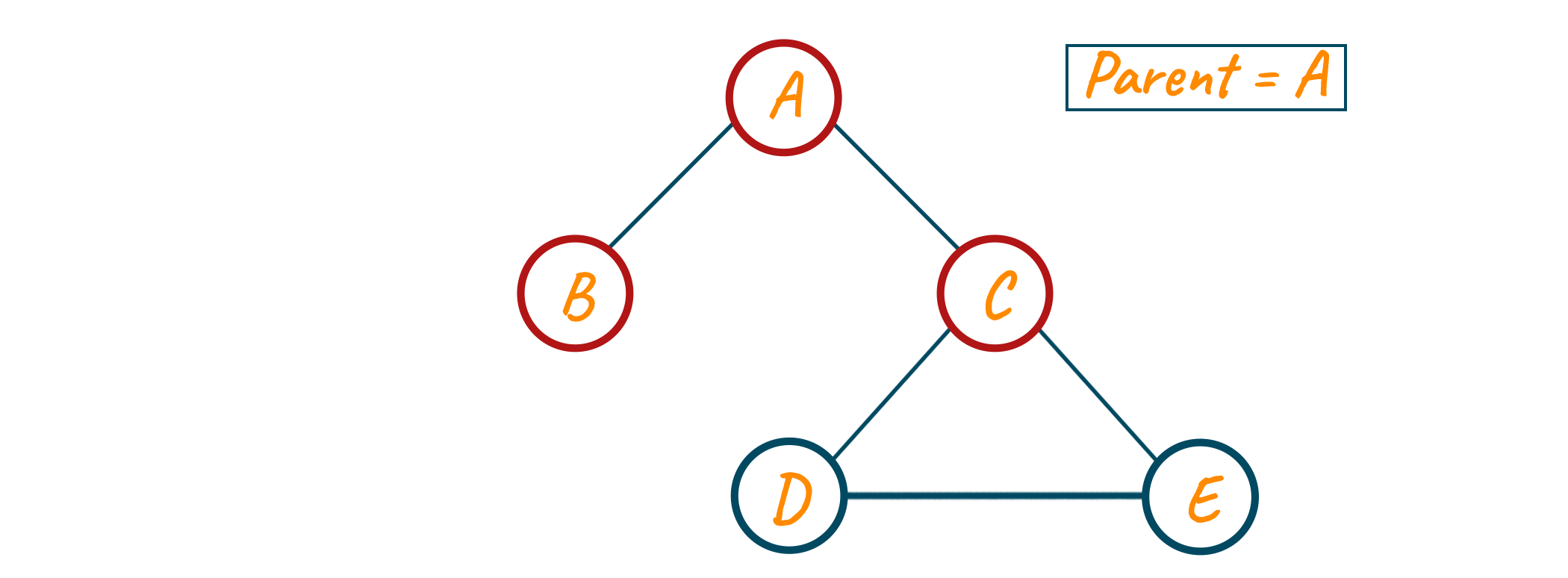
Now from node C, we have node 3 neighbors. First is node A which is visited but is the parent of node C, and the other is node D and node E which are unvisited. Therefore, we move to node D.

We visit node D and update our parent variable to node C as shown in the below image.

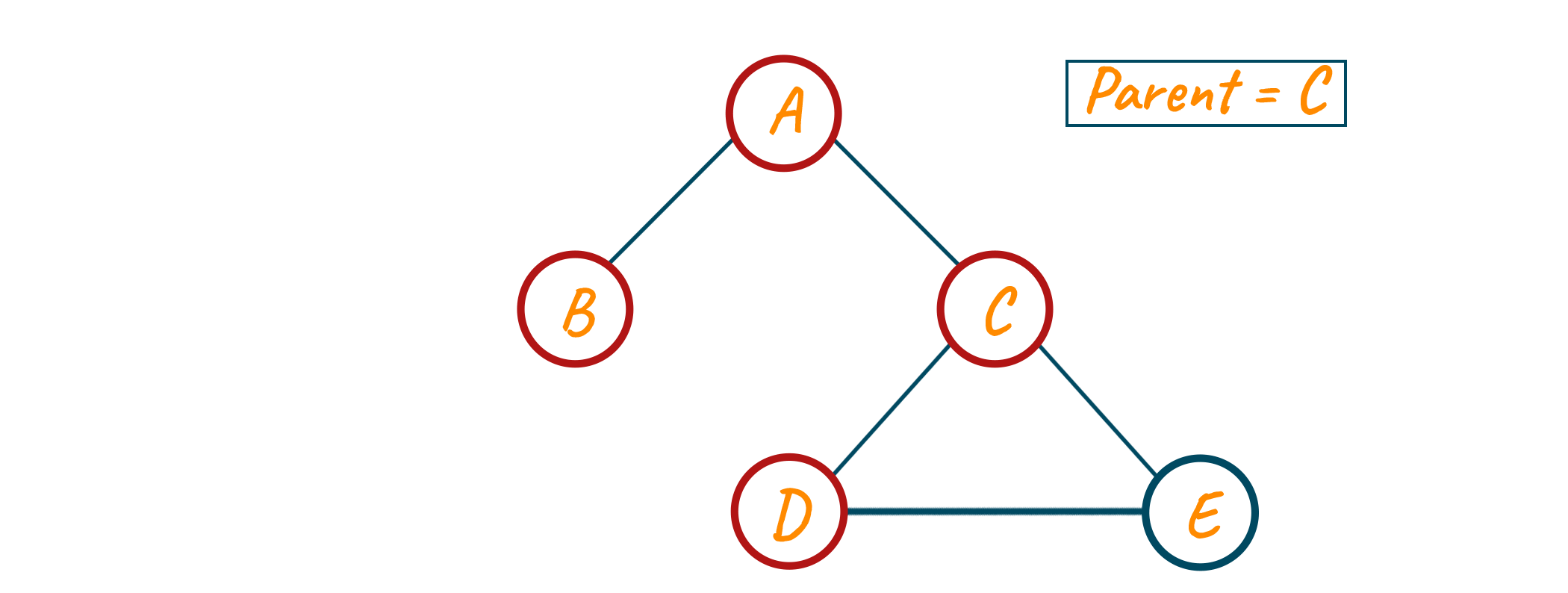
Now from node D, we have node C and node E as neighbors. Here, node C is visited but the parent of node D so we move to the unvisited neighbor of node E. At last, we mark node E as visited. And also note that since we are coming from node D, we update our parent variable to node D.

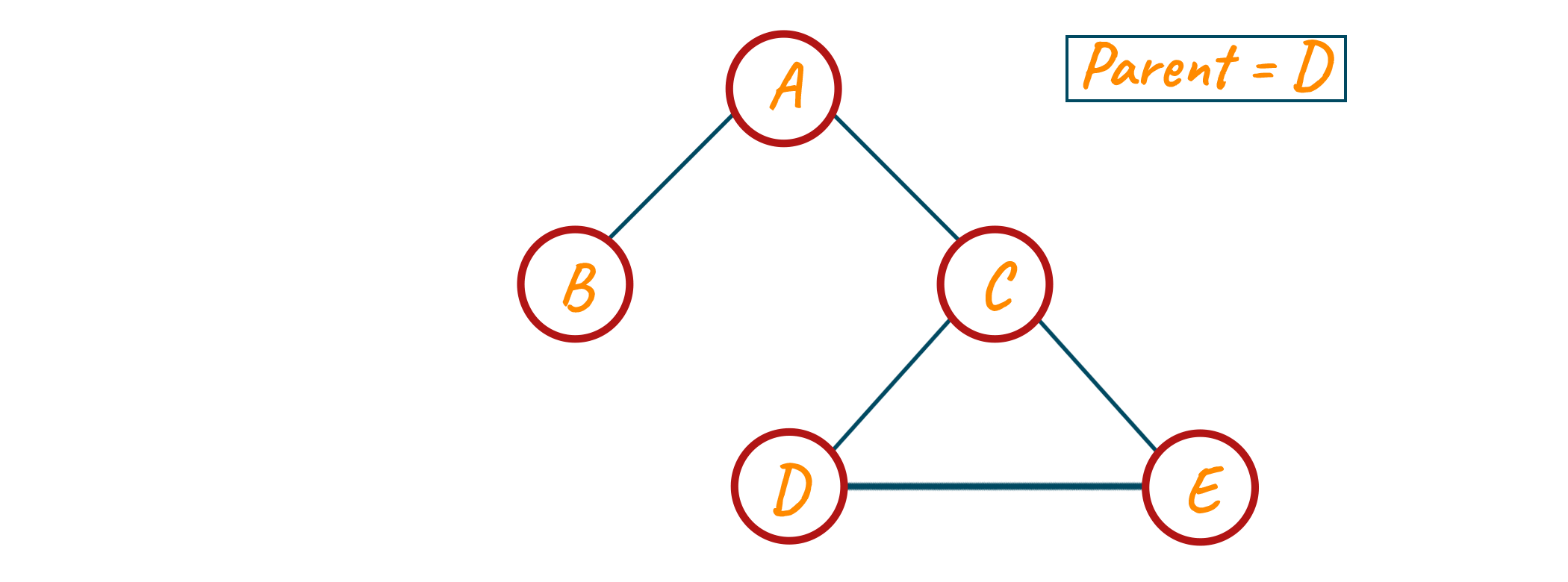
Now from node E, we have a neighbor i.e., node D which is visited but the parent of node E, and another is node C which is visited but is not a parent of node E.

Since this was the condition we discussed in the above theory, we can say that we have detected a cycle i.e., C-D-E-C. 

Algorithm to Detect Cycle in an Undirected Graph

Here is the algorithm we will use to detect a cycle in an undirected graph:

Assign the source_vertex to visited
    for all the adjacent_vertices to the source_vertex do
        if the adjacent_vertex is not visited, then
            Assign parent [ adjacent_vertex ] = source_vertex
            detect_cycle (adjacent_vertex)
        else if the parent [ source_vertex ] != adjacent_vertex, then
            cycle detected 
     return

Check out the implementation of the DFS approach to detect cycles in undirected graphs using Python programming:

Python Implementation

Below we have given the complete code to check if an undirected graph has a cycle or not, using Python code:

class Graph:
 
    def __init__(self, edges, a):
 
        # Adjacency list representation
        self.adjacencyList = [[] for _ in range(a)]
 
        for (source, destination) in edges:
            self.adjacencyList[source].append(destination)
            self.adjacencyList[destination].append(source)
 
 
# Function for DFS_Traversal traversal
def DFS_Traversal(graph, v, visited, parent_node=-1):
 
    # assign current node as
    visited[v] = True
 
    # loop for every edge (v, u)
    for u in graph.adjacencyList[v]:
 
        # if `u` is not visited
        if not visited[u]:
            if DFS_Traversal(graph, u, visited, v):
                return True
 
        # if `u` is visited, and `u` is not a parent_node
        elif u != parent_node:
            # found a back-edge 
            return True
 
    # No back-edges were found 
    return False
 
 
if __name__ == '__main__':
 
    # List of graph edges
    edges = [
        (0, 1), (0, 2), (2, 3), (2, 4), (3, 4)
    ]
 
    # number of nodes in the graph
    a = 5
 
    # construct graph
    constructed_graph = Graph(edges, a)
 
    # note the visited and unvisited nodes
    visited = [False] * a
 
    # perform DFS traversal from source_node
    if DFS_Traversal(constructed_graph, 0, visited):
        print('Cycle detected')
    else:
        print('Cycle not detected')

Output:

Cycle detected

Time Complexity

The time complexity of using the DFS approach is O(V+E), where V is the number of vertices and E is the number of edges in the given graph.

Can we use BFS to Detect Cycles in an Undirected Graph?

A graph traversal technique called BFS (breadth-first search) initially searches all the vertices that are equally far from the beginning vertex before going on to the vertices that are farther away. In an undirected graph, it can be used to find cycles.

Maintaining a parent array that retains the parent node of each visited node throughout the traversal is the fundamental concept underlying utilizing BFS to find cycles in an undirected graph. There is a cycle in the network if we come across a visited node that's got a parent distinct from the present node.

View the BFS algorithm for an undirected graph to find cycles:

from typing import List
from queue import Queue

def isCyclicBFS(graph: List[List[int]], start: int) -> bool:
    visited = [False] * len(graph)
    parent = [-1] * len(graph)
    q = Queue()
    visited[start] = True
    q.put(start)
    while not q.empty():
        curr = q.get()
        for neighbor in graph[curr]:
            if not visited[neighbor]:
                visited[neighbor] = True
                parent[neighbor] = curr
                q.put(neighbor)
            elif parent[curr] != neighbor:
                return True
    return False

A graph that can be represented in an adjacency list and a start vertex for the BFS traversal are the inputs for the isCyclicBFS function. It sets up two vectors, visited and parent, to keep a record of the visited nodes and their parents, respectively. Additionally, it adds the initial vertex to the queue q after initializing it.

Once in a loop, the function stays in it until the waiting list is empty. The first element is taken out of the queue and its neighboring vertices are looked at during every iteration of the loop. 

Also, learn how to detect cycles in a directed graph here.

Conclusion

Competitive problems play an important role in testing any candidate's knowledge during technical interviews. The graph is one such critical data structure to deal with, and therefore, this article explores the problem of detecting cycles in undirected graphs using the DFS algorithm in Python.