Kosaraju's Algorithm to Find Strongly Connected Components

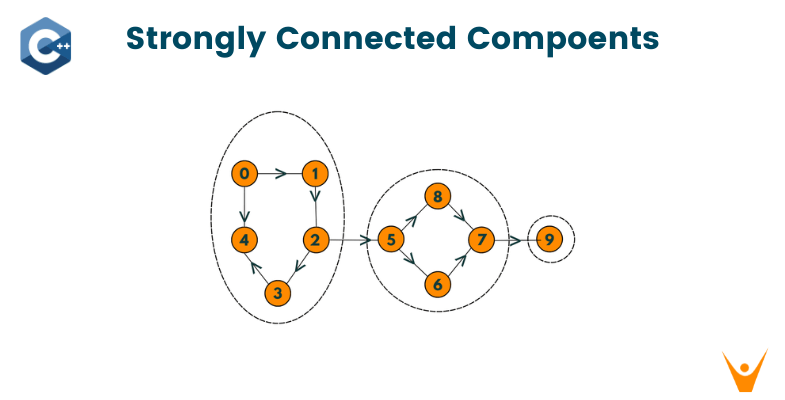
Graphs are one of the most important topics you need to master before any technical interview. In this article, you will learn about the strongly connected components in a graph, and Kosaraju's Algorithm to find them in a graph.

What are Strongly Connected Components?

In a directed graph, a strongly connected component is a subset of vertices in which every vertex is reachable from every other vertex.

Technically, we can define it as a maximal subset of vertices S in which for every pair of vertices u and v in S, there exists a path from u to v and a path from v to u. So, we can say that it is a group of vertices that are "tightly connected" to each other.

A strongly connected component or SCC can help determine which parts of a directed graph are reachable from specific starting points. 

The key difference between connected components and strongly connected components is the type of paths that we use to travel between vertices. In a connected component, we use undirected paths, while in a strongly connected component, we use directed paths.

Let us understand the concept with an example. Consider the example given below:

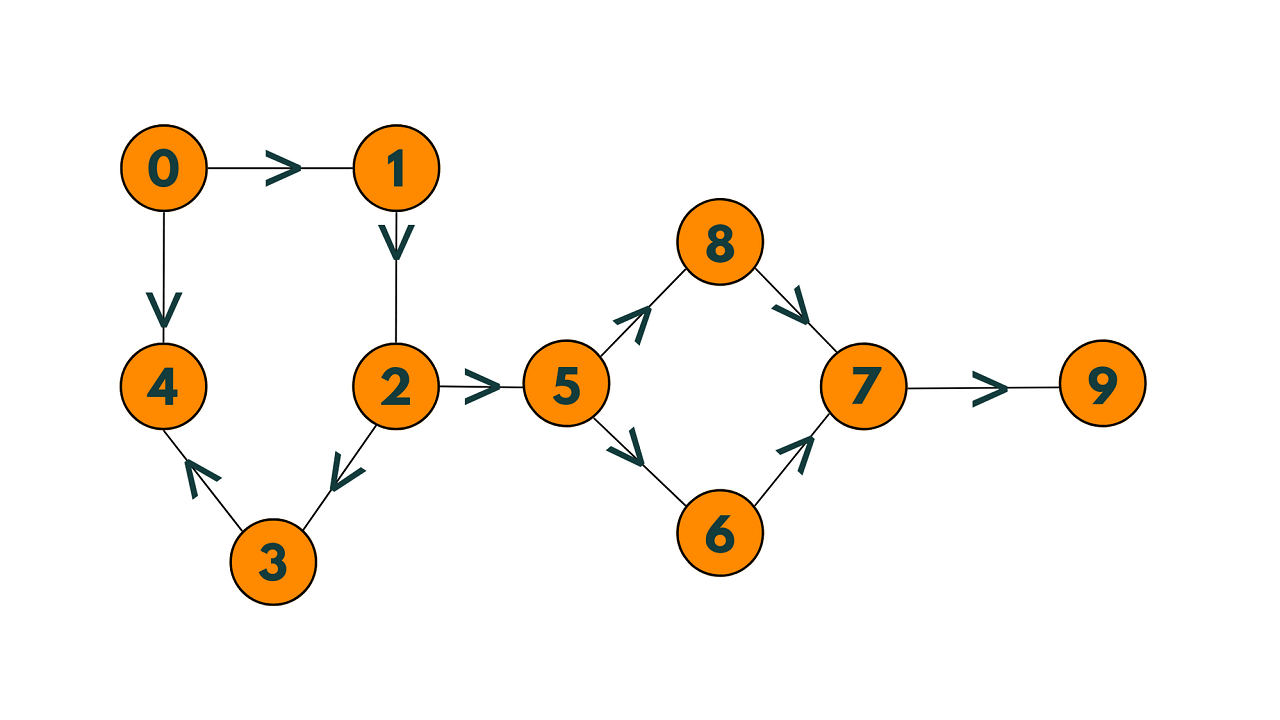
The following elements in the graph above are closely connected:

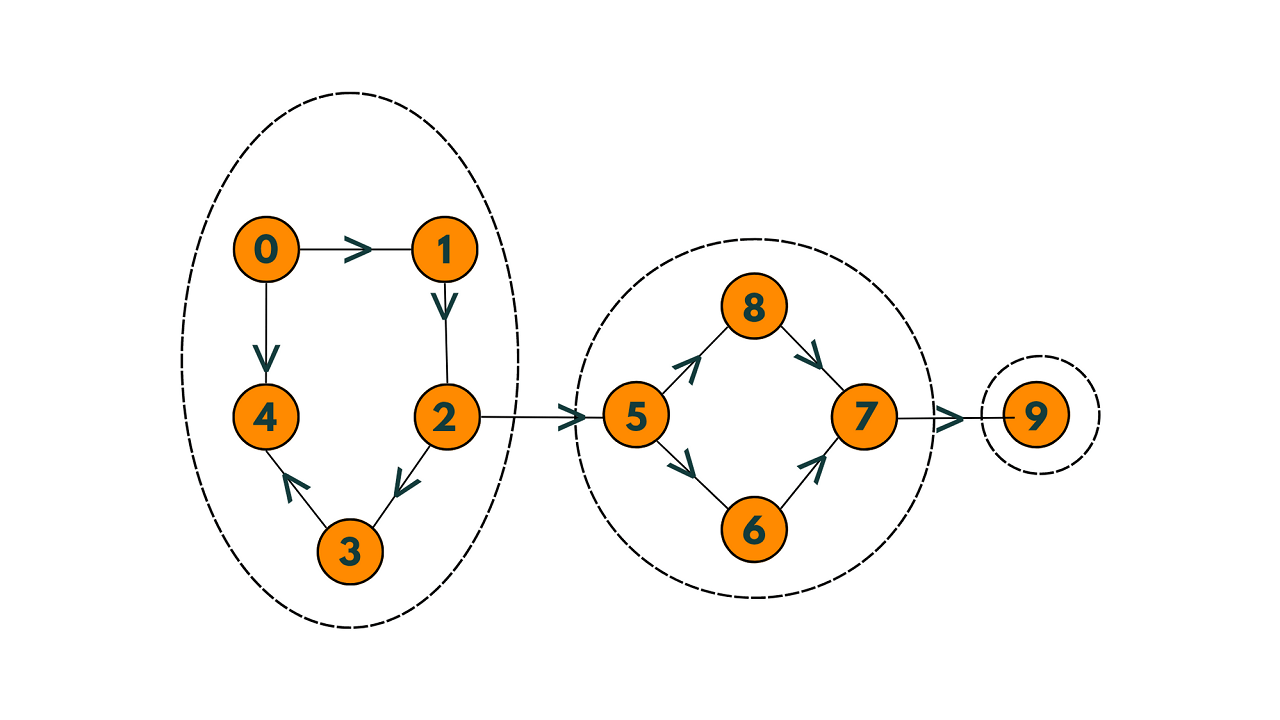
Every vertex in the first strongly connected component can reach every other vertex via a directed path, as can be seen.

One common algorithm to find strongly connected components in a directed graph is Kosaraju's algorithm, which uses two depth-first searches to explore the graph and identify strongly connected components. Let's take a look at Kosaraju's algorithm.

What is Kosaraju's Algorithm?

Kosaraju's algorithm is used in graph theory for finding strongly connected components in directed graphs.

Kosaraju's algorithm works by performing two depth-first searches on the graph. The first pass creates a reverse graph by reversing the direction of all edges in the original graph. The second pass performs a depth-first search on the reverse graph, starting at a node that has not been visited in the first pass. The result of the second pass is a set of strongly connected components. 

However, it is not the most efficient algorithm for this task since it is designed specifically for directed graphs. 

Here are the high-level steps for Kosaraju's algorithm:

1. Perform a depth-first search on the graph and push each vertex onto a stack in the order in which it finishes its recursive calls.
2. Reverse the direction of each edge in the graph to obtain a new, "reversed" graph.
3. Pop vertices off the stack one by one and perform a depth-first search on the reversed graph starting at each vertex that has not been visited yet. Each depth-first search will identify a strongly connected component.
4. Return the set of strongly connected components.

Check the pseudocode below to implement it:

function kosaraju(G):
    # Step 1: Create an empty stack and mark all vertices as unvisited.
    stack = []
    visited = set()
    
    # Step 2: For each unvisited vertex in the graph, perform a depth-first search.
    for vertex in G.vertices:
        if vertex not in visited:
            dfs_pass_one(G, vertex, stack, visited)
    
    # Step 3: Create a reverse graph by reversing the direction of all edges.
    reverse_G = reverse_graph(G)
    
    # Step 4: Pop vertices from the stack and perform a depth-first search on the reverse graph.
    visited.clear()
    strongly_connected_components = []
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            scc = []
            dfs_pass_two(reverse_G, vertex, visited, scc)
            strongly_connected_components.append(scc)
    
    # Step 5: Return the set of strongly connected components.
    return strongly_connected_components

function dfs_pass_one(G, vertex, stack, visited):
    visited.add(vertex)
    for neighbor in G.neighbors(vertex):
        if neighbor not in visited:
            dfs_pass_one(G, neighbor, stack, visited)
    stack.append(vertex)

Note that this pseudocode assumes that the graph is represented as an adjacency list or matrix and that the 'Graph' class has methods for adding vertices and edges, and for retrieving a vertex's neighbors.

Additionally, dfs_pass_one  and dfs_pass_two functions perform the depth-first searches for the first and second passes of the algorithm, respectively. The reverse_graph function creates a reverse graph by iterating over the vertices and edges of the original graph and reversing the direction of each edge.

C++ Implementation

Below is the C++ code to implement Kosaraju's algorithm:

#include 
#include 
#include 
using namespace std;

void dfs_pass_one(vector<vector<int>>& graph, int vertex, stack<int>& stack, vector<bool>& visited) {
    visited[vertex] = true;
    for (int neighbor : graph[vertex]) {
        if (!visited[neighbor]) {
            dfs_pass_one(graph, neighbor, stack, visited);
        }
    }
    stack.push(vertex);
}

void dfs_pass_two(vector<vector<int>>& graph, int vertex, vector<bool>& visited, vector<int>& scc) {
    visited[vertex] = true;
    scc.push_back(vertex);
    for (int neighbor : graph[vertex]) {
        if (!visited[neighbor]) {
            dfs_pass_two(graph, neighbor, visited, scc);
        }
    }
}

vector<vector<int>> kosaraju(vector<vector<int>>& graph) {
    // Step 1: Create an empty stack and mark all vertices as unvisited.
    stack<int> stack;
    vector<bool> visited(graph.size(), false);

    // Step 2: For each unvisited vertex in the graph, perform a depth-first search.
    for (int vertex = 0; vertex < graph.size(); vertex++) {
        if (!visited[vertex]) {
            dfs_pass_one(graph, vertex, stack, visited);
        }
    }

    // Step 3: Create a reverse graph by reversing the direction of all edges.
    vector<vector<int>> reverse_graph(graph.size());
    for (int vertex = 0; vertex < graph.size(); vertex++) {
        for (int neighbor : graph[vertex]) {
            reverse_graph[neighbor].push_back(vertex);
        }
    }

    // Step 4: Pop vertices from the stack and perform a depth-first search on the reverse graph.
    visited.assign(graph.size(), false);
    vector<vector<int>> strongly_connected_components;
    while (!stack.empty()) {
        int vertex = stack.top();
        stack.pop();
        if (!visited[vertex]) {
            vector<int> scc;
            dfs_pass_two(reverse_graph, vertex, visited, scc);
            strongly_connected_components.push_back(scc);
        }
    }

    // Step 5: Return the set of strongly connected components.
    return strongly_connected_components;
}

int main() {
    // Example usage
    vector<vector<int>> graph = {{1}, {2}, {0}, {1, 3}, {2}};
    vector<vector<int>> scc = kosaraju(graph);
    for (auto& component : scc) {
        cout << "Strongly connected component: ";
        for (int vertex : component) {
            cout << vertex << " ";
        }
        cout << endl;
    }
    return 0;
}

Output:

Strongly connected component: 4 
Strongly connected component: 3 
Strongly connected component: 0 2 1 

Note that this implementation uses recursion for the depth-first searches and the vector data structure is used to represent the graph and the set of strongly connected components.

Time Complexity

The Time Complexity of Kosaraju's algorithm is O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because the algorithm performs two depth-first searches on the graph, each taking O(V + E) time. In addition, creating the reverse graph takes O(V + E) time since each edge needs to be reversed.

Does the Kosaraju Algorithm work for Undirected Graphs?

No, Kosaraju's algorithm does not work for undirected graphs. The algorithm relies on the directionality of edges which only applies to directed graphs.

In an undirected graph, there is no "direction" with edges. To find connected components in an undirected graph, you can use other algorithms such as DFS or BFS. These algorithms can traverse the entire undirected graph, exploring all connected regions and identifying the different connected components in the process. 

Conclusion

Strongly connected components are widely used in network analysis to identify sub-networks that are more tightly connected than the rest of the network as well as in algorithm design and data compression. You now know how to find Strongly Connected Components in a graph with its C++ code.