Climbing Stairs Problem (with C++, Java & Python code)

In interviews and coding contests, indirect questions will be asked about the known concepts. In this article, we are going to discuss the Climbing Stairs Problem. The problem might seem new but the logic is quite familiar even for the beginner.

What is the Climbing Stairs Problem?

The ascending stairs issue asks how many different ways there are to ascend a staircase. It is a classic problem in computer science.

The issue can be stated in the following way: Assume you are ascending an n-step staircase. Either one or two steps can be taken at once. How many different ways can you ascend the staircase? Numerous methods, such as the Fibonacci number approach and the brute force method, can be used to solve this issue. 

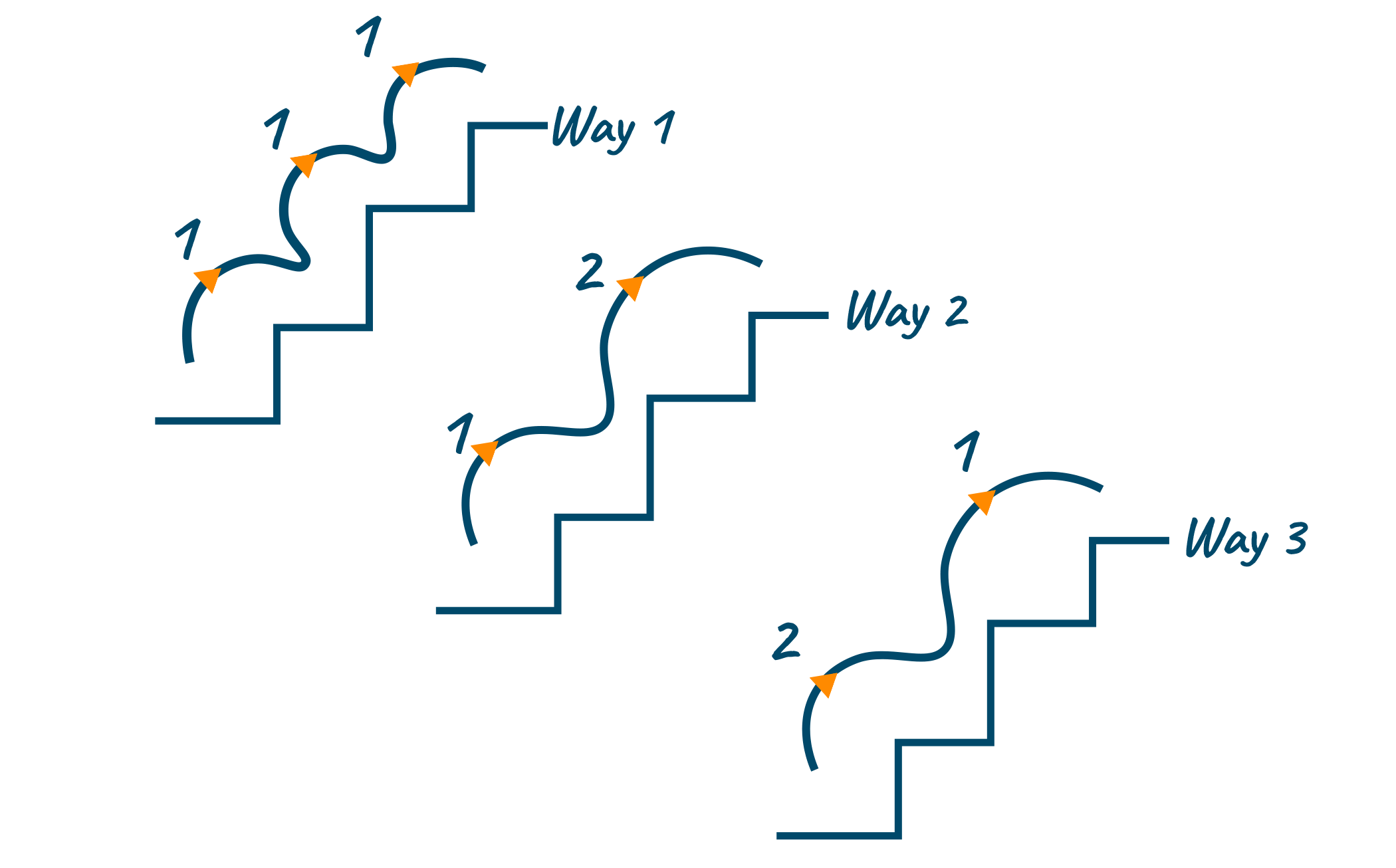
Here is the problem statement: "Consider you are climbing a staircase. It takes n steps to reach the top. Each time you can either climb 1 or 2 steps. We have to find how many distinct ways can you climb to the top."

Sample Input: n = 3

Sample Output: 3

(Way 1: 1->1->1, Way 2: 2->1, Way 3: 1->2)

Solving Climbing Stairs Problem

Before we discuss the solution to this problem, let's discuss dynamic programming. It is a technique that divides the problem into parts, finds a solution at each stage, and stores it for future use. It is used to get an optimized solution with the concept of reusing the stored solutions of the sub-parts.

The primary use of dynamic programming is to reduce time complexity. We can solve recursive problems with dynamic programming. It will reduce the time complexity from exponential to linear.

Let's try to solve this climbing stairs problem with the help of dynamic programming.

Algorithm & Example

The algorithm for Climbing stairs is exactly similar to the Fibonacci series.

1. Let n be the number of stairs. If n <=0, then the number of ways to climb the staircase should be zero.
2.  If n == 1, then there is only one way to climb the stair.
3. For the numbers greater than 1, we can simply find the solution by adding previous steps i.e., dp[n-1] + dp[n-2]. Create a new array and store the output at each step.
4. Then finally return the last value in the array as the output.

Let's also take an example to better understand it.

Consider the value of n is 3. There are 3 ways to reach the top. We use a dynamic programming approach for this problem. We create a new array of steps that store the value at each step. Let us first initialize steps[0] = 1 and steps[1] = 1, then to find steps[2] we have to add previous two values i.e., steps[0] + steps[1] which is 1+1 = 2.

Then to find steps[3] we have to add the previous two values i.e., steps[1] + steps[2] which is 1+2 = 3. Now we know that steps[n] are the final output, hence steps[3] value i.e. 3 is the required number of ways to climb the stairs. The explanation is illustrated in the following diagram.

Java Implementation

Here is the Java code to solve Climbing Stairs Problem using dynamic programming:

class Solution {
 public static int climbStairs(int n) {
  if(n<=0){
   return 0;
  }
  else if (n == 1) {
   return 1;
  }
  else{
   int[] steps = new int[n + 1];
   steps[0] = 1;
   steps[1] = 1;
   for (int i = 2; i <= n; i++) {
   steps[i] = steps[i - 2] + steps[i - 1];
   }
  }
 return steps[n];
 }
 public static void main(String[] args) {
  int n=3;
  System.out.println(climbStairs(n));
 }
}

Output:

3

C++ Implementation

Here is the C++ program to solve Climbing Stairs Problem using dynamic programming:

#include<iostream>
using namespace std;
int climbStairs(int n) {
 if(n<=0){
  return 0;
 }
 else if (n <= 1) {
  return 1;
 }
 else{
  int steps[n+1];
  steps[0] = 1;
  steps[1] = 1;
  for (int i = 2; i <= n; i++) {
   steps[i] = steps[i - 2] + steps[i - 1];
  }
 }
 return steps[n];
}
int main(){
 int n=3;
 cout<<climbStairs(n);
 return 0;
}

Output:

3

Python Implementation

Here is the Python code to solve Climbing Stairs Problem:

def climbStairs(n):
 steps = []
 steps.append(1)
 steps.append(2)
 for i in range(2, n):
  steps.append(f[i - 1] + f[i - 2])
 return steps[n - 1]
n=3
print(climbStairs(n))

Output:

3

Time & Space Complexity

We are iterating through a single loop to find a number of ways to climb the stairs. Hence the time complexity will be O(n), where n is the number of stairs.

In this approach of storing the values using dynamic programming, we are creating a new array. Hence the space complexity for this solution will be O(n), where n is the number of stairs.

Brute Force Approach

The climbing stairs problem can be solved brute forcibly by iterating through all combinations of both one and two steps which can be taken at each stairway step until the overall amount of steps equals n. The number of options that provide a total of n steps is the solution to the puzzle.

The code for the brute force method is as follows:

def climbStairsBruteForce(n):
    if n == 0 or n == 1:
        return 1
    return climbStairsBruteForce(n-1) + climbStairsBruteForce(n-2)

The function climbStairsBruteForce, which accepts the integer n as input along with returns the number of unique methods to ascend a staircase with n steps, is defined in the code above. In order to determine whether there is only one different method to climb the staircase (either by taking 0 steps or 1 step), the function first determines whether n is equal to 0 or 1.

If not, the function recursively uses the inputs n-1 and n-2 to call itself, returning the sum of the two outcomes. When every possible combination of steps is taken into account, the worst-case temporal complexity of this technique is O(2n). Because of this, it is not feasible for big values of n.

Fibonacci Number Approach

The number of unique ways to ascend a staircase having n steps is equal to the n-th Fibonacci number, which forms the basis of the Fibonacci number approach to resolving the ascending stairs problem. Starting with 0 and 1, the Fibonacci sequence is a set of numbers where each number equals the sum of the two before it. The order is as follows: 0; 1; 2; 3; 5; 8; 13; 21; 34; 55; and so on.

The code for using the Fibonacci numbers is as follows:

def climbStairsFibonacci(n):
    if n == 0 or n == 1:
        return 1
    first = 1
    second = 2
    for i in range(3, n+1):
        third = first + second
        first = second
        second = third
    return second

In the code above, a function called climbStairsFibonacci is defined. It accepts an integer n for input it returns the number of unique methods there are to ascend a staircase having n steps. In order to determine whether there is just one distinct way to climb the staircase (either by taking 0 steps or 1 step), the function first determines whether n is equal to 0 or 1.

If not, the function uses the first, second, and third variables to repeatedly calculate the n-th Fibonacci number. The loop iterates from i=3 to i=n, computing the third variable when the sum of the first two, and updating the first and second variables' values as necessary.

Conclusion

Dynamic programming is an important concept to be covered for any interview or competitive programming. There are many ways you can try to solve thr Climbing Stairs Problem so you will have a good understanding of the concepts.