The "children sum property" is a mathematical concept that is often taught to children in primary school. In this article, we will explore what the children's sum property is and how it is used.
Children Sum Property in Binary Tree
As you know, a binary tree is a tree structure in which each node has at most two children, referred to as the left child and the right child. A binary tree is said to satisfy the "children sum property" to determine it is a valid tree or not.
The Children Sum Property is a property of a binary tree where the sum of the values of its left and right children is equal to the value of the node itself.
It is important because it helps to ensure that a binary tree is well-formed. If this property is violated for any node in the tree, then the tree is not well-formed, and there is likely an error in the construction of the tree.
Let's understand it with an example. Consider the following binary tree:
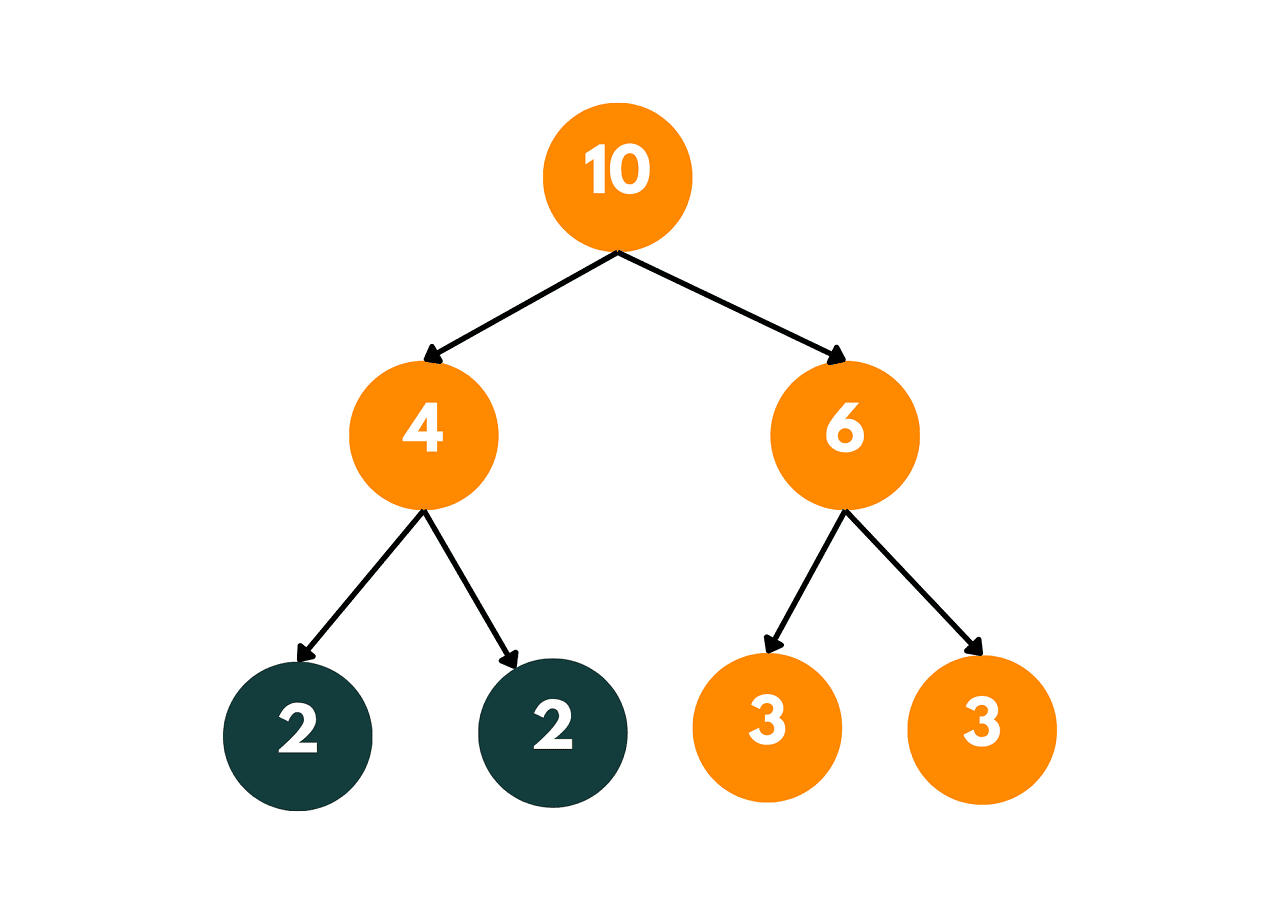
In this binary tree, the root node has a value of 10, and its left and right children have values of 4 and 6, respectively. The sum of the values of the left and right children is equal to the value of the root node, i.e., 4 + 6 = 10, which satisfies the 'children sum property'.
Similarly, the left child of the root node has two children with values 2 and 2, and their sum is 4, which is equal to the value of the left child. The right child of the root node also has two children with values 3 and 3, and their sum is 6, which is equal to the value of the right child. Thus, the children sum property is satisfied for all the nodes in this binary tree.
This example demonstrates that the children sum property holds for a binary tree where the value of each node is equal to the sum of the values of its left and right children. The property can also hold for other binary trees where the sum of the values of the left and right children is equal to the value of the parent node.
Algorithm to Check for Children Sum Property
The Children Sum Property can also be used to construct a binary tree given its inorder and level order traversals. In this case, we can use the following algorithm:
- Create an empty queue.
- Push the root node onto the queue.
- While the queue is not empty, do the following: a. Pop the first node from the queue. b. If the inorder traversal array has elements remaining, create a new node with the next element in the inorder traversal array and set it as the left child of the popped node. c. If the inorder traversal array has elements remaining, create a new node with the next element in the inorder traversal array and set it as the right child of the popped node. d. Push the left and right children onto the queue.
- Return the root node.
Let's take a look at the pseudocode for checking the children sum property for a binary tree:
function isChildrenSumPropertySatisfied(node):
if node is NULL, return true
# If node is a leaf node
if node.left is NULL and node.right is NULL:
return true
# If node has only one child
if node.left is NULL:
return (node.value == node.right.value) AND isChildrenSumPropertySatisfied(node.right)
if node.right is NULL:
return (node.value == node.left.value) AND isChildrenSumPropertySatisfied(node.left)
# If node has two children
return (node.value == node.left.value + node.right.value) AND isChildrenSumPropertySatisfied(node.left) AND isChildrenSumPropertySatisfied(node.right)
The above pseudo-code is a recursive function that takes a node as input and returns true if the children sum property is satisfied for the given node and its children. The function checks if the node has one or two children and calculates their sum accordingly.
If the sum is equal to the value of the node, the function checks if the children sum property is satisfied for the left and right subtrees recursively. Finally, the function returns true if all the conditions are satisfied, and false otherwise.
Check for Children Sum Property using Recursion
Here's a C++ implementation of the children sum property for a binary tree using recursion:
#include<bits/stdc++.h> using namespace std; // Define the structure of a binary tree node struct Node { int data; Node *left, *right; Node(int data) { this->data = data; left = right = NULL; } }; // Function to check if the children sum property holds for a given binary tree bool isChildrenSumPropertySatisfied(Node* root) { // If the node is NULL or if it is a leaf node, then the property holds trivially if (root == NULL || (root->left == NULL && root->right == NULL)) { return true; } // Recursively check the property for the left and right subtrees if (isChildrenSumPropertySatisfied(root->left) && isChildrenSumPropertySatisfied(root->right)) { int left_data = (root->left != NULL) ? root->left->data : 0; int right_data = (root->right != NULL) ? root->right->data : 0; // Check if the property holds for the current node return (root->data == left_data + right_data); } // If the property does not hold for any subtree, then it does not hold for the current node return false; } int main() { // Create a binary tree Node* root = new Node(10); root->left = new Node(8); root->right = new Node(2); root->left->left = new Node(3); root->left->right = new Node(5); // Check if the children sum property holds for the binary tree if (isChildrenSumPropertySatisfied(root)) { cout << "Children sum property holds for the binary tree." << endl; } else { cout << "Children sum property does not hold for the binary tree." << endl; } return 0; }
Output:
Children sum property holds for the binary tree.
The tree that we constructed in the above code is given below:
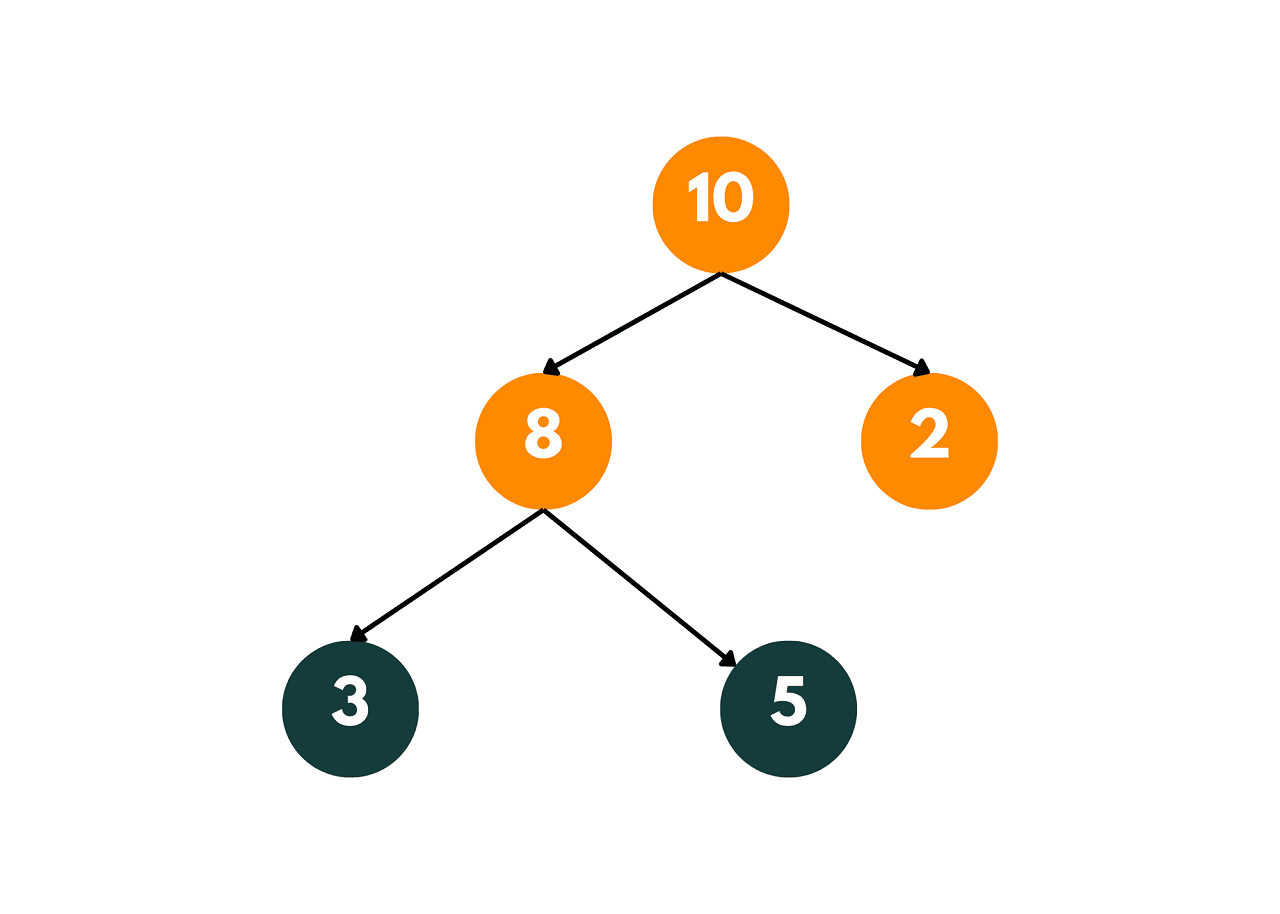
In this code, we first check if the given node is NULL or a leaf node. If so, the property holds trivially. Otherwise, we recursively check the property for the left and right subtrees and compute the sum of the values of their root nodes.
Finally, we check if the sum of the left and right subtree roots is equal to the value of the current node. If the property holds for all the nodes in the tree, the function returns true, otherwise, it returns false.
The time complexity of this implementation is O(n), where n is the number of nodes in the binary tree. The space complexity is O(h), where h is the height of the binary tree, as the maximum space used by the recursion stack is equal to the height of the tree. You should learn more about Recursion in C++ as well.
However, there is another way to check whether the binary tree holds the child sum property. Let's further take a look at it.
Check for Children Sum Property using Deque
Here's a C++ implementation of the children sum property for a binary tree using deque:
#include<iostream> #include<deque> using namespace std; // define the structure of a binary tree node struct Node { int data; Node* left; Node* right; Node(int val) { data = val; left = nullptr; right = nullptr; } }; // check if the children sum property holds for a binary tree bool isChildrenSumPropertySatisfied(Node* root) { if (!root) { return true; // empty tree satisfies property } deque<Node*> dq; dq.push_back(root); // add root to deque while (!dq.empty()) { int dq_size = dq.size(); // number of nodes at current level int level_sum = 0; // sum of node values at current level for (int i = 0; i < dq_size; i++) { Node* node = dq.front(); dq.pop_front(); // remove the first node from the deque level_sum += node->data; // add the current node value to level sum if (node->left) { dq.push_back(node->left); // add the left child to the deque } if (node->right) { dq.push_back(node->right); // add the right child to the deque } } if (level_sum != 0 && level_sum != dq_size * (dq_size + 1) / 2) { return false; // check if the sum of node values at the current level satisfies the property } } return true; // children sum property holds for the binary tree } int main() { // create a binary tree Node* root = new Node(10); root->left = new Node(8); root->right = new Node(2); root->left->left = new Node(3); root->left->right = new Node(5); root->right->left = new Node(1); // check if the children sum property holds for the binary tree if (isChildrenSumPropertySatisfied(root)) { cout << "Children sum property holds for the binary tree." << endl; } else { cout << "Children sum property does not hold for the binary tree." << endl; } return 0; }
Output:
Children sum property does not hold for the binary tree.
The tree that we constructed in the above code is given below:
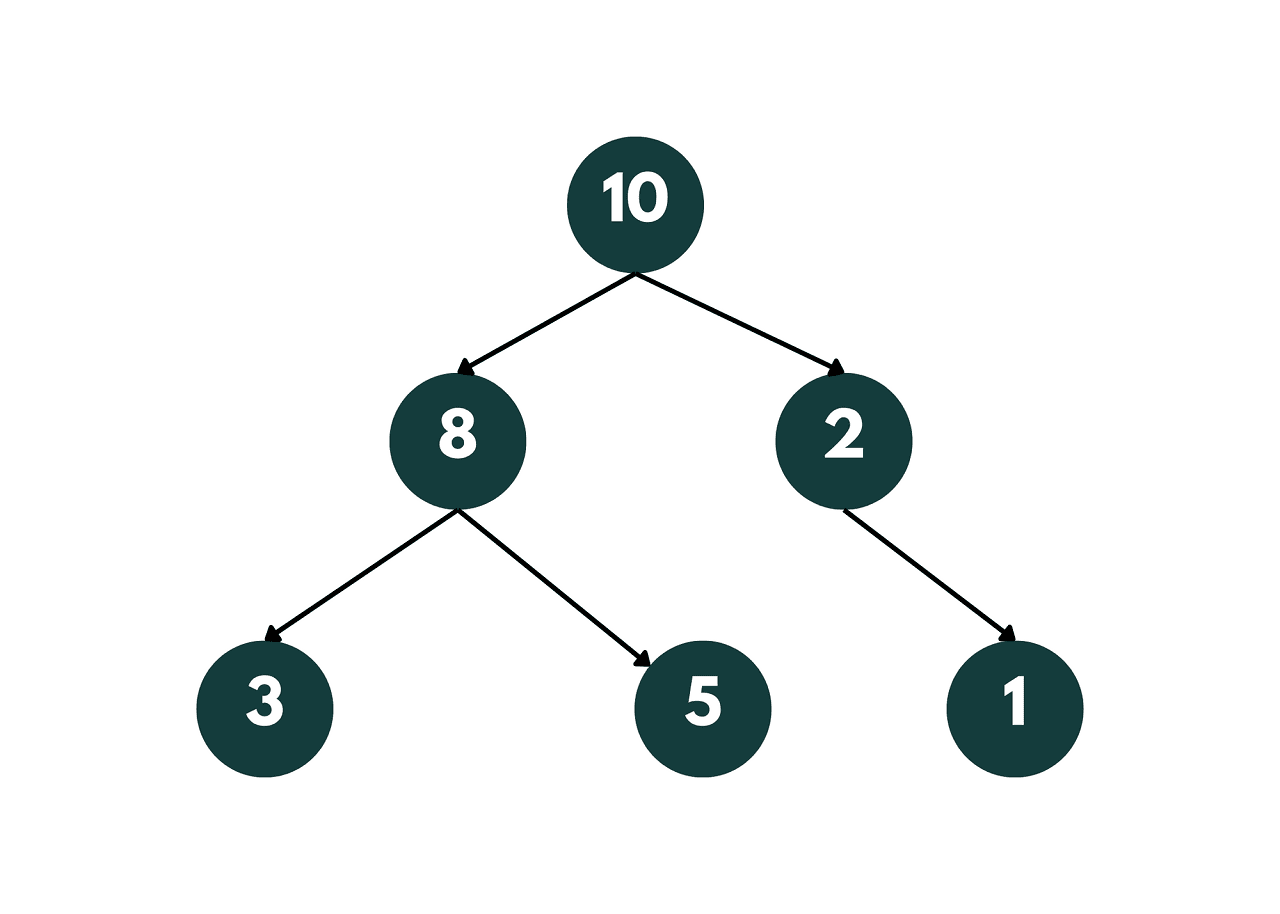
In this implementation, we use a deque to keep track of the nodes at each level of the binary tree. We start by adding the root node to the deque and then iterate over the nodes at each level of the tree until the deque becomes empty.
For each level, we compute the sum of node values and check if it satisfies the children sum property. If the property holds for all levels of the tree, the function returns true, otherwise, it returns false.
The time complexity of this implementation is O(n), where n is the number of nodes in the binary tree, as we visit each node exactly once.
The space complexity is O(w), where w is the maximum width of the binary tree, as we store at most w nodes in the deque at any given time. In the worst case, where the binary tree is a complete binary tree, the width is O(n/2), and hence the space complexity is O(n).
Conclusion
The children sum property is a useful property of binary trees that has several applications. It can be used to test the correctness of algorithms that operate on binary trees. By checking the property before and after running the algorithm, we can ensure that the algorithm has not introduced any errors in the binary tree.








