BFS in Java: Breadth-first Search Algorithm for Graph (with code)

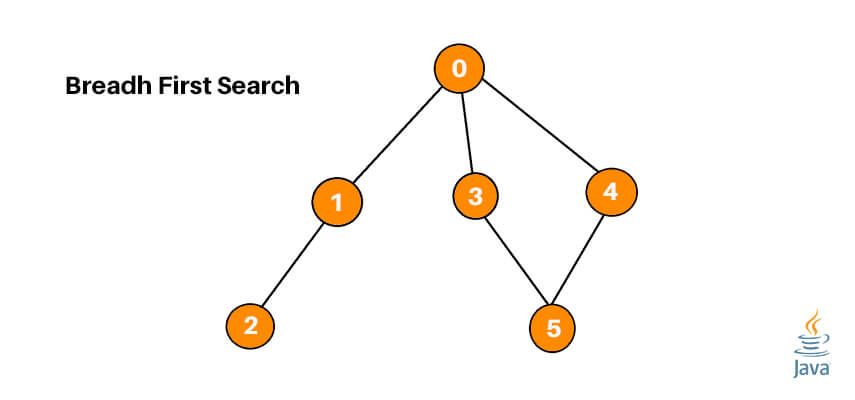
Graph traversal is the process of moving from the root node to all other nodes in the graph. It is done using two main algorithms: Breadth-First Search and Depth-First Search.  In this article, we are going to go over the basics of the BFS algorithm and its implementation with Java code. 

What is a Breadth-First Search in Java?

Breadth-First Search, or BFS, relies on the traversal of nodes by the addition of the neighbor of every node starting from the root node to the traversal queue. BFS for a graph is similar to a tree, the only difference being graphs might contain cycles. Unlike depth-first search, all of the neighbor nodes at a certain depth are explored before moving on to the next level.

BFS Algorithm

The general process of exploring a graph using breadth-first search includes the following steps:

1. Take the input for the adjacency matrix or adjacency list for the graph.
2. Initialize a queue.
3. Enqueue the root node (in other words, put the root node at the beginning of the queue).
4. Dequeue the head (or first element) of the queue, then enqueue all of its neighboring nodes, starting from left to right. If a node has no neighboring nodes which need to be explored, simply dequeue the head and continue the process. (Note: If a neighbor which is already explored or in the queue appears, don’t enqueue it – simply skip it.)
5. Keep repeating this process till the queue is empty.

(In case people are not familiar with enqueue and dequeue operations, enqueue operation adds an element to the end of the queue while dequeue operation deletes the element at the start of the queue.)

BFS Example

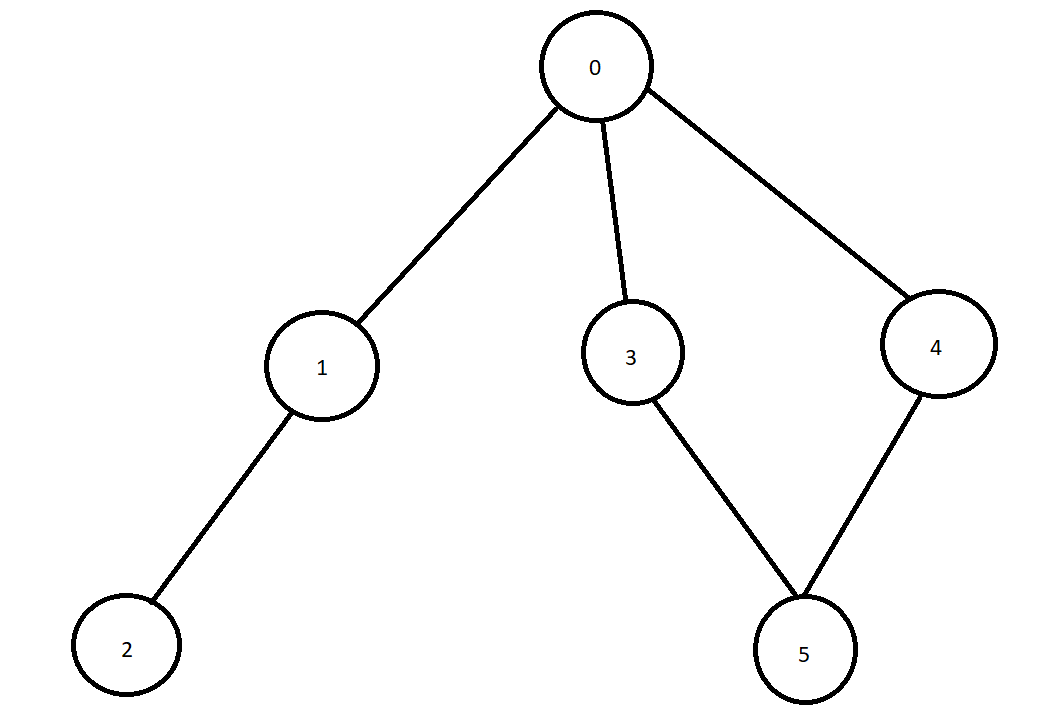
Let’s work with a small example to get started. We are using the graph drawn below, starting with 0 as the root node.

Iteration 1: Enqueue(0).

Queue after iteration 1 :

Iteration 2: Dequeue(0), Enqueue(1), Enqueue(3), Enqueue(4).

Queue after iteration 2:

Iteration 3: Dequeue(1), Enqueue(2).

Queue after iteration 3 :

Iteration 4 : Dequeue(3), Enqueue(5). Since 0 is already explored, we are not going to add 1 to the queue again.

Queue after iteration 4:

Iteration 5: Dequeue(4).

Queue after iteration 5:

Iteration 6: Dequeue(2).

Queue after iteration 6 :

Iteration 7: Dequeue(5).

Queue after iteration 7:

Since the queue is again empty at this point, we will stop the process.

Edge Cases

Now, there’s always the risk that the graph being explored has one or more cycles. This means that there’s a chance of getting back to a node that we have already explored. How do we determine if a node has been explored or not? It’s simple – we simply maintain an array for all the nodes.

The array at the beginning of the process will have all of its elements initialized to 0 (or false). Once a node is explored once, the corresponding element in the array will be set to 1 (or true). We simply enqueue nodes if the value of their corresponding element in the array is 0 (or false).

That’s cool, but there’s still another case to consider while you’re traversing all the nodes of a graph using the BFS. What happens when the graph being provided as input is a disconnected graph? In other words, what happens when the graph has not one, but multiple components which are not connected? It’s simple.

As described above, we will maintain an array for all of the elements in the graph. The idea is to iteratively perform the BFS algorithm for every element of the array which is not set to 1 after the initial run of the BFS algorithm is completed. This is even more relevant in the case of directed graphs because of the addition of the concept of “direction” of traversal.

Implementing Breadth-First Search in Java

There are multiple ways of dealing with the code. Here, we would primarily be sharing the process to Implement BFS in Java. Graphs can be stored either using an adjacency list or an adjacency matrix – either one is fine. In our code, we will be using the adjacency list for representing our graph.

It is much easier to work with the adjacency list for implementing the Breadth-First Search algorithm in Java as we just have to move through the list of nodes attached to each node whenever the node is dequeued from the head (or start) of the queue.

The graph used for the demonstration of the code will be the same as the one used for the above example. The implementation is as follows:

import java.io.*;
import java.util.*;

class Graph
{
    private int V;                              //number of nodes in the graph
    private LinkedList<Integer> adj[];              //adjacency list
    private Queue<Integer> queue;                   //maintaining a queue
 
    Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i=0; i<v; i++)
        {
            adj[i] = new LinkedList<>();
        }
        queue = new LinkedList<Integer>();
    }

 
    void addEdge(int v,int w)
    {
        adj[v].add(w);                          //adding an edge to the adjacency list (edges are bidirectional in this example)
    }
 
    void BFS(int n)
    {

        boolean nodes[] = new boolean[V];       //initialize boolean array for holding the data
        int a = 0;
 
        nodes[n]=true;                  
        queue.add(n);                   //root node is added to the top of the queue
 
        while (queue.size() != 0)
        {
            n = queue.poll();             //remove the top element of the queue
            System.out.print(n+" ");           //print the top element of the queue
 
            for (int i = 0; i < adj[n].size(); i++)  //iterate through the linked list and push all neighbors into queue
            {
                a = adj[n].get(i);
                if (!nodes[a])                    //only insert nodes into queue if they have not been explored already
                {
                    nodes[a] = true;
                    queue.add(a);
                }
            }  
        }
    }

    public static void main(String args[])
    {
        Graph graph = new Graph(6);
 
        graph.addEdge(0, 1);
        graph.addEdge(0, 3);
        graph.addEdge(0, 4);
        graph.addEdge(4, 5);
        graph.addEdge(3, 5);
        graph.addEdge(1, 2);
        graph.addEdge(1, 0);
        graph.addEdge(2, 1);
        graph.addEdge(4, 1);
        graph.addEdge(3, 1);
        graph.addEdge(5, 4);
        graph.addEdge(5, 3);
 
        System.out.println("The Breadth First Traversal of the graph is as follows :");
 
        graph.BFS(0);
    }
}

Output:

 The Breadth First Traversal of the graph is as follows :
 0 1 3 4 2 5

Time Complexity of BFS

The running time complexity of the BFS in Java is O(V+E) where V is the number of nodes in the graph, and E is the number of edges.

Since the algorithm requires a queue for storing the nodes that need to be traversed at any point in time, the space complexity is O(V).

Breadth First Search for a Disconnected Graph

You can also implement BFS for a disconnected graph. Here is the code in Java for this purpose:

import java.util.*;

class Graph {
    private int V;
    private LinkedList<Integer>[] adj;

    Graph(int v) {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    void addEdge(int v, int w) {
        adj[v].add(w);
    }

    void BFS(int s, boolean[] visited) {
        LinkedList<Integer> queue = new LinkedList<Integer>();
        visited[s] = true;
        queue.add(s);

        while (queue.size() != 0) {
            s = queue.poll();
            System.out.print(s + " ");

            Iterator<Integer> i = adj[s].listIterator();
            while (i.hasNext()) {
                int n = i.next();
                if (!visited[n]) {
                    visited[n] = true;
                    queue.add(n);
                }
            }
        }
    }

    void BFS_disconnected() {
        boolean[] visited = new boolean[V];
        for (int i = 0; i < V; ++i) {
            if (!visited[i]) {
                BFS(i, visited);
            }
        }
    }

    public static void main(String[] args) {
        Graph g = new Graph(4);
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        System.out.println("Following is Breadth First Traversal " +
                "(starting from vertex 2):");
        g.BFS_disconnected();
    }
}

Output:

Following is Breadth First Traversal (starting from vertex 2):
2 0 1 3

In this code, the Graph class uses an adjacency list to describe an undirected graph. The V property contains the number of vertices in the graph, and the adj property is an array of linked lists, each of which represents the vertices adjacent to a specific vertex.

The addEdge function creates a graph edge between two vertices by adding the second vertex to the linked list for the first.

Starting from a specified vertex s, the BFS technique performs BFS on a single linked component of the graph. It keeps track of which vertices have already been visited by keeping a queue of vertices to be visited and a boolean array visited.

The process begins by tagging s as visited and adding it to the queue. Then it dequeues the next vertex in the queue, publishes its value, and adds all of its unvisited neighbors to the queue again and again. This procedure is repeated until the queue is empty.

The BFS disconnected method applies BFS to all linked graph components. It begins by setting all vertices in a boolean array visited false. Next, it iterates across all vertices, calling the BFS method for each vertex that has not yet been visited to conduct BFS on the corresponding related component.

In the main method, we make a Graph object with four vertices and six edges. Next, starting with vertex 0, we call BFS disconnected to run BFS on all linked components of the graph. The output displays the vertices that were visited during BFS in the order that they were visited.

Also, If you are stuck anywhere with your Java programming, our experts will be happy to provide you with any type of Java homework help.

Applications of BFS

Breadth-First Search has a lot of utility in the real world because of the flexibility of the algorithm. These include:

• Discovery of peer nodes in a peer-to-peer network. 
• Web crawling uses graph traversal for building the index. The process considers the source page as the root node and starts traversing from there to all secondary pages linked with it.
• GPS navigation systems use BFS for finding neighboring locations using the GPS.
• Garbage collection is done with Cheney’s algorithm which utilizes the concept of breadth-first search.
• Algorithms for finding a minimum spanning tree and shortest path in a graph using Breadth-first search.

Conclusion

Graph traversal algorithms like Breadth-first Search or Depth-first Search in Java are some of the most important algorithms that one has to master to get into graphs. Happy Learning :)