Find Largest BST in Binary Tree (with code)

Within the realm of binary trees, one of the most common problems is to find the largest Binary Search Tree contained within it. In this article, we will learn how to find the largest BST in a binary tree using different approaches. Before that, let's revise the basics.

What are Binary Search Trees?

A Binary Search Tree is a specialized type of binary tree in which the value of each node is greater than all values in its left subtree and smaller than all values in its right subtree. The left and right subtrees of a BST are also BSTs themselves, making it a recursive data structure.

Let's consider the following binary tree as an illustrated example:

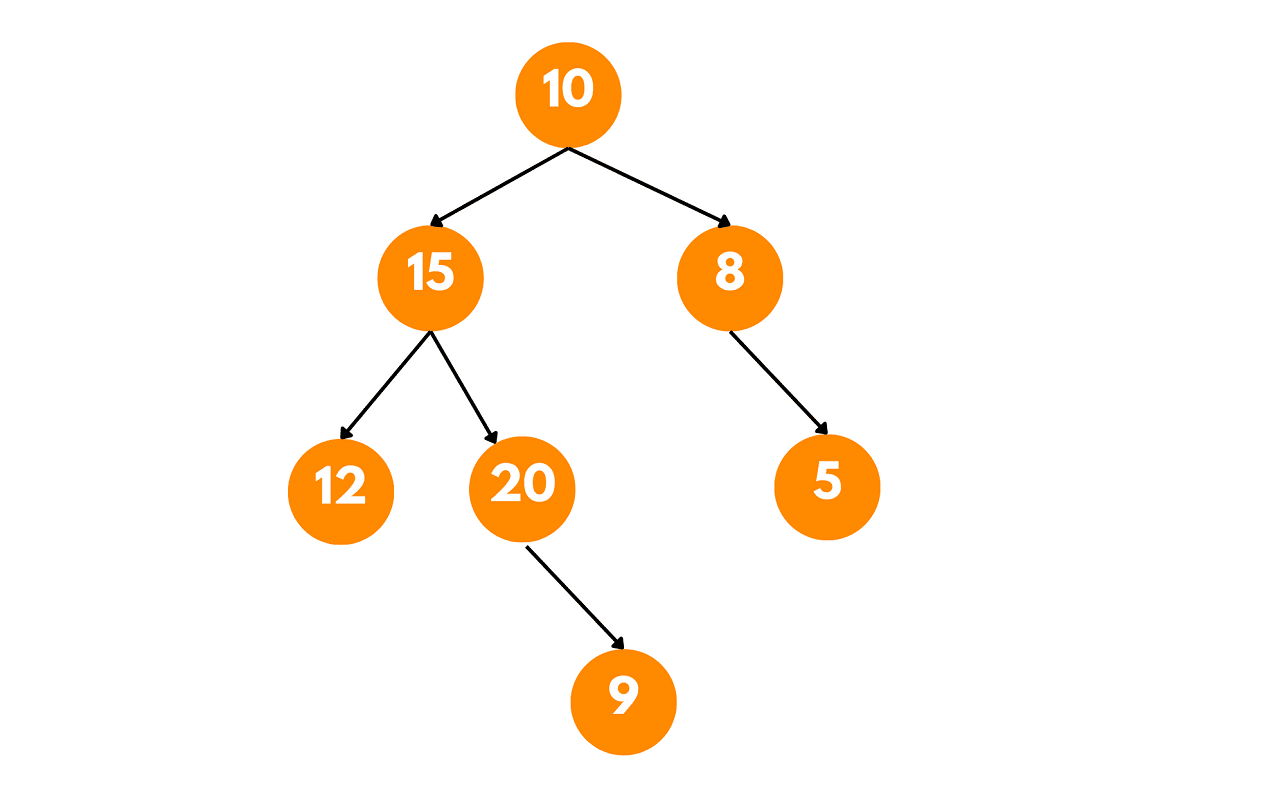
In this binary tree, we will find the largest Binary Search Tree (BST) present.

1. Starting from the root (10), we recursively traverse the left and right subtrees.
2. We check if each subtree is a BST or not by comparing the values of each node with the minimum and maximum values of its respective subtrees.
3. At node 15, we compare its value with the minimum and maximum values of its left subtree (12) and right subtree (20). Since 15 is greater than 12 and less than 20, this subtree is a valid BST.
4. At node 8, we compare its value with the minimum and maximum values of its right subtree (5). Since 8 is greater than 5, this subtree is also a valid BST.
5. At node 5, we compare its value with the minimum and maximum values of its right subtree (9). Since 5 is less than 9, this subtree is not a valid BST.
6. As the subtree rooted at 5 is not a valid BST, we discard it.
7. Finally, we have identified the largest BST in the binary tree. It is the subtree rooted at node 15, with the following structure:

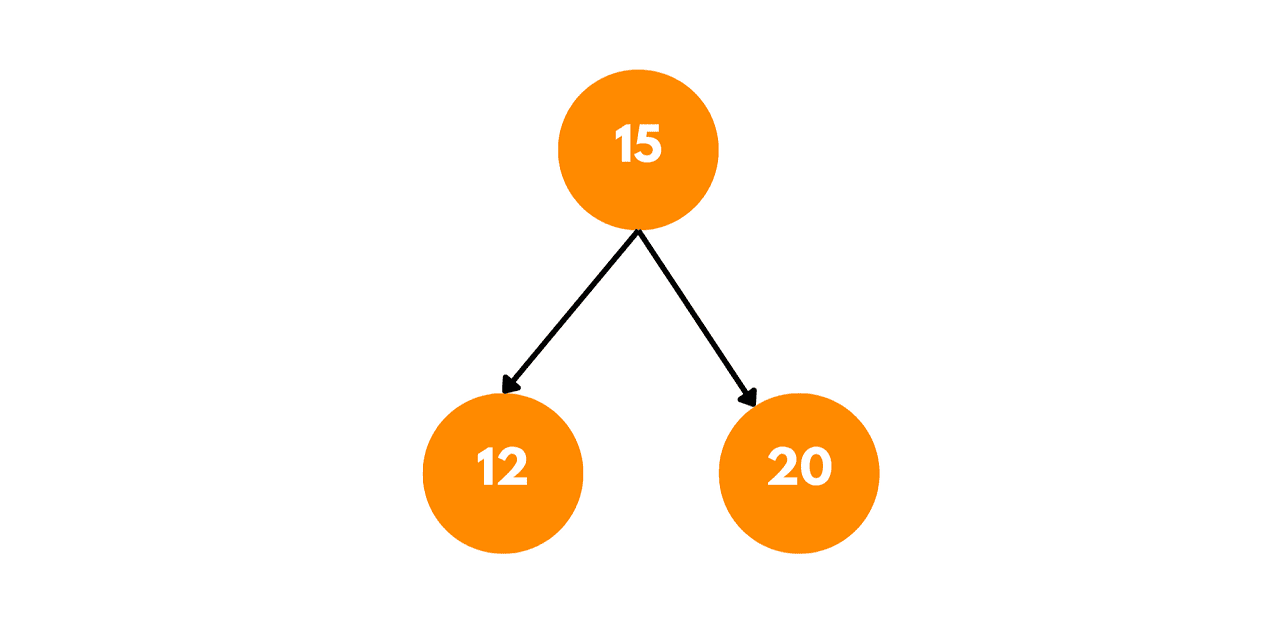
This subtree has a size of 3 and contains the nodes 12, 15, and 20, satisfying the properties of a BST.

The illustrated example demonstrates the process of finding the largest BST within a binary tree. By comparing the values of each subtree with the minimum and maximum values, we determine the validity of the subtree as a BST. The largest BST identified in the binary tree can provide valuable insights into its structure and hierarchical relationships.

Find the Largest BST in the Binary Tree

To find the largest Binary Search Tree (BST) in a binary tree, we will use Depth-First Traversal. Starting from the root of the binary tree, we perform a recursive traversal of both the left and right subtrees.

At each node, we compare its value with the minimum and maximum values of its left and right subtrees, ensuring that it satisfies the BST property. If a node violates the BST property, we discard the entire subtree rooted at that node and move to the next node.

Here's a step-by-step algorithm for finding the largest Binary Search Tree (BST) in a binary tree:

1. Define a class or structure to represent a BST node, containing the following attributes:

   • Value: the value of the node.
   • Left: a reference to the left child node.
   • Right: a reference to the right child node.

2. Define a class or structure to store the information about the largest BST found, containing the following attributes:

   • Size: the number of nodes in the BST.
   • MinValue: the minimum value in the BST.
   • MaxValue: the maximum value in the BST.
   • Root: a reference to the root node of the BST.

3. Create a function called largestBST that takes a binary tree's root node as input and returns the information about the largest BST found.

4. Inside the largestBST function, implement a recursive helper function called findLargestBST with the following parameters:

   • node: the current node being processed.
   • minValue: the minimum value that the subtree rooted at node can have.
   • maxValue: the maximum value that the subtree rooted at node can have.

5. If node is null, return information about an empty BST (size = 0, minValue = +∞, maxValue = -∞, root = null).

6. Recursively call findLargestBST for the left and right child nodes of node.

7. Compare the values returned by the left and right subtrees to determine the size, minValue, maxValue, and root of the BST rooted at node. There are three cases to consider: a. If both left and right subtrees are BSTs and the value of node is greater than the maximum value of the left subtree and less than the minimum value of the right subtree, then the subtree rooted at node is a BST. b. If either the left or right subtree is not a BST, or the value of node is not within the valid range, then the subtree rooted at node is not a BST. c. If the subtree rooted at node is a BST, update the information about the largest BST found so far if its size is greater than the current largest BST.

8. Return the information about the largest BST found among the left and right subtrees of node.

9. Finally, call the largestBST function with the root of the binary tree as the input, and retrieve the information about the largest BST found.

This algorithm employs a recursive approach to traverse the binary tree and evaluate each subtree, identifying the largest BST based on the properties of a BST.

C++ Implementation

Let's take a look at the implementation of the code for finding the largest BST in a binary tree in C++:

#include <iostream>
#include <climits>

// Structure for a BST node
struct Node {
    int data;
    Node* left;
    Node* right;
};

// Structure to store information about a BST
struct BSTInfo {
    int size;
    int minValue;
    int maxValue;
    Node* root;
};

// Helper function to create a new node
Node* createNode(int data) {
    Node* newNode = new Node();
    newNode->data = data;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Helper function to check if a binary tree is a BST
bool isBSTUtil(Node* node, int minValue, int maxValue) {
    if (node == nullptr)
        return true;

    if (node->data < minValue || node->data > maxValue)
        return false;

    return (isBSTUtil(node->left, minValue, node->data - 1) &&
            isBSTUtil(node->right, node->data + 1, maxValue));
}

// Main function to find the largest BST in a binary tree
BSTInfo largestBSTUtil(Node* node) {
    if (node == nullptr)
        return {0, INT_MAX, INT_MIN, nullptr};

    // Check if the current subtree is a BST
    if (isBSTUtil(node, INT_MIN, INT_MAX))
        return {1, node->data, node->data, node};

    // Recursively find the largest BST in the left and right subtrees
    BSTInfo leftBST = largestBSTUtil(node->left);
    BSTInfo rightBST = largestBSTUtil(node->right);

    // Determine the largest BST among the left and right subtrees
    if (leftBST.size > rightBST.size)
        return leftBST;
    else
        return rightBST;
}

// Wrapper function to find the largest BST in a binary tree
BSTInfo largestBST(Node* root) {
    return largestBSTUtil(root);
}

// Test the code with an example binary tree
int main() {
    Node* root = createNode(50);
    root->left = createNode(30);
    root->right = createNode(60);
    root->left->left = createNode(5);
    root->left->right = createNode(20);
    root->right->left = createNode(45);
    root->right->right = createNode(70);
    root->right->right->left = createNode(65);
    root->right->right->right = createNode(80);

    BSTInfo largestBSTInfo = largestBST(root);

    std::cout << "Size of the largest BST: " << largestBSTInfo.size << std::endl;

    // Printing the values of the largest BST
    std::cout << "Largest BST values: ";
    if (largestBSTInfo.root != nullptr) {
        std::cout << largestBSTInfo.root->data << " ";
        std::cout << largestBSTInfo.root->left->data << " ";
        std::cout << largestBSTInfo.root->right->data << " ";
    }
    std::cout << std::endl;

    return 0;
}

Output:

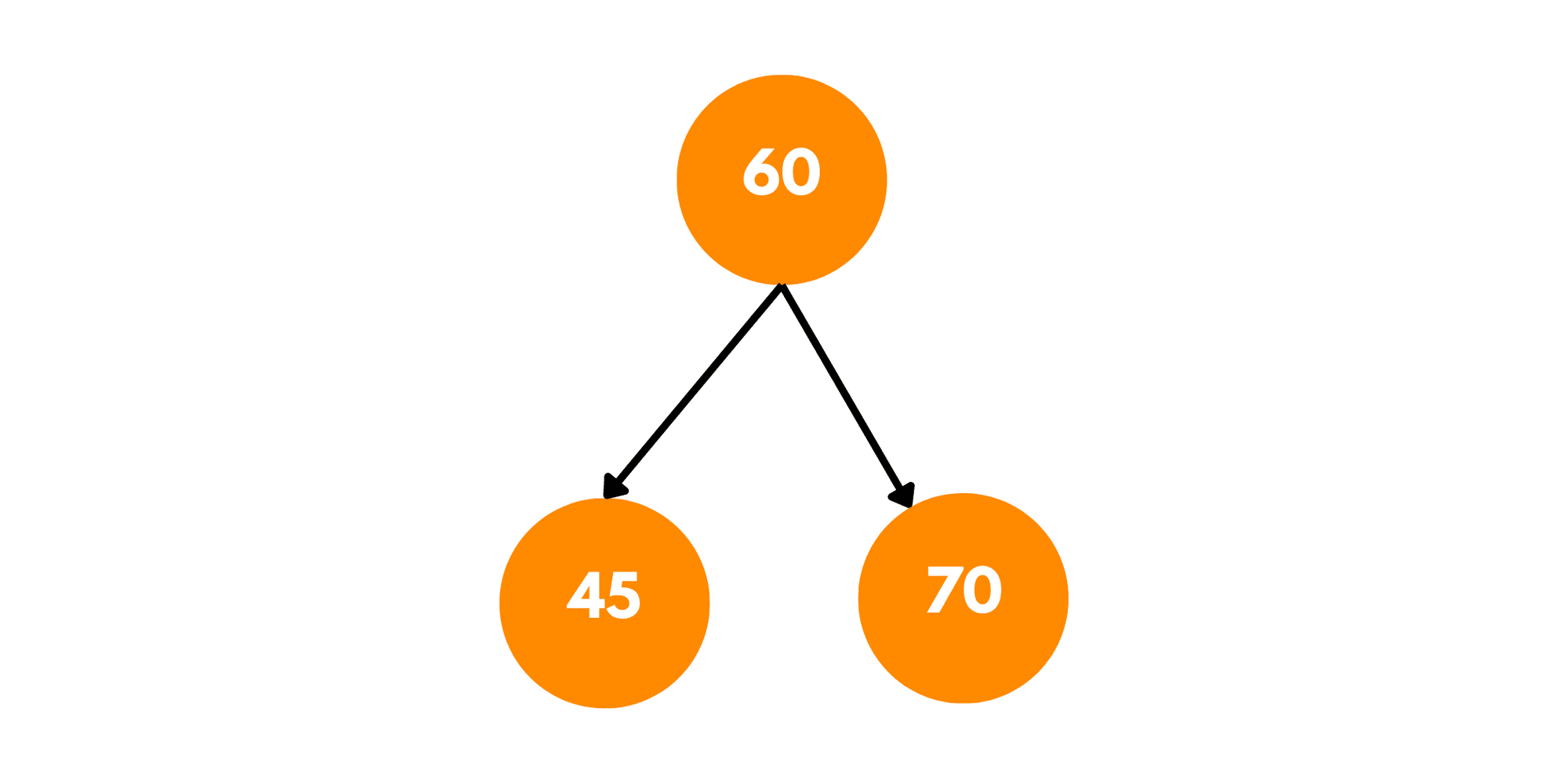
Size of the largest BST: 1
Largest BST values: 60 45 70 

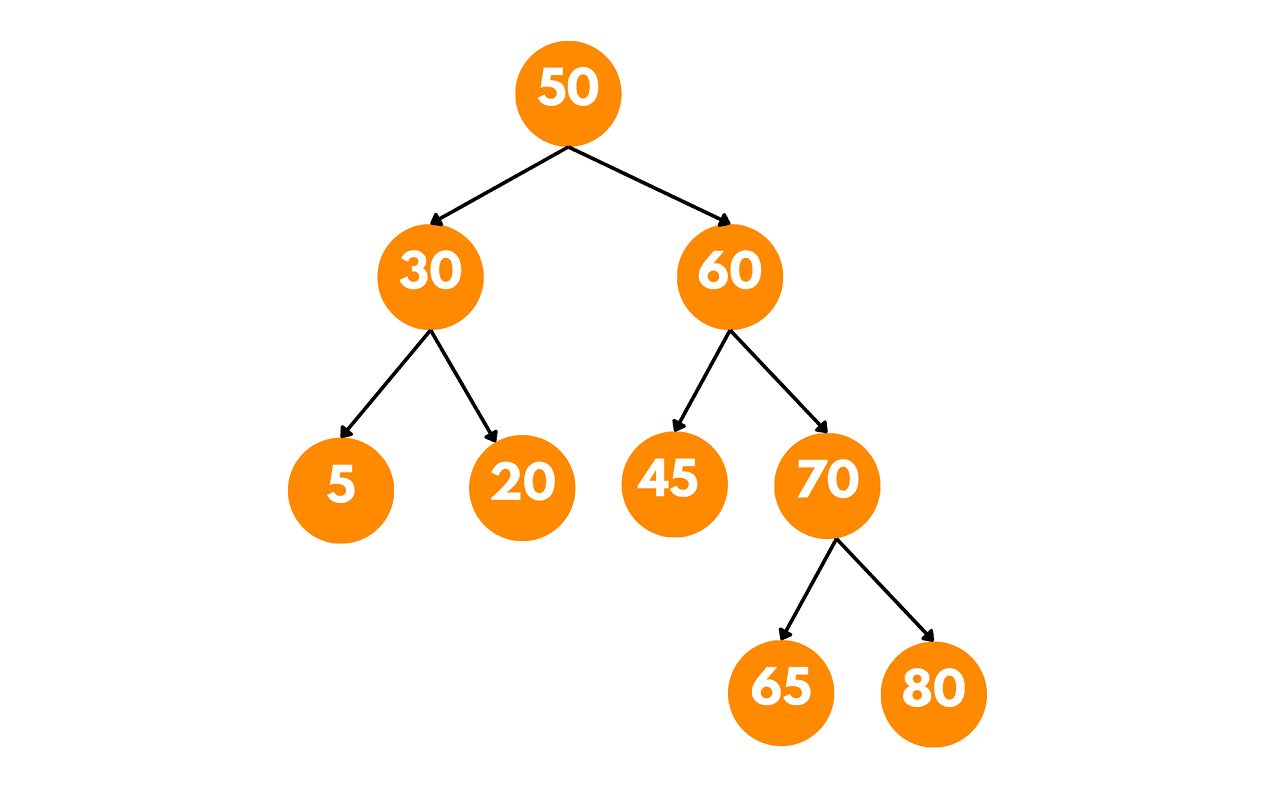
The tree we constructed is:

The largest subtree in a binary tree:

This code defines the necessary structures for a binary tree node and stores information about the largest BST found. It includes helper functions to create a new node and check if a binary tree is a BST. The main function largestBST is a wrapper that calls the largestBSTUtil function recursively to find the largest BST in the given binary tree.

Time and space Complexity

The time complexity of the code is O(n), where n is the number of nodes in the binary tree. This is because the code performs a depth-first traversal of the binary tree, visiting each node exactly once. The 'isBSTUtil' function also has a time complexity of O(n) since it checks if the subtree rooted at a node is a BST by traversing the subtree once.

The space complexity of the code is O(h), where h is the height of the binary tree. 

Conclusion

You now have the code to find the largest BST in the binary tree with its time and space complexities. Learn more about BST with examples here.