Finding the total number of islands is one of the most asked interview questions till date. A product-based company like Adobe and Infosys frequently asked this question as a part of their technical interview. As the number of island problems includes the concept and application of data structures and graphs, it helps the interviewer test the candidate's understanding for the same.
Problem: Find the Number of Islands
You are given a matrix “mat” with dimensions m*n, which represents a map of “1’s” as a land of the island and “0’s” as the water around the island. Island is surrounded by the water and connects adjacent lands horizontally and vertically, as shown in the figure below. Find out the total number of islands.
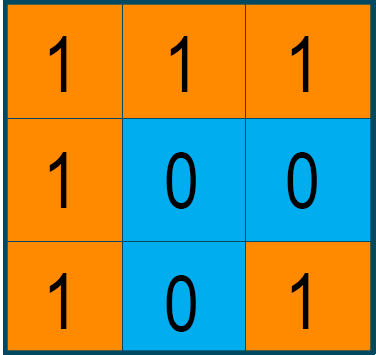
Before we start coding the problem's solution, let us first understand the problem description and working of the problem to find the solution.
Approach:
Looking at the above problem description, the "Number of island" problem is a variable of the standard problem “Find the number of connected components in an undirected graph.” As you know, a graph is a group of nodes and edges that are used to connect these nodes. Therefore, the connected component of an undirected graph is a subgraph where every two nodes are connected by a path(s). The below image shows the connected components of the graph.
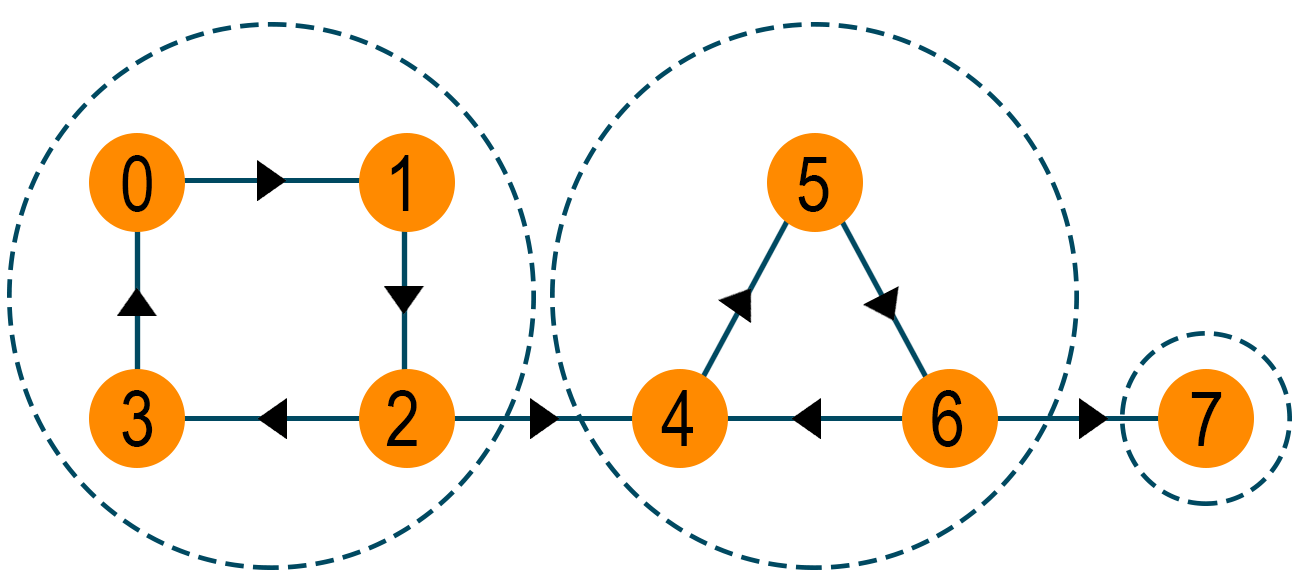
The given problem can be solved easily using Depth First Search Algorithm(DFS) on each component. Depth First Search Algorithm is a recursive algorithm that uses backtracking to search all the nodes of the graph by going ahead if the potential node is found, else use the backtracking approach. When DFS is called, a component of the undirect graph is visited. After the complete iteration, we will call DFS again on the next un-visited component. Therefore, the number of calls of DFS gives the total number of connected components of the graph.
Now comparing the connected components of an undirected graph with the "Number of island" problem, the node of the graph will be the “1’s” (land) in the matrix. We will call the depth-first search algorithm on the ‘1's’ of the matrix. Later during the DFS call, every visited cell of the matrix is set as ‘0’ to mark it as a visited node. At last, count the number of total DFS calls, which indicates the total number of islands since each DFS call starts when a new island is identified.
Let's take a look at the example below for a better understanding.
Example
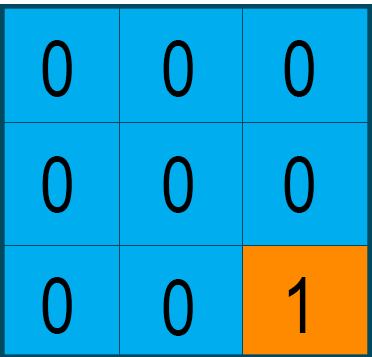
Consider a matrix “mat” of size 3x3 i.e. m=n=3. The “1’s” in the matrix represent the island's land area, and the “0’s” represent the water around the island.
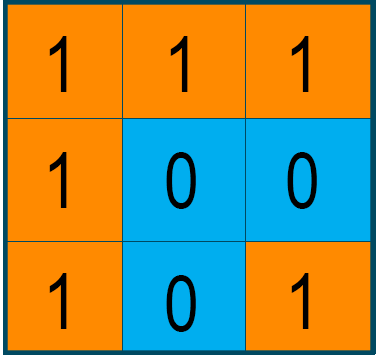
Now, we will call the DFS algorithm from the first cell, i.e., mat[0][0] of the matrix. The algorithm will traverse all the matrix cells containing “1’s” by using the recursive backtracking method, as shown below in the highlighted area.
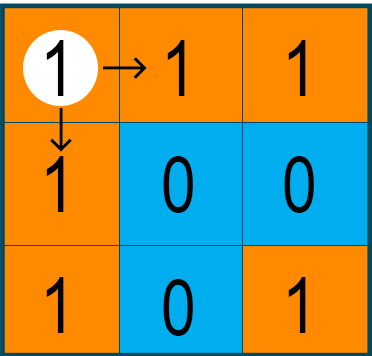
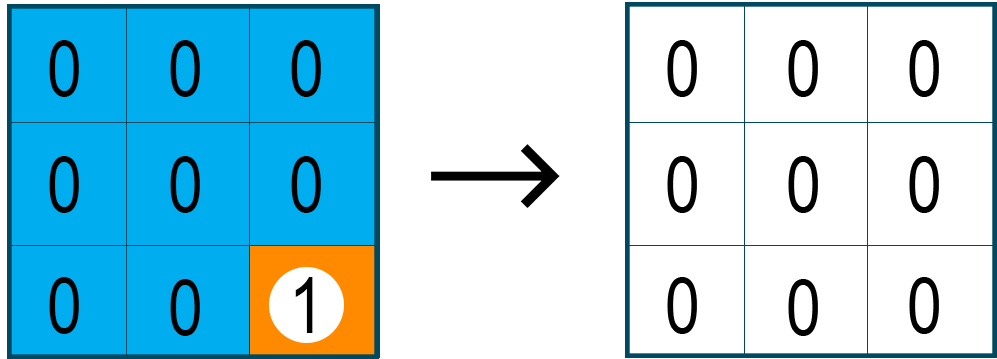
After each visit of the cell containing “1’s”, we will replace it with “0” to mark the cell as visited and avoid the repetition of the algorithm.
Later again, we call the DFS algorithm on the other matrix cell containing “1” but not visited previously. The process keeps repeating until all the cells of the matrix are zero.
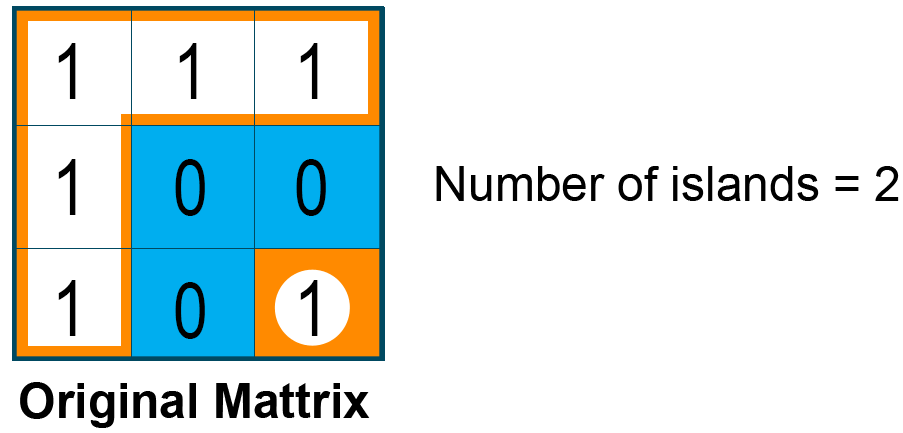
To find out the total number of islands as the final output of the problem, we will count the number of DFS calls throughout the problem. Therefore, for the given matrix, the number of islands is 2.
Time Complexity
The running time complexity for finding the number of islands for the given matrix is O(m*n), where m and n are rows and columns, respectively.
The space complexity of the problem is O(min(m,n)) as in the worst case where the matrix is filled with lands, and the size of the queue can grow up to min(m,n).
It's now time to test your own code in our compiler
Top 10 Problems
Number of Islands Solutions
1) C++ Code
#include<bits/stdc++.h> using namespace std; void DepthFirstSearch(vector<vector<int>> &mat, int i, int j, int row, int col) { if (i < 0 || j < 0 || i > (row - 1) || j > (col - 1) || mat[i][j] != 1){ // If index is not in range within range then return return; } if (mat[i][j] == 1){ mat[i][j] = 0; DepthFirstSearch(mat, i + 1, j, row, col); DepthFirstSearch(mat, i - 1, j, row, col); DepthFirstSearch(mat, i, j + 1, row, col); DepthFirstSearch(mat, i, j - 1, row, col); } } int NumIslands(vector<vector<int>> &mat, int row, int col){ int count = 0; for (int i = 0; i < row; i++){ for (int j = 0; j < col; j++){ if (mat[i][j] == 1){ mat[i][j] = 0; count++; DepthFirstSearch(mat, i + 1, j, row, col); DepthFirstSearch(mat, i - 1, j, row, col); DepthFirstSearch(mat, i, j + 1, row, col); DepthFirstSearch(mat, i, j - 1, row, col); } } } return count; } int main(){ int t; cin>>t; // t test cases while(t--){ int n,m,x; cin>>n>>m; vector<vector<int>> mat; // Input the mat for(int i=0;i<n;i++){ vector<int> p; for(int j=0;j<m;j++){ cin>>x; p.push_back(x); } mat.push_back(p); } cout<<NumIslands(mat,n,m)<<endl; } return 0; }
2) Java Code
/* package whatever; // don't place package name! */ import java.util.*; import java.lang.*; import java.io.*; /* Name of the class has to be "Main" only if the class is public. */ class Main { public static void main (String[] args) throws java.lang.Exception { Scanner sc = new Scanner(System.in); int testCases = sc.nextInt(); // Number of test cases for(int i=0;i<testCases;i++){ int m = sc.nextInt(); // Number of rows int n = sc.nextInt(); // Number of columns int mat[][] = new int[m][n]; for(int j=0;j<m;j++){ for(int k=0;k<n;k++){ mat[j][k] = sc.nextInt(); } } int numberOfIslands = 0; // Initializing number of islands with 0 for(int j=0;j<m;j++){ for(int k=0;k<n;k++){ if(mat[j][k] == 1){ countNumberOfIslands(j, k, mat); // recursive function which counts each island numberOfIslands+=1; } } } System.out.println(numberOfIslands); // Final result (Total number of islands) } } public static void countNumberOfIslands(int i, int j, int[][] mat){ if(i == mat.length || j == mat[0].length || i<0 || j<0) return; // base case if(mat[i][j] == 0) return; mat[i][j] = 0; countNumberOfIslands(i+1,j,mat); // checking in downward direction countNumberOfIslands(i,j+1,mat); // checking in right direction countNumberOfIslands(i-1,j,mat); // checking in upward direction countNumberOfIslands(i,j-1,mat); // checking in left direction } }
3) Python Code
class Solution : def Islands ( self , grid) : if not grid : return 0 def dfs ( i , j , grid ) : if i < 0 or j < 0 or i >= row or j >= col or grid [ i ] [ j ] == 0 : return grid [ i ] [ j ] = 0 # Mark cell as zero to avoid recounting dfs ( i + 1 , j , grid ) dfs ( i - 1 , j , grid ) dfs ( i , j + 1 , grid ) dfs ( i , j - 1 , grid ) return islands = 0 row = len ( grid ) col = len ( grid [ 0 ] ) for i in range ( 0 , row ) : # Traverse grid for j in range ( 0 , col ) : if grid [ i ] [ j ] == 1 : dfs ( i , j , grid ) islands += 1 return islands if __name__ == '__main__': mat = [[1, 1, 1], [1, 0, 0], [1, 0, 1 ]] print('Number of Islands : ',Solution().Islands(mat))


 Difficulty Level -
Difficulty Level -