Operators are the building block of any expression that we see. Be it mathematical or logical, without operators it would become very difficult to explain what operations we want to perform.
Imagine having to drive a car that does not have a steering wheel, it would be impossible to tell where the car is going to go. Similarly, without operators, we would not be able to make the compiler or interpreter of our code understand what operations we are performing. One such operator we shall see today is the XOR operator.
What is the XOR operator?
Also known as the exclusive OR, the XOR operator is a bitwise operator. What are bitwise operators? Any operator that operates on binary numbers is called a bitwise operator. They are used to perform some special operation on a binary string, that is a sequence of 0s and 1s.
Binary operators are used to performing operations on the bit level, which affects every bit in the number individually.
So, What is an exclusive OR operator? The XOR operation returns a 1 if the two operand bits are different and it returns 0 if the two operand bits are the same.
Let us simplify the technical jargon a bit! Take two binary numbers, 1100 and 0010. '⊕' is the symbol for the exclusive OR operation and the XOR operation between the two binary numbers can be written as:
1100 ⊕ 0010
the result of this will be 1110.
How did we get that result? Let us see the results bit by bit, literally speaking, have a look at the following table to understand how the results came.
| A | B | Result |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
What do we notice? When the two bits are different, the resulting bit is always 1 and when the two bits are the same, the resulting bit is always 0. That is the rule for Exclusive OR. Here is an image for easy reference:
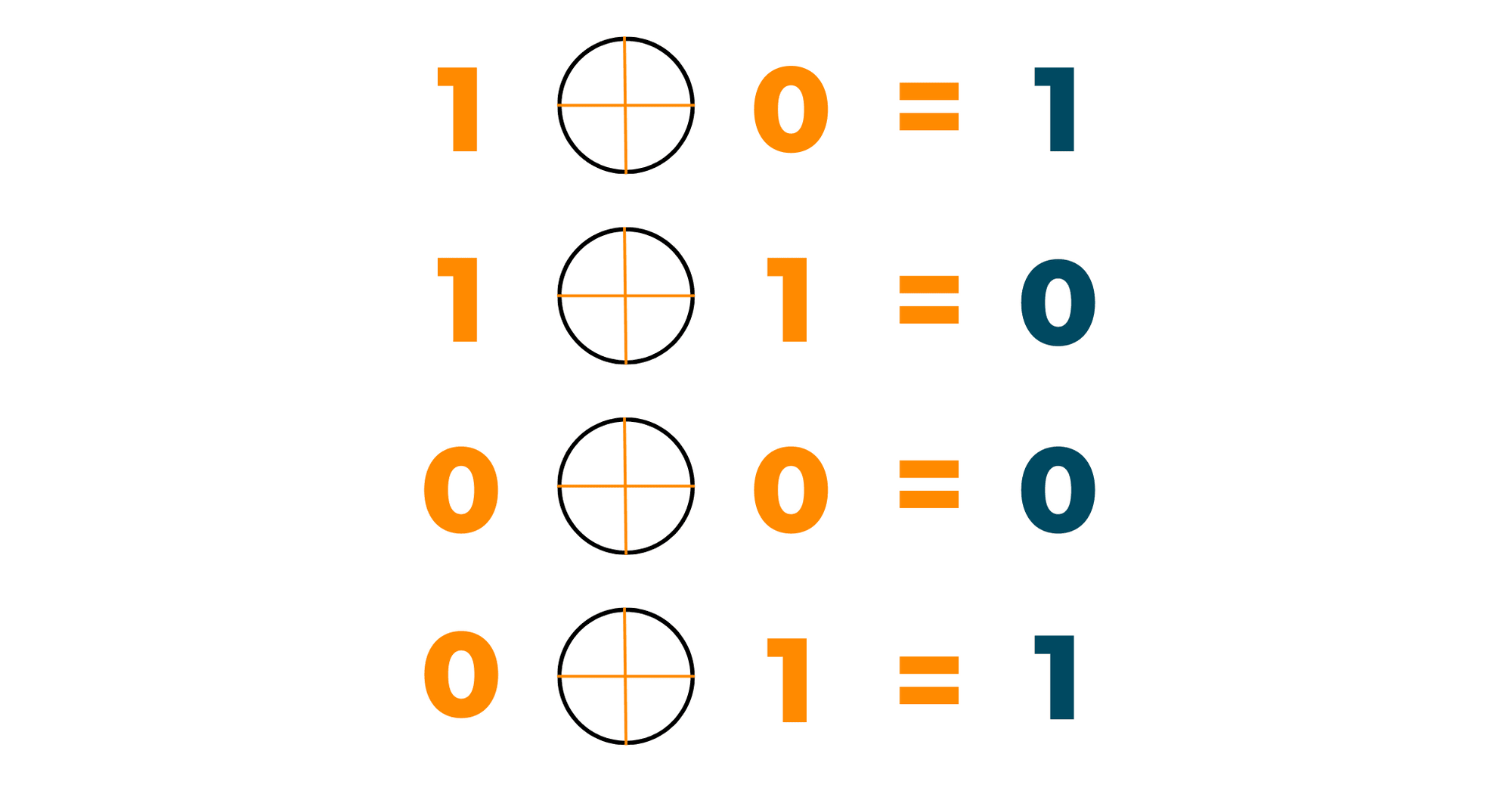
Now that we know how it works mathematically, let's see its implementation in python.
How to find XOR value in python?
The XOR operator in python can be applied using the “^” symbol. The XOR operator is used in various situations that we shall see in the section below, for now, let us have a look at how the code is implemented:
A = 0b1100 B = 0b0010 print(bin(A^B))
Output:
0b1110
Use cases of XOR
01) Encryption
Exclusive OR is one of the first methods that was used in encryption. It is a very naive method but it is very easy to implement. Though using exclusive OR alone is a very weak method of implementing encryption, combined with other methods, it can create powerful encryption.
Let us have a look at an example of how encryption using XOR or exclusive OR would look. We have a data item '10' that we want to send across to our friend. First, we decide on a key, which is a number that only we and our friends will know. Let us say this key is 5. The next step is using this key for encrypting the number.
We perform the XOR operation on 10 and 5. The interpreter will first convert the decimal numbers to binary numbers and then perform the operation. Once the resulting binary number is found, it converts it back to a decimal number again. So,
10 ⊕ 5 = 1010 ⊕ 0101 = 1111 = 15
After getting the result 15 we send the encrypted message to our friend. Our friend receives the encrypted message 15 and needs to extract the actual message. They use the common key we had decided first, they perform the XOR operation on 15 and 5.
15 ⊕ 5 = 1111 ⊕ 0101 = 1010 = 10
Now our friend has the original message.
02) Swapping Two Numbers
We just saw how the XOR operation is used for encryption, let us now see how it can be used to perform the swap between two numbers. Let us say we have two numbers 10 and 15 that we wish to swap. 10 is stored in variable A and 15 is stored in variable B. We perform the swaps using the XOR operation in the following manner:
A ⊕ B = 10 ⊕ 15 = 1010 ⊕ 1111 = 0101 = 5
We store the result in A, so A becomes 0101. Now, we do A ⊕ B again,
A ⊕ B = 5 ⊕ 15 = 0101 ⊕ 1111 = 1010 = 10
We store this result in B, so B becomes 1010. Then we perform A ⊕ B again,
A ⊕ B = 0101 ⊕ 1010 = 1111 = 15
We store this result in A. Therefore now the values of A and B are 15 and 10. The swap has taken place. What actions did we perform?
- A = A ⊕ B
- B = A ⊕ B
- A = A ⊕ B
Here is the source code for implementation:
A = 10 B = 15 print("Before:",A,B) A = A^B B = A^B A = A^B print("After",A,B)
Output:
Before: 10 15 After 15 10
03) Checking equality
How do we use XOR for checking equality? Do we know the fundamental rule about XOR? It returns 1 if the two operands are different and 0 if the two operands are the same.
Let us say we had to compare two boolean values. We can XOR the two boolean values and if it returns 1 we can say they are not equal and if it returns 0 we can say they are equal.
Conclusion
We saw one of the bitwise operators, the XOR or Exclusive OR operator. Bitwise operators work on the given operands one bit by one bit. The XOR operation is also used for various tasks like encryption, swapping, and equality checks.








