The hiring process of various companies has evolved over the years. They have extended their part to making the candidates solve tough puzzles using their code implementation. But why? Well, for starters the analytical skills can be tested, and secondly, the coding skills are used to get the most optimal way to solve the riddle. In today's article, we are going to understand and solve a well-known problem called the Water Jug Problem. We will understand the problem, check an example, and methods to solve it in three different languages: C++, Java, and Python.
What is the Water Jug Problem?
Here is the problem statement for Water Jug Problem:
You are given 2 jugs with the capacity 'm' and 'n' respectively. Initially, they are given empty. There is an unlimited supply of water. You can either fill the whole jug or a quantity that is less than the given capacity of jugs. Now, you are also given a third positive integer 'd'. Using the 2 given jugs, you need to come up with a solution to have 'd' amount of water in them and return the number of steps you took to reach that capacity.
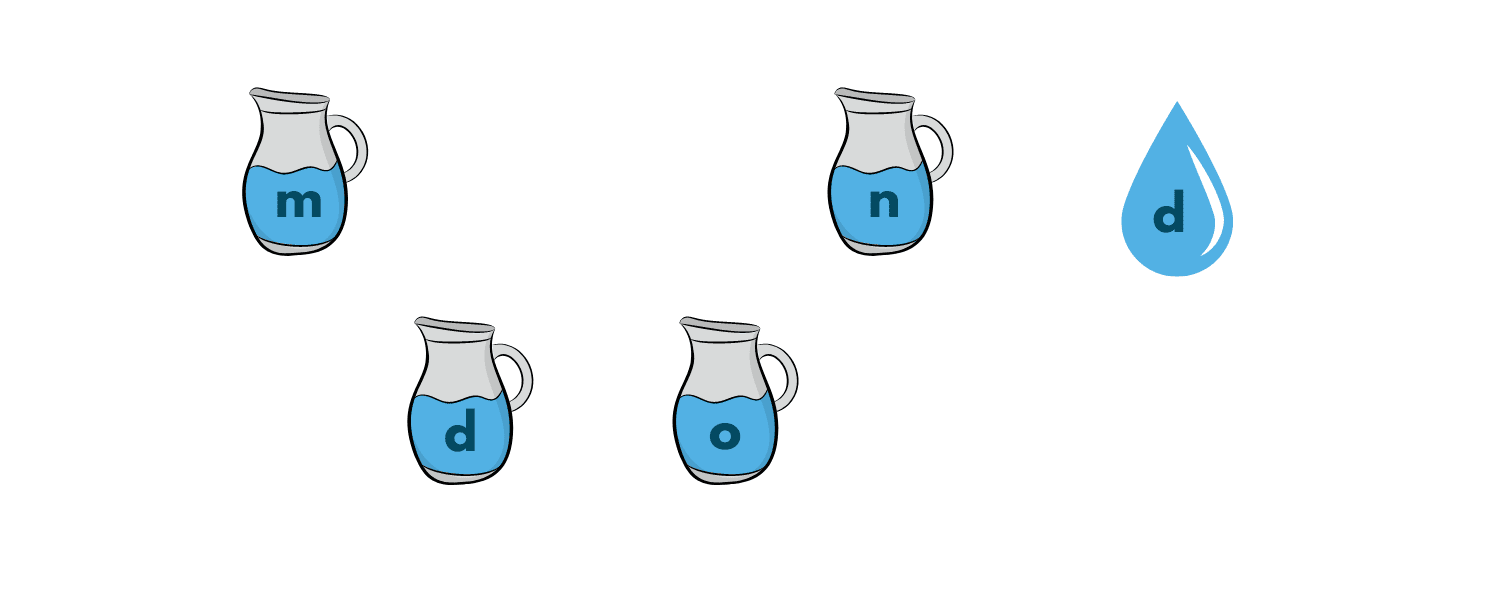
Understanding the Problem
Before beginning the coding part, it is very important for you to understand what the question is asking you to do. Many students just copy the code from web servers and later, when the interviewer asks any question from it, they are stuck and even embarrassed. So, to save yourself from such questions, kindly go through this section carefully.
So, you are given 2 jugs with their capacities. It has also been clearly stated in the question that with the unlimited water supply, you can either fill the whole jug up to its capacity or somewhat less than that. Keep that in mind.
Secondly, we need to find a way to somehow have a 'd' amount of water left in the jugs. Basically, we need to transfer, fill and, empty the jugs to get the required capacity of water in the jugs.
The next most important question is which data structure should you choose for this question. You cannot use arrays as it will be a heavy task for both the compiler(in terms of time and auxiliary space complexity) and you(in terms of long codes).
You should choose a structure with which you can manage the content of both jugs simultaneously on the front. The possible and safest option is to use Sets or Pairs.
How to Approach the Solution?
Now that we have chosen what to work with, let's understand how you can actually make it work. Well, for starters you can have (a, b) which represents the amount of water currently in jug 1 and jug 2 respectively. Initially, both the components will be (0, 0) since the jugs are empty in the beginning. The final state of the jugs will be either (0, d) or (d, 0) as both add up to give a total of the required quantity.
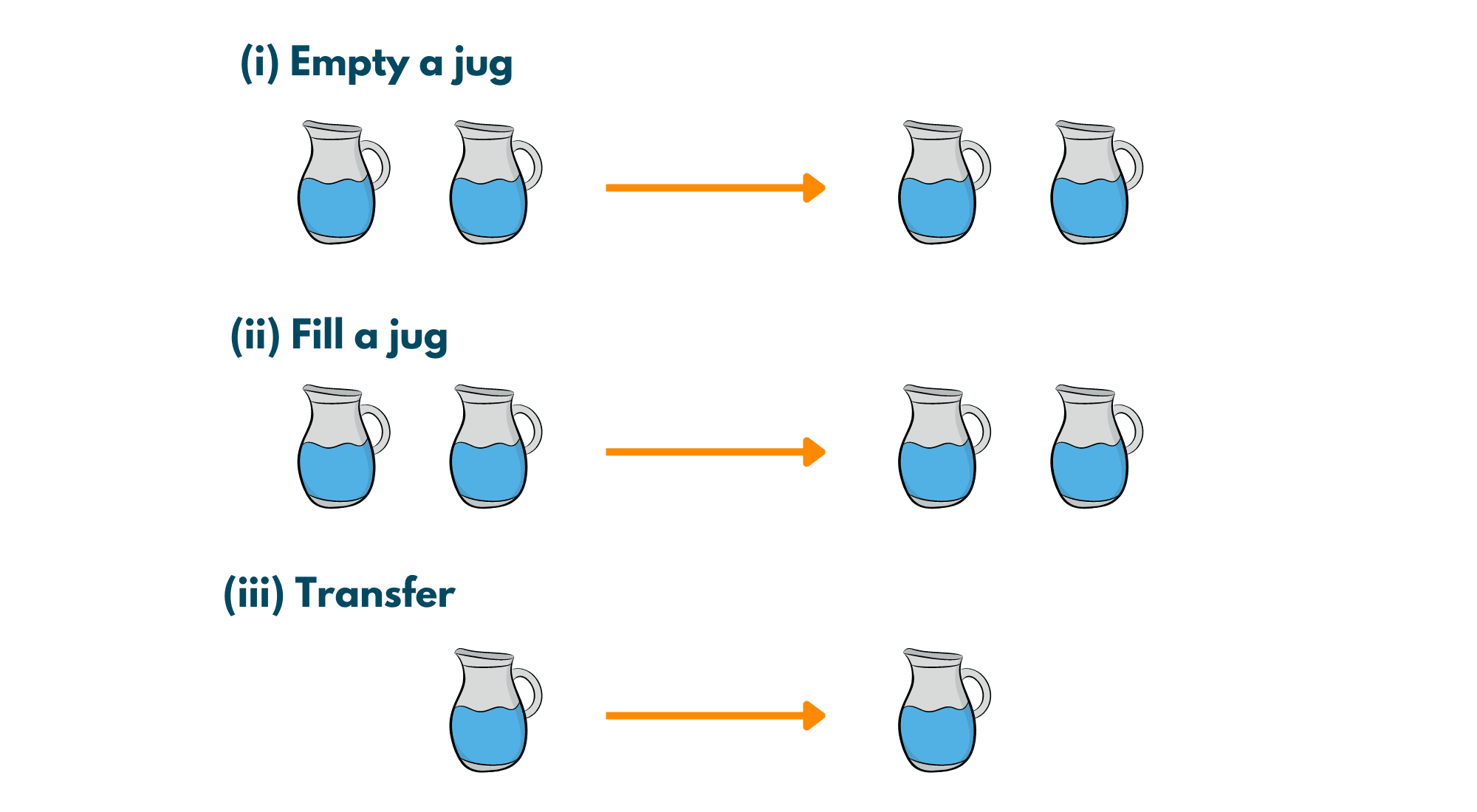
The following operations can be performed on the jugs:
- Empty a jug (a, b) -> (0, b)
- Fill a jug (0, b) -> (a, b)
- Transfer water from one jug to another.
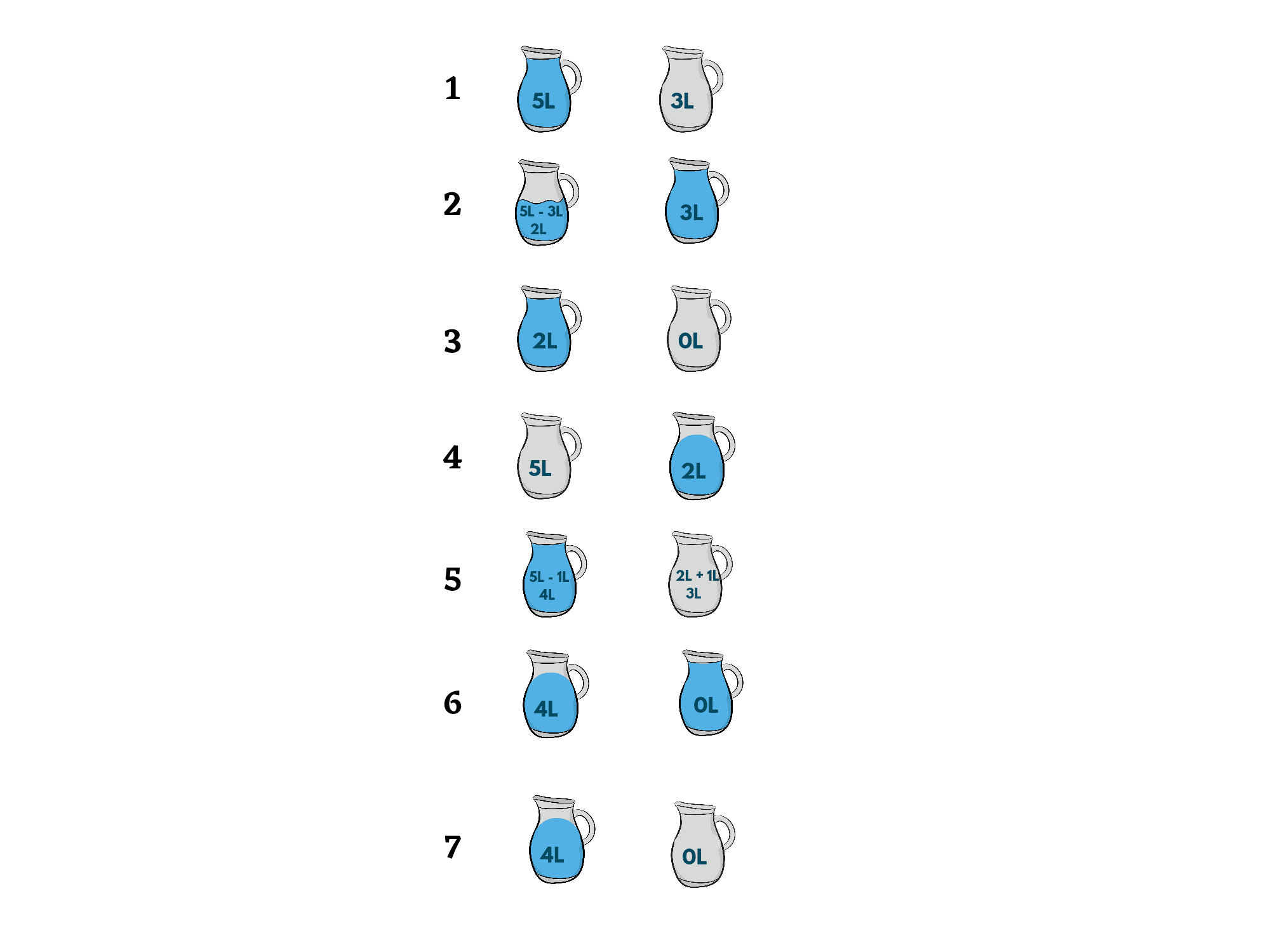
Example
Input: 3, 5, 4
Output: 6
Explanation: The following steps are taken:
- Fill the 5-liter jug completely.
- Transfer 3 liters from a 5-liter jug to a 3-liter jug.
- Empty the 3-liter capacity jug.
- Transfer the remaining 2 liters from a 5-liter jug to a 3-liter jug.
- Now, fill the 5-liter jug fully.
- Pour 1 liter from a 5-liter jug into a 3-liter jug.
- There! We have 4 liters in the first jug, now empty the 2nd jug.
For more clarity, check the below illustration.
3 Methods to Solve the Water Jug Problem
Now, you know what the problem is and what is the approach behind the solution. Next, discuss some methods with which you can code this problem. Following are the three methods, you can use:
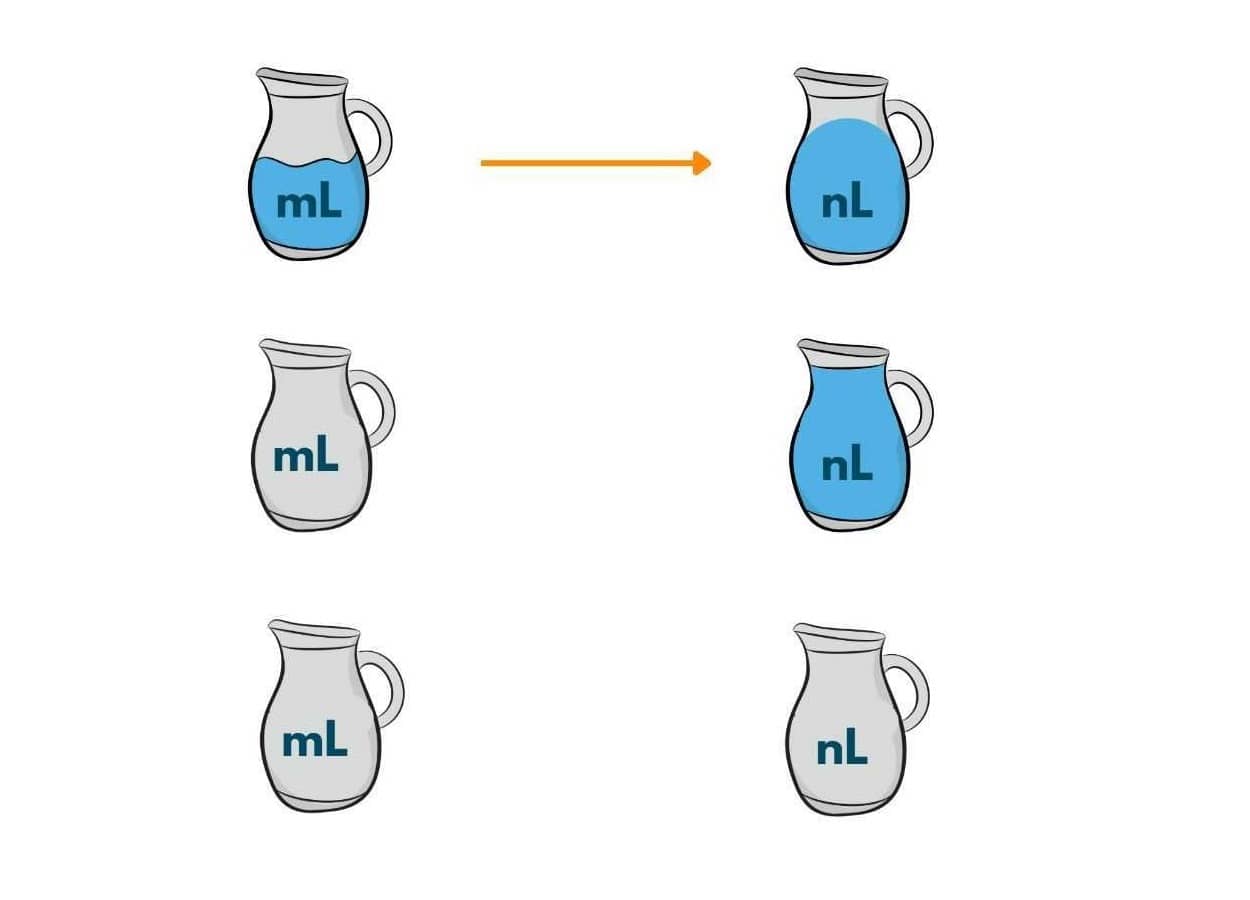
Method 01) Always pour from 1st jug to 2nd jug
- Fill the m liter jug and empty it into the n liter jug.
- When the m liter jug becomes empty refill it.
- When the n-liter jug becomes full, empty it.
- Repeat the above steps till any one of the jugs contains the required amount of water in them.
Method 02) Always pour from 2nd jug to 1st jug
- Fill the n-liter jug and empty it into the m-liter jug.
- When the n liter jug becomes empty refill it.
- When the m liter jug becomes full, empty it.
- Repeat the above steps till any of the jugs contain the required amount of water in them.
Method 03) Using BFS(Breadth First Search)
In the BFS method, we use a queue and a map to find the solution. In the beginning, we initialize it with zero as both the jugs are empty. We then keep applying the above operations that are permitted to us and find the possible scenarios to find the targeted amount of water in the jugs.
Also, we keep maintaining an empty matrix to keep a track of the positions or states that we have encountered. In this way, the space complexity reduces manifolds and the efficiency of the program continuously improves.
Code Implementation with C++
Here is the C++ code to solve the Water Jug Problem:
#include <bits/stdc++.h> using namespace std; typedef pair<int, int> p; void printPath(map<p, p> mp, p u) { if (u.first == 0 && u.second == 0) { cout << 0 << " " << 0 << endl; return; } printPath(mp, mp[u]); cout << u.first << " " << u.second << endl; } void BFSSolution(int x, int y, int target) { map<p, int> m; bool isSolvable = false; map<p, p> mp; queue<p> q; q.push(make_pair(0, 0)); while (!q.empty()) { auto u = q.front(); q.pop(); if (m[u] == 1) continue; if ((u.first > x || u.second > y || u.first < 0 || u.second < 0)) continue; m[{u.first, u.second}] = 1; if (u.first == target || u.second == target) { isSolvable = true; printPath(mp, u); if (u.first == target) { if (u.second != 0) cout << u.first << " " << 0 << endl; } else { if (u.first != 0) cout << 0 << " " << u.second << endl; } return; } // Filling the 2nd jug completely if (m[{u.first, y}] != 1) { q.push({u.first, y}); mp[{u.first, y}] = u; } // Filling the 1st jug completely if (m[{x, u.second}] != 1) { q.push({x, u.second}); mp[{x, u.second}] = u; } // Transferring contents of 1st Jug to 2nd Jug int d = y - u.second; if (u.first >= d) { int c = u.first - d; if (m[{c, y}] != 1) { q.push({c, y}); mp[{c, y}] = u; } } else { int c = u.first + u.second; if (m[{0, c}] != 1) { q.push({0, c}); mp[{0, c}] = u; } } // Transferring content of 2nd jug to 1st jug d = x - u.first; if (u.second >= d) { int c = u.second - d; if (m[{x, c}] != 1) { q.push({x, c}); mp[{x, c}] = u; } } else { int c = u.first + u.second; if (m[{c, 0}] != 1) { q.push({c, 0}); mp[{c, 0}] = u; } } // Emptying 2nd Jug if (m[{u.first, 0}] != 1) { q.push({u.first, 0}); mp[{u.first, 0}] = u; } // Emptying 1st jug if (m[{0, u.second}] != 1) { q.push({0, u.second}); mp[{0, u.second}] = u; } } if (!isSolvable) cout << "Solution not possible"; } int main() { int Jug1 = 4, Jug2 = 3, target = 2; cout << "Path from initial state " "to solution state ::\n"; BFSSolution(Jug1, Jug2, target); return 0; }
Code Implementation with Java
Here is the Java code to solve this problem:
import java.util.*; class Pair { int p1, p2; List<Pair> path; Pair(int p1, int p2) { this.p1 = p1; this.p2 = p2; path = new ArrayList<>(); } Pair(int p1, int p2, List<Pair> _path) { this.p1 = p1; this.p2 = p2; path = new ArrayList<>(); path.addAll(_path); path.add(new Pair(this.p1, this.p2)); } } public class Solution { public static void main(String[] args) throws java.lang.Exception { int Jug1 = 4; int Jug2 = 3; int target = 2; getPathIfPossible(Jug1, Jug2, target); } private static void getPathIfPossible(int Jug1, int Jug2, int target) { boolean[][] visited = new boolean[Jug1 + 1][Jug2 + 1]; Queue<Pair> queue = new LinkedList<>(); Pair initialState = new Pair(0, 0); initialState.path.add(new Pair(0, 0)); queue.offer(initialState); while (!queue.isEmpty()) { Pair curr = queue.poll(); if (curr.p1 > Jug1 || curr.p2 > Jug2 || visited[curr.p1][curr.p2]) continue; visited[curr.p1][curr.p2] = true; if (curr.p1 == target || curr.p2 == target) { if (curr.p1 == target) { curr.path.add(new Pair(curr.p1, 0)); } else { curr.path.add(new Pair(0, curr.p2)); } int n = curr.path.size(); System.out.println("Path of states of jugs followed is :"); for (int i = 0; i < n; i++) System.out.println(curr.path.get(i).p1 + " , " + curr.path.get(i).p2); return; } queue.offer(new Pair(Jug1, 0, curr.path)); queue.offer(new Pair(0, Jug2, curr.path)); queue.offer(new Pair(Jug1, curr.p2, curr.path)); queue.offer(new Pair(curr.p1, Jug2, curr.path)); queue.offer(new Pair(0, curr.p2, curr.path)); queue.offer(new Pair(curr.p1, 0, curr.path)); int emptyJug = Jug2 - curr.p2; int amountTransferred = Math.min(curr.p1, emptyJug); int p2 = curr.p2 + amountTransferred; int p1 = curr.p1 - amountTransferred; queue.offer(new Pair(p1, p2, curr.path)); emptyJug = Jug1 - curr.p1; amountTransferred = Math.min(curr.p2, emptyJug); p2 = curr.p2 - amountTransferred; p1 = curr.p1 + amountTransferred; queue.offer(new Pair(p1, p2, curr.path)); } System.out.println("Not Possible to obtain target"); } }
Code Implementation with Python
Here is the Python code to solve the Water Jug Problem:
from collections import deque def Solution(a, b, target): m = {} isSolvable = False path = [] q = deque() #Initializing with jugs being empty q.append((0, 0)) while (len(q) > 0): # Current state u = q.popleft() if ((u[0], u[1]) in m): continue if ((u[0] > a or u[1] > b or u[0] < 0 or u[1] < 0)): continue path.append([u[0], u[1]]) m[(u[0], u[1])] = 1 if (u[0] == target or u[1] == target): isSolvable = True if (u[0] == target): if (u[1] != 0): path.append([u[0], 0]) else: if (u[0] != 0): path.append([0, u[1]]) sz = len(path) for i in range(sz): print("(", path[i][0], ",", path[i][1], ")") break
q.append([u[0], b]) # Fill Jug2 q.append([a, u[1]]) # Fill Jug1 for ap in range(max(a, b) + 1): c = u[0] + ap d = u[1] - ap if (c == a or (d == 0 and d >= 0)): q.append([c, d]) c = u[0] - ap d = u[1] + ap if ((c == 0 and c >= 0) or d == b): q.append([c, d]) q.append([a, 0]) q.append([0, b]) if (not isSolvable): print("Solution not possible") if __name__ == '__main__': Jug1, Jug2, target = 4, 3, 2 print("Path from initial state " "to solution state ::") Solution(Jug1, Jug2, target)
Output:
Path of states by jugs followed is : 0 , 0 0 , 3 3 , 0 3 , 3 4 , 2 0 , 2
Complexity Analysis
Time Complexity for the solution will be O(n*m) and the Space Complexity for it will be O(n*m).
Conclusion
After reading this article, it is certain that you must have understood the Water Jug problem and the approaches with which it can be solved. By exploring different approaches and solutions, we can find efficient ways to measure out specific quantities of water using limited resources. Whether you choose to pour from the smaller jug into the larger one or vice versa, the key is to find the solution that minimizes the number of steps required.








