Topological Sort Python Code for Directed Acyclic Graph

In this article, we will study what is topological sort and how it works. We will understand the examples explaining the topological sort and the corresponding python code to get the sequence of an array following the topological sort algorithm. Lastly, we will study the time complexity of the algorithm and the applications of the topological sort. So, let’s get started!

What is Topological Sort?

Topological sort is an algorithm that takes a directed acyclic graph and returns the sequence of nodes where every node will appear before other nodes that it points to. Just to remind, a directed acyclic graph (DAG) is the graph having directed edges from one node to another but does not contain any directed cycle. Remember topological sorting for graphs is not applicable if the graph is not a Directed Acyclic Graph (DAG). The ordering of the nodes in the array is called topological ordering. Therefore we can say that a topological sort of the nodes of a directed acyclic graph is the operation of arranging the nodes in the order in such a way that if there exists an edge (i,j), i precedes j in the lists. A topological sort basically gives a sequence in which we should perform the job and helps us to check whether the graph consists of the cycle or not.

Every graph can have more than one topological sorting possible. It depends on the in-degree of the node in the graph. Also, the topological sorting of the graph starts with the node that has in-degree as 0 i.e a node with no incoming edges. Let us learn an example for a clear understanding. 

Example

Consider the following directed acyclic graph with their in-degree mentioned.

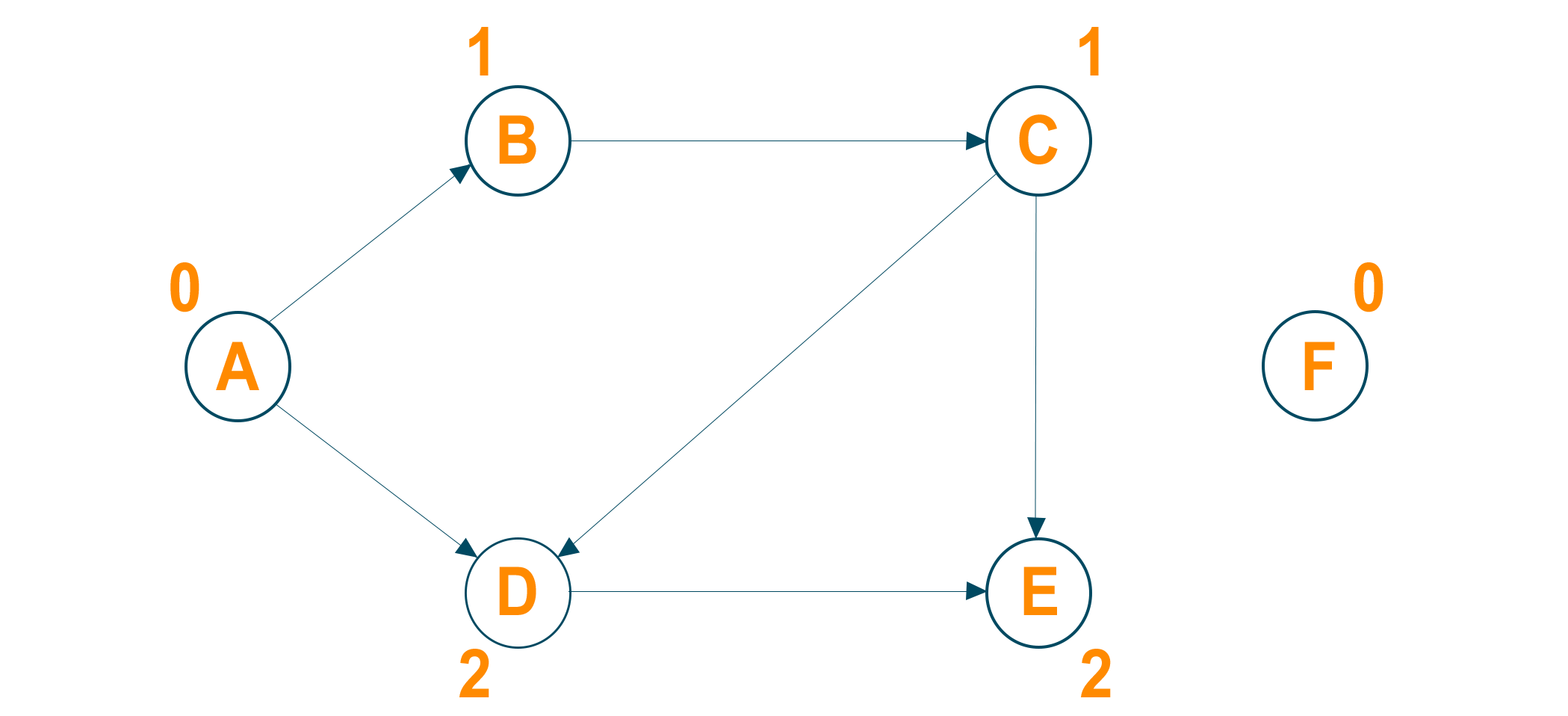
Identifying vertices that have no incoming edge. Here, nodes A and F have no incoming edges. 

We will choose node A as the source node and deletes this node with all its outgoing edges and put it in the result array. 

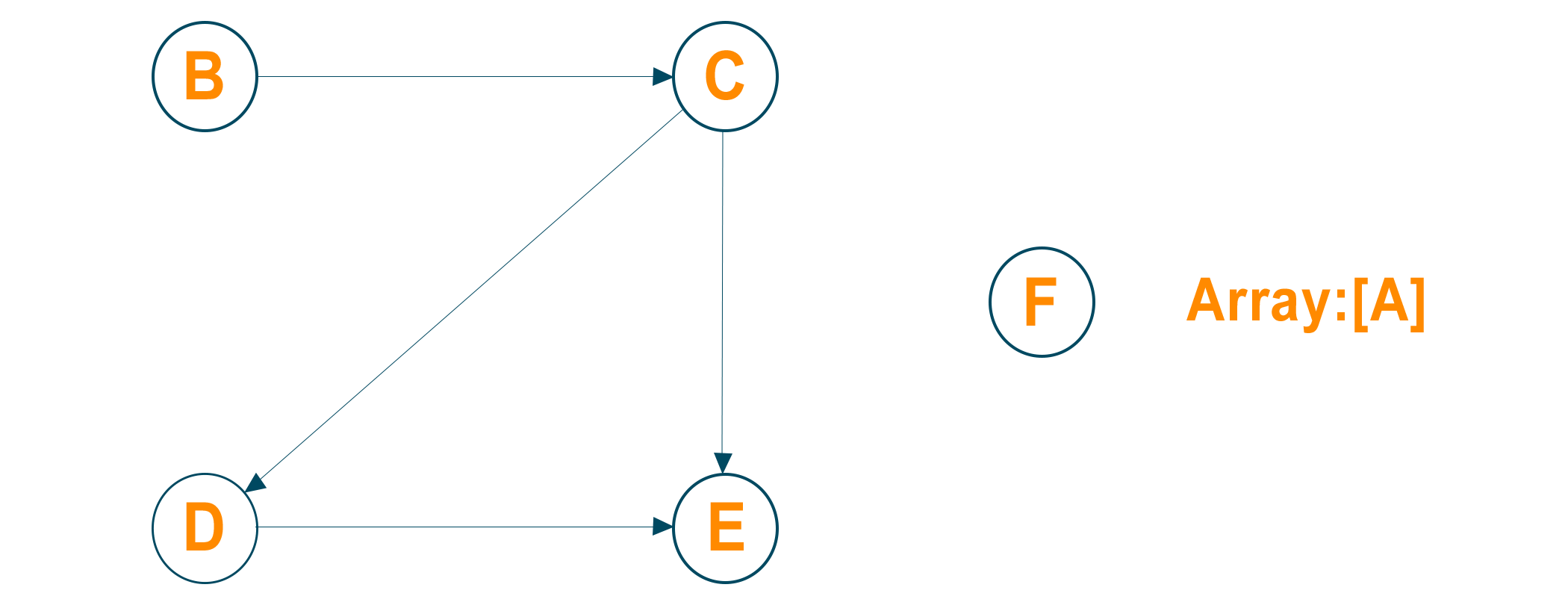
Now, update the in-degree of the adjacent nodes of the source node after deleting the outgoing edges of node A

Now again delete the node with in-degree 0 and its outgoing edges and insert it in the result array. Later update the in-degree of all its adjacent nodes. 

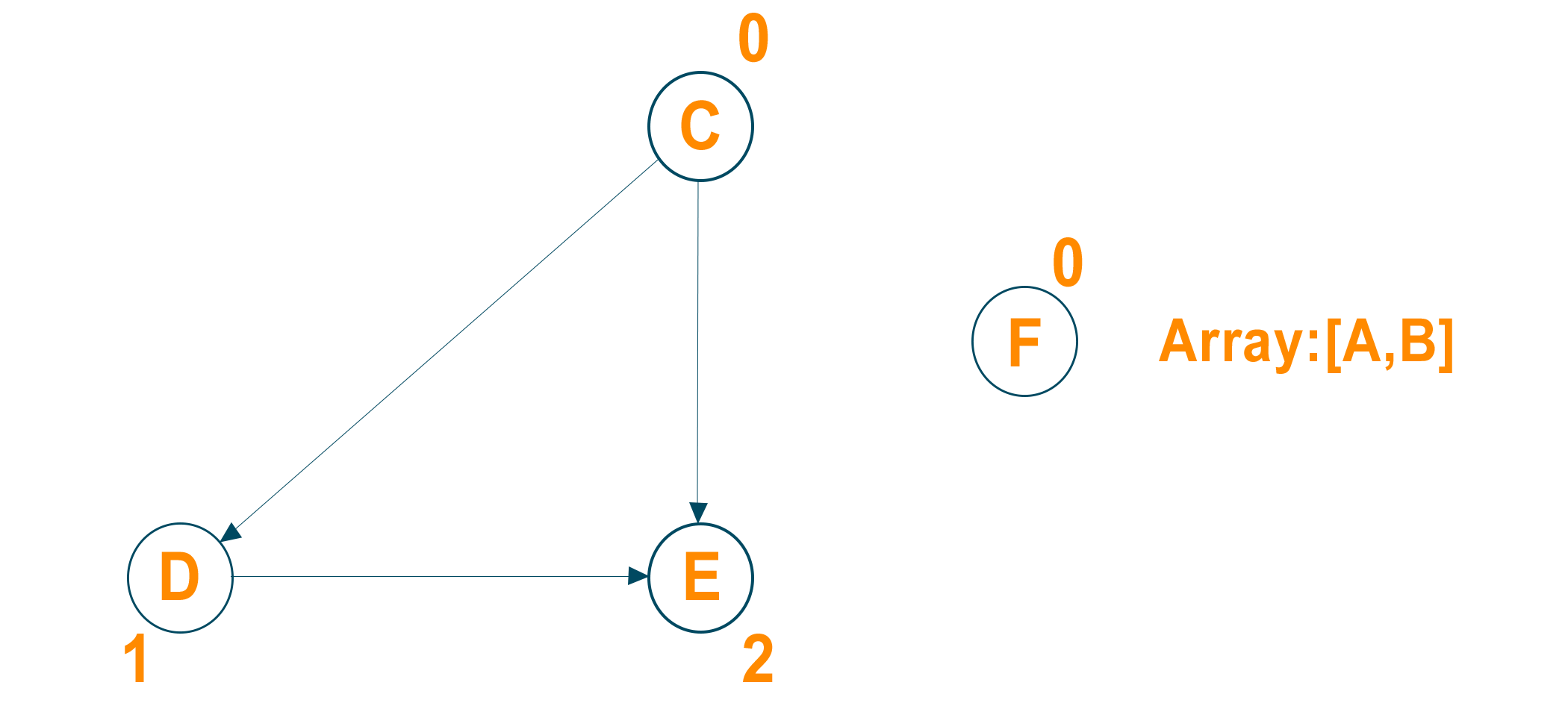
Now repeat the above steps to get output as below:

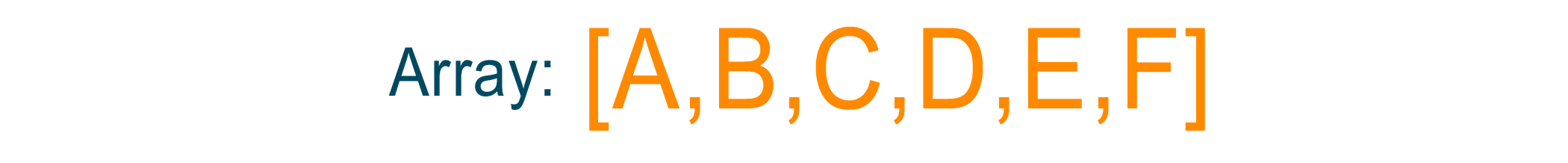
In the second step, if we have chosen the source node as F then the topological sort of the graph will be F, A, B, C, D, E. Therefore, there is more than one topological sort possible for every directed acyclic graph.  

Algorithm

The algorithm of the topological sort goes like this:

1. Identify the node that has no in-degree(no incoming edges) and select that node as the source node of the graph
2. Delete the source node with zero in-degree and also delete all its outgoing edges from the graph. Insert the deleted vertex in the result array.
3. Update the in-degree of the adjacent nodes after deleting the outgoing edges
4. Repeat step 1 to step 3 until the graph is empty

The resulting array at the end of the process is called the topological ordering of the directed acyclic graph. If due to some reason, there are some nodes left but they have the incoming edges, that means that the graph is not an acyclic graph and topological ordering does not exist.

Python Code For Topological Sort

from collections import defaultdict

class Graph:

    def __init__(self,n):

        self.graph = defaultdict(list)

        self.N = n

    def addEdge(self,m,n):

        self.graph[m].append(n)

    def sortUtil(self,n,visited,stack):

        visited[n] = True

        for element in self.graph[n]:

            if visited[element] == False:

                self.sortUtil(element,visited,stack)

        stack.insert(0,n)

    def topologicalSort(self):

        visited = [False]*self.N

        stack =[]

        for element in range(self.N):

            if visited[element] == False:

                self.sortUtil(element,visited,stack)

        print(stack)

graph = Graph(5)
graph.addEdge(0,1);
graph.addEdge(0,3);
graph.addEdge(1,2);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(3,4);

print("The Topological Sort Of The Graph Is:  ")

graph.topologicalSort()

Output

The Topological Sort Of The Graph Is:
[0, 1, 2, 3, 4]

Topological Sort Time Complexity

The running time complexity of the topological sorting algorithm is O(M + N) where the M is the number of edges in the graph and N is the number of nodes in the graph. We have to determine the in-degree of each node in the graph which takes total O(M) time and then runs the simple loop to place all the nodes in the result array by checking the in-degrees to be zero which takes total O(N) time for N number of nodes. Therefore the total time complexity of the program will be O(M+N). The space complexity for the algorithm will be O(N) where N is the total number of nodes in the graph to allocate the nodes in the result array.

Applications 

1. Topological sort can be used to quickly find the shortest paths from the weighted directed acyclic graph.
2. It is used to check whether there exists a cycle in the graph or not
3. Topological sort is useful to find the deadlock condition in an operating system
4. It is used in course scheduling problems to schedule jobs
5. It is used to find the dependency resolution
6. Topological sort is very useful to find sentence ordering in very fewer efforts
7. It is used in manufacturing workflows or data serialization in an application
8. It is used for ordering the cell evaluation while recomputing formula values in an excel sheet or spreadsheet.

Conclusion

It is easy to determine the order of the compilation tasks to perform using the topological algorithm. With many different applications in real life, topological sort has its own importance while exploring and working trees and graphs. Topological sort makes the process easier and efficient and hence very much recommended to clearly understand it.