If you study Computer Science, you are bound to come across various algorithms. The Sliding Window Algorithm is one such popular algo, which has its use in cases across fields like computer networks and data communication. In this article, we discuss what the Sliding Window Algorithm technique is and its implementation in Python, C++, and Java.
Problem Statement
Let us first understand the problem before going further with its approach. The problem statement is as follows, find the largest sum of K consecutive entries, given an array of size N. Not sure if you get it? Don’t worry we will understand this by taking an example.
Suppose that the following array is given to us and we are required to find 3 consecutive numbers in this array that give us the largest sum. So, k is equal to 3 in this case.
arr = [16, 12, 9, 19, 11, 8]
Blocks containing three consecutive entries in the given array are [16, 12, 9], [12, 9, 19], [9, 19, 11], [19, 11, 8]. Now we calculate the sum of each block, the sum of each corresponding block is as follows: 37, 40, 39, 38. Out of all these calculated sums, the maximum sum is 40. Therefore, our output is 40.
Naive Approach
There exists an inefficient but simple approach to solving this problem. You may be wondering why are we discussing this approach when it is not efficient enough. Well, one must know the importance of a good approach, right? Also, understanding this approach allows us to build upon the knowledge to allows us to develop a more efficient algorithm called the sliding window algorithm.
In this approach, we begin with the first index and add up until the kth element is reached. For all possible consecutive blocks or groups of k elements, we repeat the process. This approach uses a nested for loop; the outer for loop begins with the first element of the k-element block, and the inner or nested loop continues until the kth element is reached.
As this approach contains two nested loops, therefore, the complexity of this approach is O(N*K). Where n is the size of the array given to us and k is the number of consecutive subentries to be considered. Now what we tell you that this task can be achieved in much less time, can’t believe it? Look for yourself below.
Sliding Window Technique
To understand this approach let us take the help of an analogy. Consider a window of length n and a pane that is fixed in it, of length k. Now, that the pane is originally at the far left, or 0 units from the left. Co-relate the window with the n-element array arr[] and the pane with the k-element current sum.
f we apply force to the window so that it will move a unit distance forward. The following k components will be covered by the pane.
The current sum at each step is calculated by adding the last element of the current block and subtracting the first element of the previous block. That’s it! This is the whole sliding window algorithm. Easy right? Let us now look at the algorithm of this approach.
What is the Sliding Window Algorithm?
The Sliding Window algorithm is a method for finding a subset of elements that satisfy a certain condition in issues. Maintaining a window containing elements from an array or string while advancing the window in a particular direction until the required subset is found is how this method operates.
The fundamental concept is to define the window using two pointers, a left pointer, plus a right pointer. Beginning with the first element of the array or string, both pointers are set to the same value. Then, after moving the right pointer to locate the desired subset, we push the left pointer to enlarge the window until we are no longer able to improve the outcome.
Until the full array or string has been evaluated, this procedure is repeated. When trying to select a subset of elements that satisfy a certain requirement, the sliding window approach comes in handy. The Sliding Window algorithm, for instance, can be used to identify the longest substring, the shortest substring, or the substring with the largest or minimum sum.
Another instance is when we have to determine the highest or lowest sum of a subarray with size k fixed. The Sliding Window technique can be used in this situation to keep a window of k items and slide the window around until that we locate the subset containing the desired sum.
Full Algorithm
Here are the steps for applying the sliding window algorithm:
- Add the first K components together and save the result in the currentSum variable. Because this is the first sum, it is also the current maximum; thus, save it in the variable maximumSum.
- As the window size is K, we move the window one place to the right and compute the sum of the items in the window.
- Update the maximum if the currentSum is greater than the maximumSum, and repeat step 2.
Sliding Window Example
Let us now take an example to understand the algorithm better. Initially, before we start the algorithm, the maximumSum variable is initialized to 0. Also, k is taken as 3 in this example.
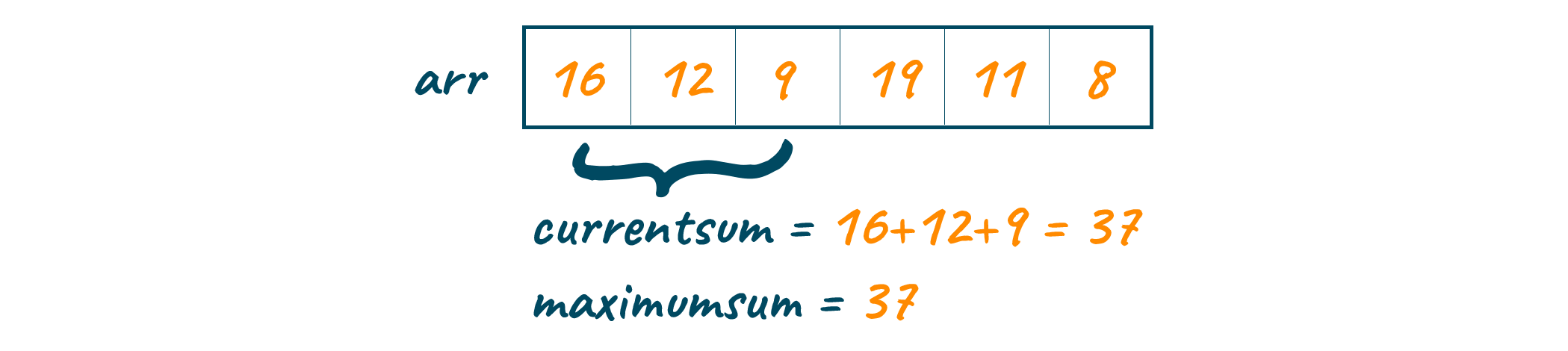
We begin with finding the sum of the first 3 consecutive numbers, i.e., from index 0 to 2. The sum of this initial window comes out to be 37 and is stored in the currentSum variable. Now since the currentSum is greater than maximumSum, therefore, The value of the maximumSum variable is updated to store 37.

The window is slid by a unit distance, to cover the next 3 consecutive numbers. The sum of the new current window is evaluated by subtracting 16 from the currentSum and adding 19 to it. The currentSum is now equal to 40. The latest currentSum value is now compared with the maximumSum since it is greater, therefore, the maximumSum variable will be made to store 40.

The window is again shifted to cover the next 3 consecutive numbers. To get the sum of this window, 12 is deducted from the currentSum and 11 is added which results in 39. As this value is lesser than maximumSum, therefore the value of maximumSum remains unchanged.
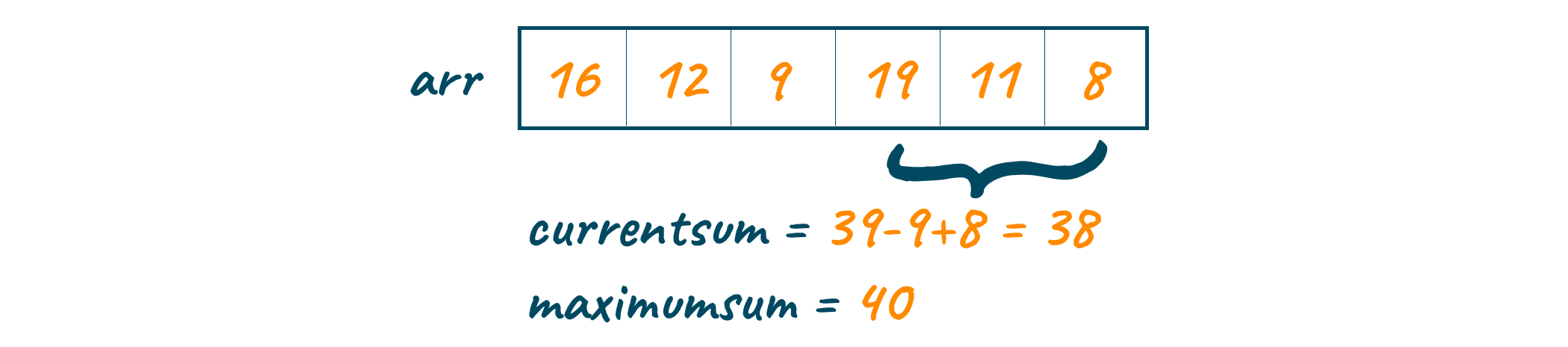
The window now shifts to cover the last 3 consecutive numbers. The sum at this step is evaluated to be equal to 38. As this value is also less than the value of maximumSum (40), its value remains unaffected. All the possible combinations of three consecutive numbers have now been identified and their sums have been evaluated. In the end, the maximumSum, which is identified as 40, is returned.
Python Code for Sliding Window Algorithm
Here is the code to implement Sliding Window Algorithm in Python:
def maxSum(arr, k): # length of the array n = len(arr) # length of array must be greater # window size if n < k: print("Invalid") return -1 # sum of first k elements window_sum = sum(arr[:k]) max_sum = window_sum # remove the first element of previous # window and add the last element of # the current window to calculate the # the sums of remaining windows by for i in range(n - k): window_sum = window_sum - arr[i] + arr[i + k] max_sum = max(window_sum, max_sum) return max_sum arr = [16, 12, 9, 19, 11, 8] k = 3 print(maxSum(arr, k))
C++ Code for Sliding Window Algorithm
Here is the code to implement Sliding Window Algorithm in C++:
#include using namespace std; // Returns maximum sum in a subarray of size k. int maxSum(int arr[], int n, int k) { // n must be greater if (n < k) { cout << "Invalid"; return -1; } //sum of first window of size k int window_sum = 0; for (int i = 0; i < k; i++) window_sum += arr[i]; // Compute sums of remaining windows by // removing first element of previous // window and adding last element of // current window. int max_sum = window_sum; for (int i = k; i < n; i++) { window_sum += (arr[i] - arr[i - k]); max_sum = max(max_sum, window_sum); } return max_sum; } int main(){ int n = 5 , k = 3;; int arr[] = { 16,12,9,19,11,8}; cout << maxSum(arr, n, k); return 0; }
Java Code for Sliding Window Algorithm
Here is the code to implement Sliding Window Algorithm in Java:
public class slidingwindow { static int maxSum(int[] arr,int k){ //length of the array int n=arr.length; //length of array(n) must be greater than window size(k) if(n<k){ System.out.println("Invalid"); return -1; } //sum of first k(window size) elements int window_sum=0; for(int i=0;i<k;i++) window_sum+=arr[i]; int max_sum=window_sum; //Calculating sums of remaining windows by //removing first element of previous window //and adding last element of current window //this way our window moves forward. //Also updating the maximum sum to current window sum // if the current window sum is greater // than existing maximum sum. for(int i=k;i<n;i++){ window_sum+=(arr[i]-arr[i-k]); max_sum=Math.max(window_sum,max_sum); } return max_sum; } public static void main(String[] args) { //window size int k=3; int[] arr={16, 12, 9, 19, 11, 8}; System.out.println(maxSum(arr,k)); } }
Output:
40
Time complexity
The time complexity of the Sliding Window Algorithm is O(N), as in this approach we run only one loop to compute the maximum sum.
What are its Advantages and Disadvantages?
The biggest advantage of the Sliding Window technique is a powerful tool for reducing time complexity and enhancing program performance. Depending on the problem, it can solve ones with linear or logarithmic time complexity.
It is also a memory-efficient algorithm since it only needs a fixed amount of memory. It is appropriate for issues involving huge arrays or strings.
But it also has limited usage. Not all issues are suited for the Sliding Window algorithm. It is only helpful for issues involving locating a subset of items that meet a particular requirement. This algorithm can occasionally be challenging to optimize. To obtain optimal performance, the problem and window size must be carefully taken into account.
Conclusion
The Sliding window Algorithm is a crucial topic for competitive coding. A lot of problems can be solved using this algorithm by doing some small tweaks to it. In this article, we first understood the problem statement, and we then saw the naïve approach. We, at last, learned a more efficient approach along with its code in C++, Java, and Python.
Our experts are available 24/7 for any Live Coding Help you may have.