The initial phases of each established business and startups are dependant on the data of several years. By analyzing the expenses and profit of an organization, we can get insights into the future aspects and prospects of the business growth.
With regression analysis, we can help the finance and investment department in multinational businesses, to not evaluate risks for their company but also analyse the trends in other rival business and use them to their profits. Regression analysis can also help predict sales for a company based on various parameters like GDP growth, previous sales, market growth, or other types of conditions.
What is regression?
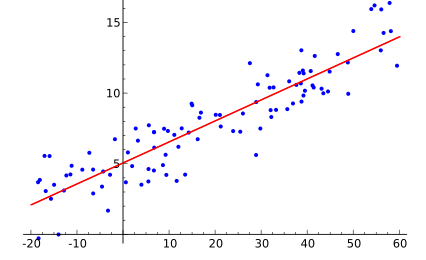
Predictive modelling technique which evaluates the relation between dependent (ie the target variable) and independent variables is known as regression analysis. Regression analysis can be used for forecasting, time series modelling or finding the relation between the variables and predict continuous values. For example, the relation between household regions and the electricity bill of the household by a driver is best studied through regression.
There are two basic types of regression techniques, which are simple linear regression and multiple linear regression, for more complicated data and analysis we use non-linear regression method like polynomial regression. Simple linear regression uses only one independent variable to create the prediction output of the dependent variable Y, whereas multiple linear regression uses two or more independent variables to create prediction outcome.
The general equation of a regression algorithms are as follows:
- Simple linear regression: Y = a + b*X + u
- Multiple linear regression: Y = a + b1*X1 + b2*X2 + b3*X3 + ... + bt*Xt + u
Where:
- Y = Dependent variable
- X = Independent variable
- a = the intercept of regression line.
- b = the slope.
- u = the regression remainder.
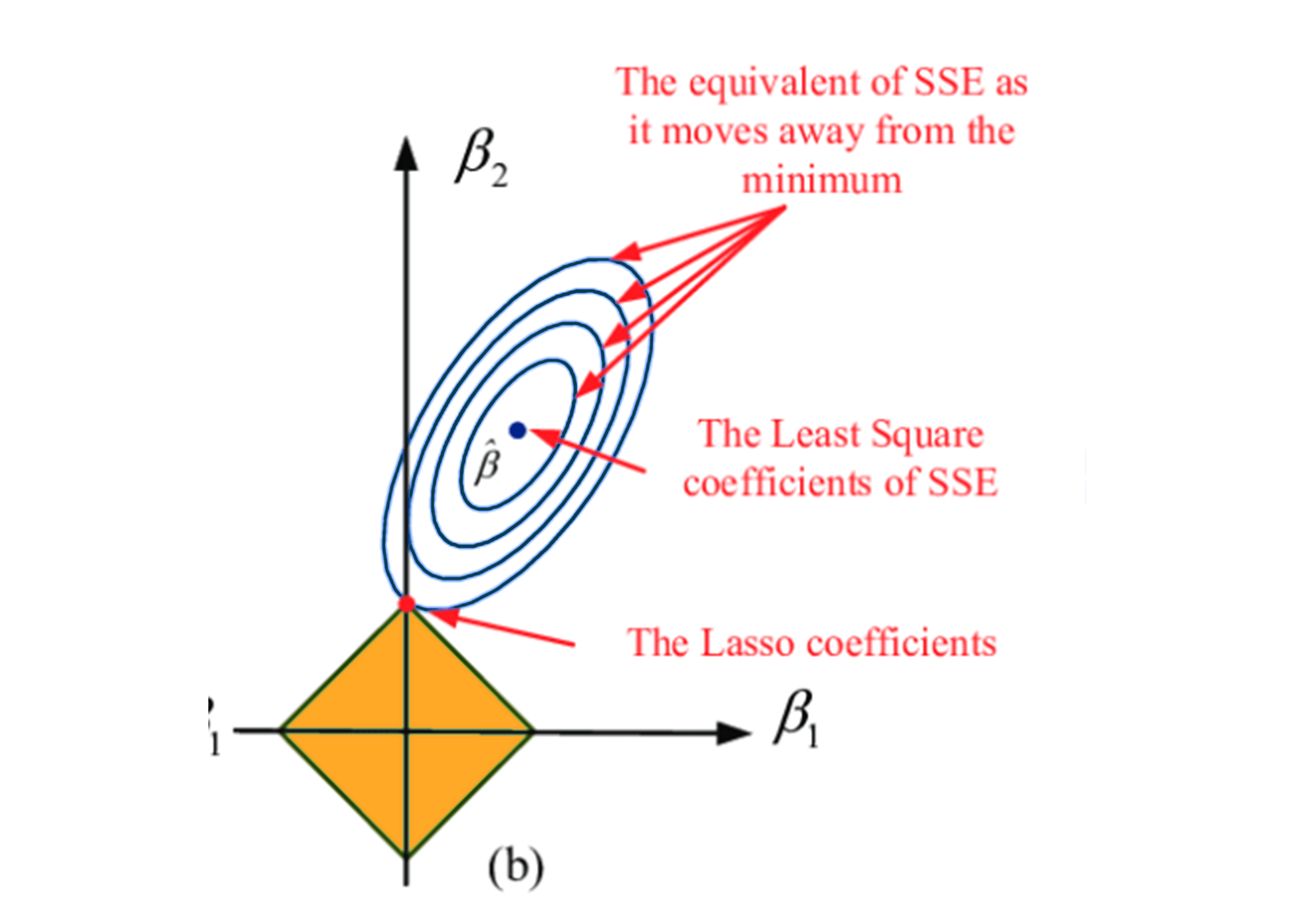
Lasso Regression
The word “LASSO” denotes Least Absolute Shrinkage and Selection Operator. Lasso regression follows the regularization technique to create prediction. It is given more priority over the other regression methods because it gives an accurate prediction. Lasso regression model uses shrinkage technique. In this technique, the data values are shrunk towards a central point similar to the concept of mean. The lasso regression algorithm suggests a simple, sparse models (i.e. models with fewer parameters), which is well-suited for models or data showing high levels of multicollinearity or when we would like to automate certain parts of model selection, like variable selection or parameter elimination using feature engineering.
Lasso Regression algorithm utilises L1 regularization technique It is taken into consideration when there are more number of features because it automatically performs feature selection.
Mathematical equation of Lasso Regression Algorithm:
Residual Sum of Squares + λ * (Sum of the absolute value of the coefficients)
The equation looks like:
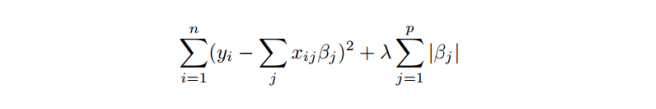
Where,
- λ = the amount of shrinkage.
- If λ = 0 it implies that all the features are considered and now it is equivalent to the linear regression in which only the residual sum of squares is used to build a predictive model.
- If λ = ∞ it implies that no feature is used i.e, as λ gets close to infinity it eliminates more and more features and feature selection is more precise.
- When the bias increases, the value of λ increases
- When the variance increases, the value of λ decreases
Lasso Regression Implementation in Python using sklearn
from sklearn.linear_model import Lasso lassoReg = Lasso(alpha=0.3, normalize=True) lassoReg.fit(x_train,y_train) pred = lassoReg.predict(x_cv) # calculating mse mse = np.mean((pred_cv - y_cv)**2)
Ridge Regression
Ridge Regression is another type of regression algorithm in data science and is usually considered when there is a high correlation between the independent variables or model parameters. As the value of correlation increases the least square estimates evaluates unbiased values. But if the collinearity in the dataset is very high, there can be some bias value. Therefore, we create a bias matrix in the equation of Ridge Regression algorithm. It is a useful regression method in which the model is less susceptible to overfitting and hence the model works well even if the dataset is very small.
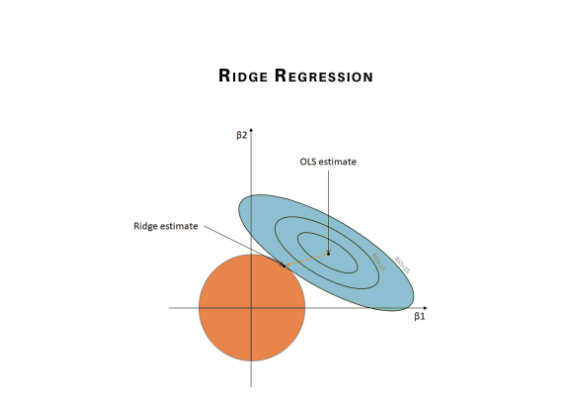
The cost function for ridge regression algorithm is:
Where λ is the penalty variable. λ given here is denoted by an alpha parameter in the ridge function. Hence, by changing the values of alpha, we are controlling the penalty term. Greater the values of alpha, the higher is the penalty and therefore the magnitude of the coefficients is reduced.
We can conclude that it shrinks the parameters. Therefore, it is used to prevent multicollinearity, it also reduces the model complexity by shrinking the coefficient.
Bias and variance trade-off
Bias and variance trade-off is a complicated algorithm when we try to build ridge regression models on an actual dataset with multiple features. However, following the general trend which we can take note of are:
- When the bias increases, the value of λ increases
- When the variance increases, the value of λ decreases
Ridge Regression Implementation in Python using sklearn
from sklearn.linear_model import Ridge ## training the model ridgeReg = Ridge(alpha=0.05, normalize=True) ridgeReg.fit(x_train,y_train) pred = ridgeReg.predict(x_cv) calculating mse mse = np.mean((pred_cv - y_cv)**2) print(mse) ## calculating score score = ridgeReg.score(x_cv,y_cv) print(score)
Comparative Analysis of Lasso and Ridge Regression
Ridge and Lasso regression uses two different penalty functions for regularisation. Ridge regression uses L2 on the other hand lasso regression go uses L1 regularisation technique. In ridge regression, the penalty is equal to the sum of the squares of the coefficients and in the Lasso, penalty is considered to be the sum of the absolute values of the coefficients. In lasso regression, it is the shrinkage towards zero using an absolute value (L1 penalty or regularization technique) rather than a sum of squares(L2 penalty or regularization technique).
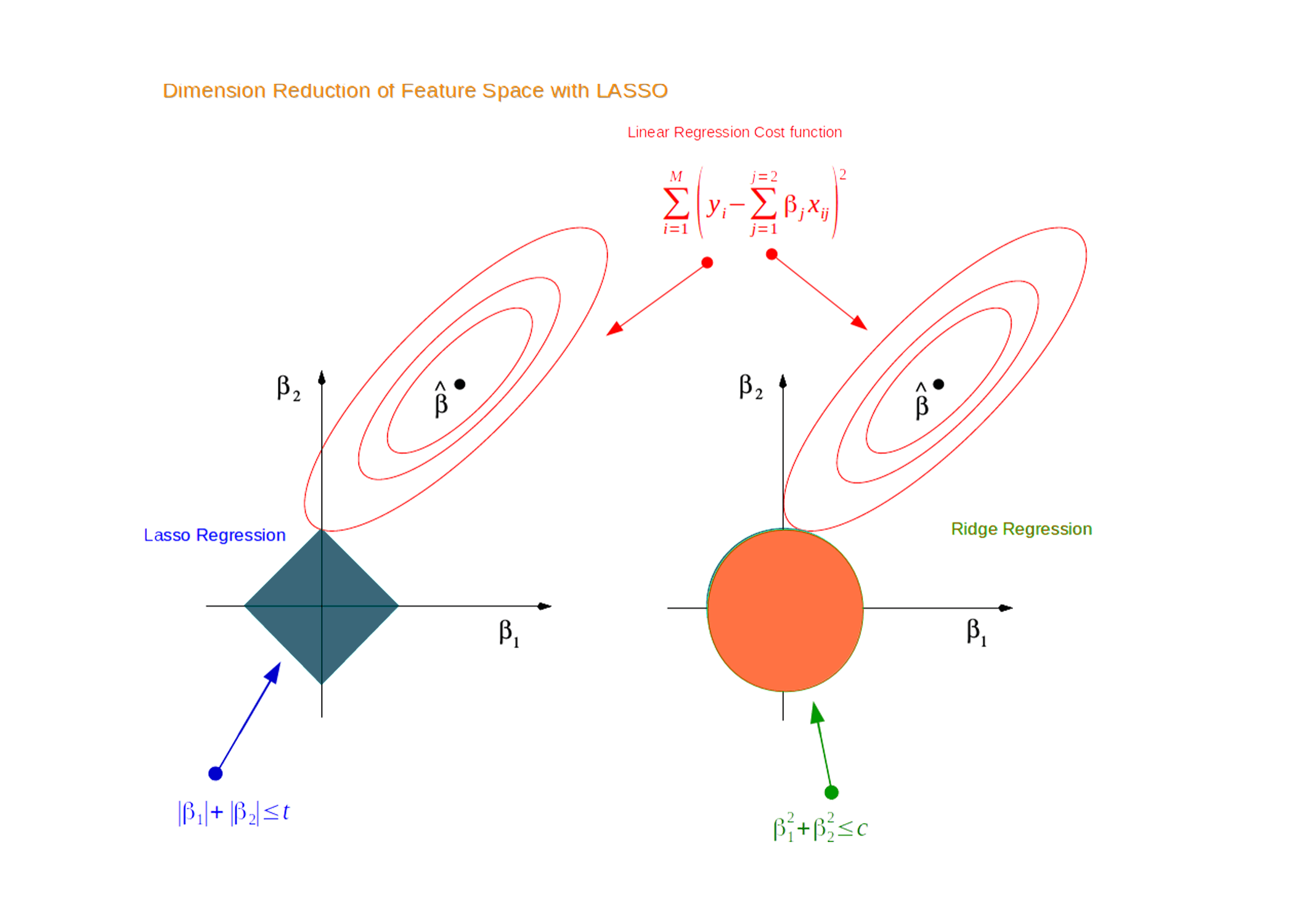
Since we know that in ridge regression the coefficients can’t be zero. Here, we either consider all the coefficients or none of the coefficients, whereas Lasso regression algorithm technique, performs both parameter shrinkage and feature selection simultaneously and automatically because it nulls out the co-efficients of collinear features. This helps to select the variable(s) out of given n variables while performing lasso regression easier and more accurate.
There is an another type of regularization method, which is ElasticNet, this algorithm is a hybrid of lasso and ridge regression both. It is trained using L1 and L2 prior as regularizer. A practical advantage of trading-off between the Lasso and Ridge regression is that it allows Elastic-Net Algorithm to inherit some of Ridge’s stability under rotation.
Conclusion
Therefore, in this tutorial we got a better understanding of lasso and ridge regression and the mathematical part of the algorithm with implementation using a sample dataset. We also learned comparative analysis of the algorithm.


.png)





