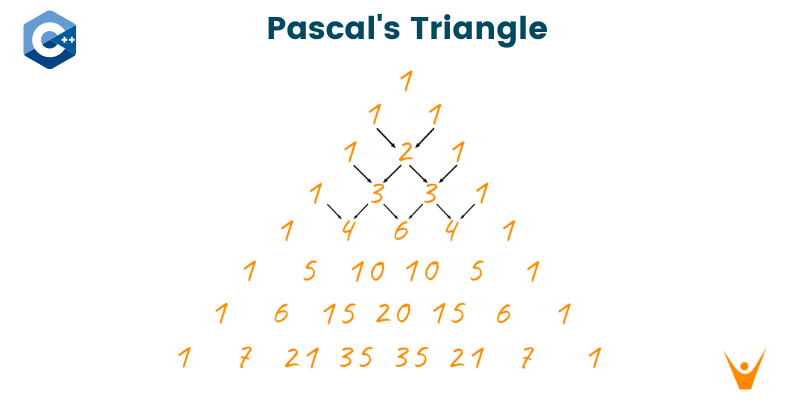
Even if you are just a beginner at coding, then also, you must have come across problems like printing triangles like a half pyramid, inverted half pyramid, and full pyramid using some characters. One variation of the above-mentioned problems is Pascal’s Triangle. In this article, we will discuss what is pascal’s triangle and its implementation in C++.
But before continuing, we expect that you have a basic understanding of conditional statements and looping.
What is Pascal's Triangle?
Pascal’s Triangle is named after a French Mathematician called Blaise Pascal. It is a triangle made up of numbers organized in a certain manner. The triangle is built using an additive principle. What do we mean by additive principle? Well, Every number inside the triangle is obtained by summing up the above two adjacent elements (this will be clearer after seeing the image below). This rule of obtaining new elements of a pascal’s triangle is applicable to only the inner elements of the triangle and not to the elements on the edges. These elements on the edges, except that of the base, of the triangle are equal to 1.
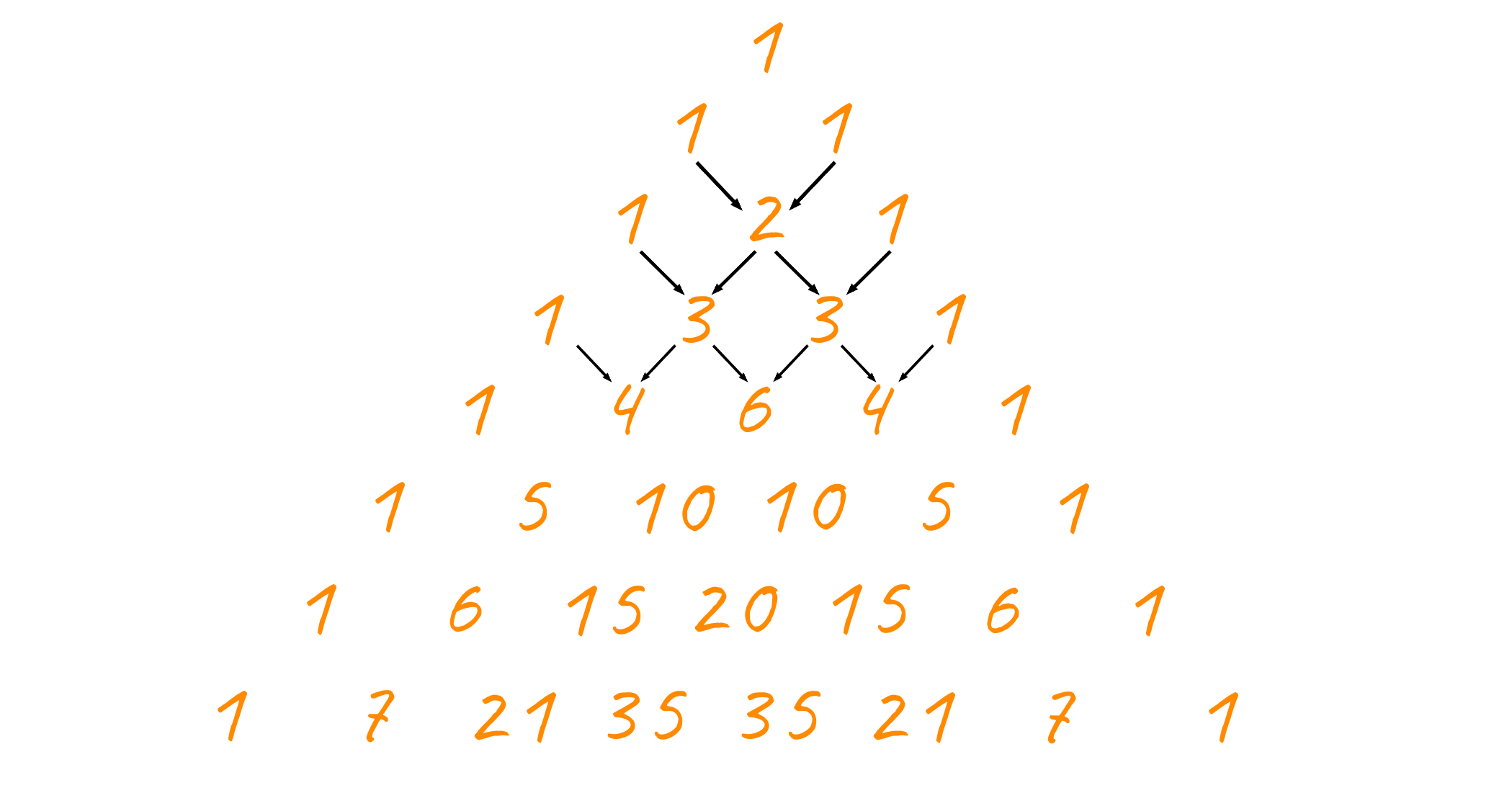
Now that we know what Pascal's triangle is, let us now discuss one of its most important mathematical properties which will help us in implementing Pascal's triangle via code. If you have a little mathematical background then must be familiar with the concept of permutations and combinations. The number of ways certain objects can be chosen from a group of objects is known as combinations.
What is Pascal's Triangle Formula?
The formula for calculating the number of ways in which r objects can be chosen from n objects is given below
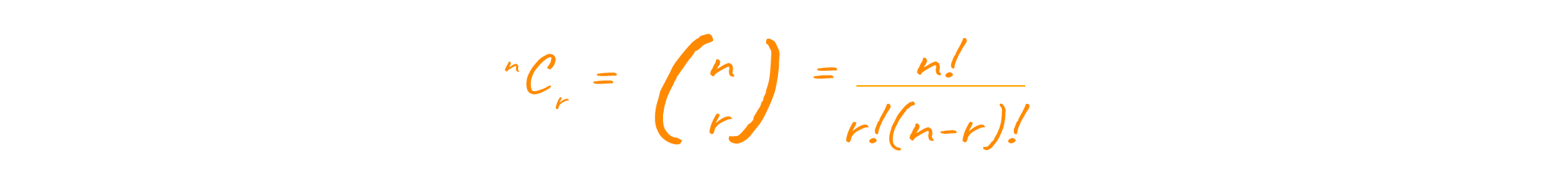
Now, hold tight because you are going to be amazed by this fact. Each element in Pascal's Triangle can be calculated using the element's row and column number. For example, the value of the element in the third row and second columns will be equal to 2C1, which is 2. Note how the row and column numbers are subtracted by 1 while calculating the value. This is because counting in programming starts from 0 and not from 1. Look at the image below, to have a clearer understanding.
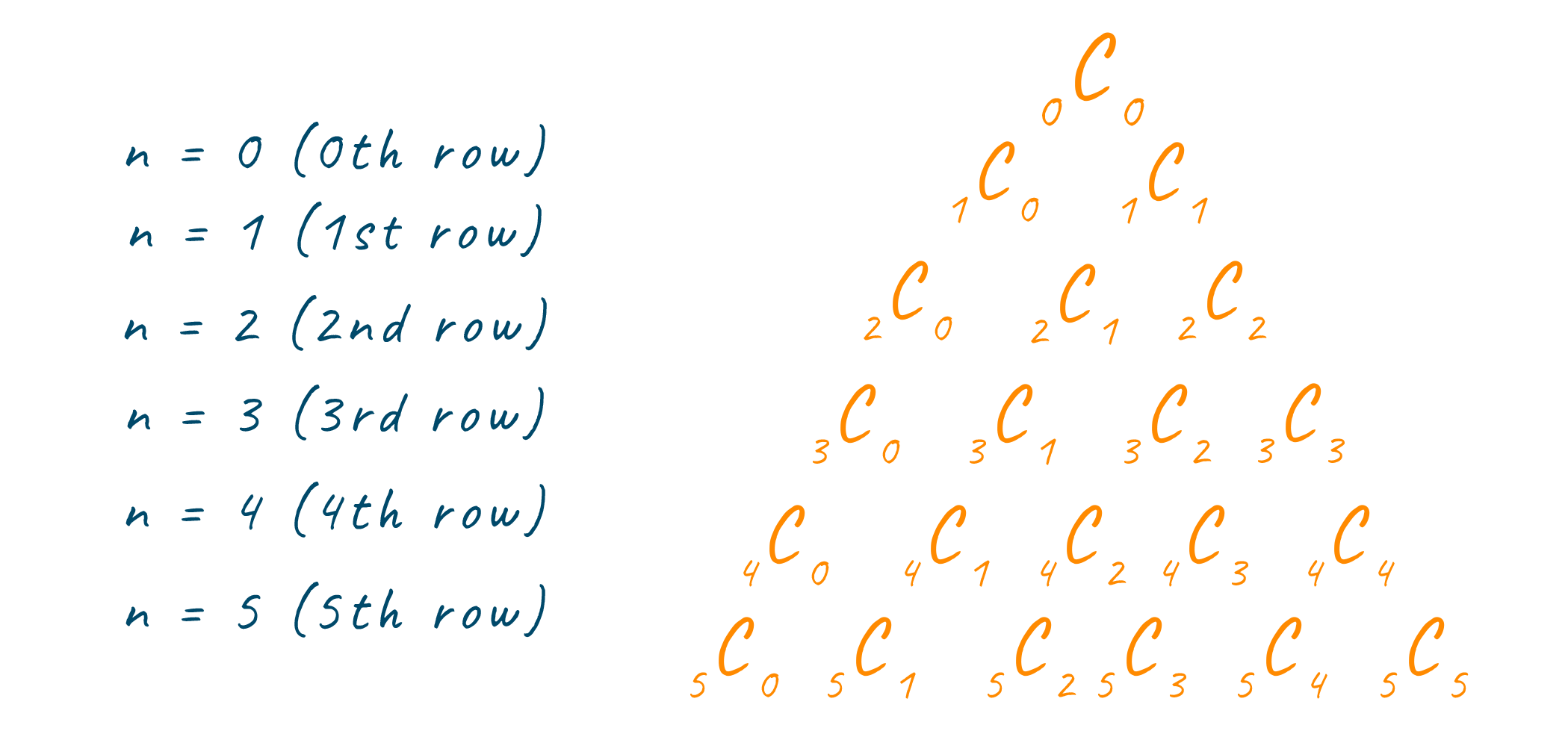
This can also be understood using binomial expansions. Because each binomial coefficient is equal to a value in Pascal’s Triangle. Now, that we understand what is pascals triangle and its combinatorics property, we will use this property to code.
How to Print Pascal's Triangle in C++ Programming?
If you have been coding even for a while, you must implement several triangular patterns using conditional and looping statements. Pascal’s triangle implementation is similar with a few alterations.
For implementation, we make use of nested looping. The outer loop works for getting the row indentation. The first loop inside the outer loop creates proper indentation using spaces so that we get a triangular display. The second loop inside the outer loop calculates the value of the current element using the value of the previous element with the help of the following formula:
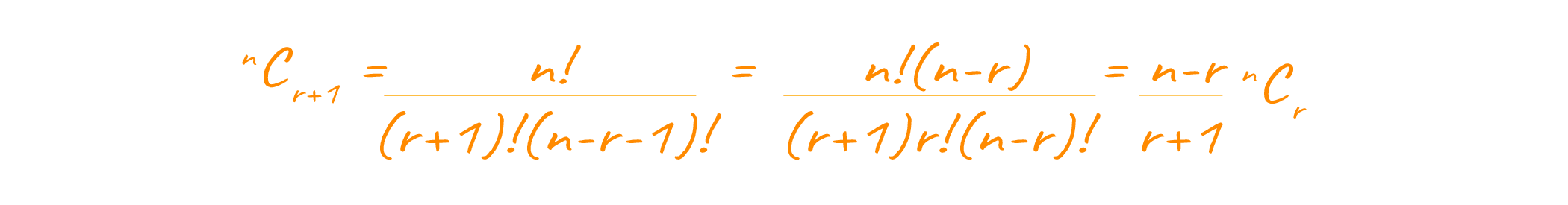
All this happens inside a function responsible for printing the pascals triangle, and it takes only one argument which is the number of rows to be printed of the pascal’s triangle.
C++ Code for Pascal's Triangle
#include using namespace std; // Function to print the Pascal's Triangle void print_pascal(int row_num){ // Loop to print each row for(int n = 1; n <= row_num; n++){ // Loop to print spaces for triangular display for(int r = 1; r < row_num-n+1; r++) cout<<" "; // Loop to print values using the Combinations formula int val = 1; for(int r = 1; r <= n; r++){ cout<<val<<" "; val = val * (n - r)/r; } cout<<endl; } } int main(){ int row_num = 8; print_pascal(row_num); return 1; }
Output
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Time complexity
This algorithm is efficient and requires O(n2) time because of nested looping.
Space Complexity
This algorithm doesn’t require any auxiliary space and therefore has a space complexity of O(n).
Conclusion
Problems like these develop one’s mind for problem-solving and hence making him or her a better problem solver. If you found Pascal’s Triangle a little hard to understand, we recommend you to first look at printing the full pyramid and then come back and give pascals triangle one more try. Another point that we want to bring to your attention is that Pascal's triangle can be printed using several different approaches, but in this article, we have discussed only the most efficient one along with its code in C++.
To sharpen your competitive and DSA skills, try this Palindrome Pairs Problem.