Every engineering student aspires to get a decent placement, but the journey to that goal isn’t very easy for most of us. There are so many technical interview questions, one of which we will understand today. Learn how to check if a String is a Palindrome or not using C++.
How to Check if a Linked List is Palindrome?
This particular problem statement has been asked in technical interviews with many multinational companies like Google, Facebook, and Uber. Let’s understand first what exactly is a palindrome.
A palindrome number is a number or a string that is equivalent to the string or number after reversing the string/number. For example, 12321, 565, 23432, 141, etc are the palindrome numbers. A palindrome can also be a string like MOM, MADAM, LOL, etc.
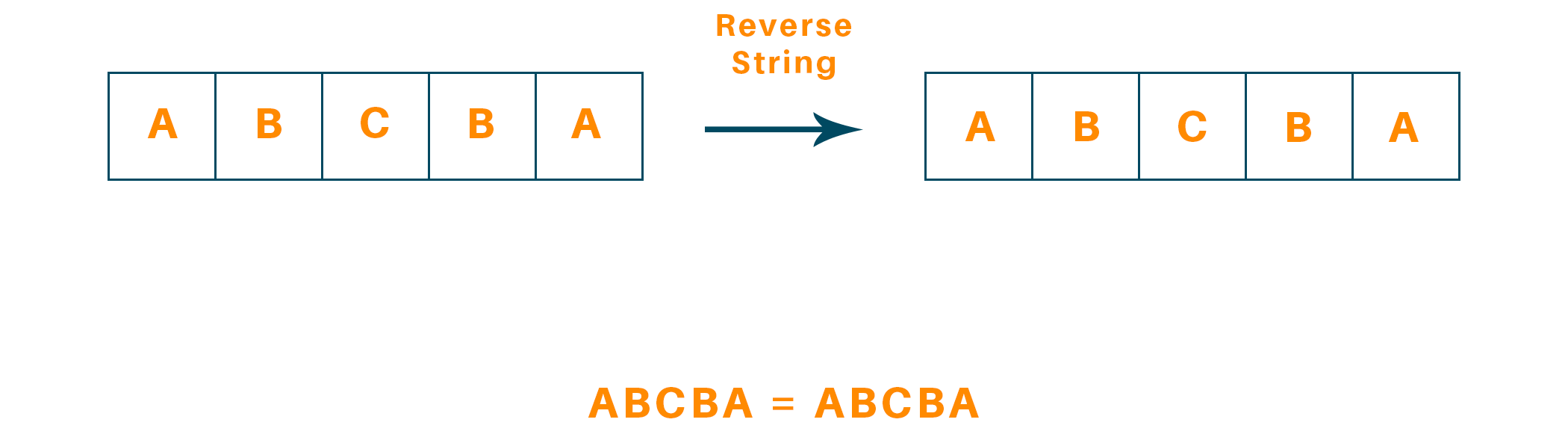
Let’s discuss the problem statement: "We are given the head of a singly linked list of characters, write a function which returns a boolean value that indicates true if the given linked list is a palindrome, else false."
Now here is an example to better understand it.
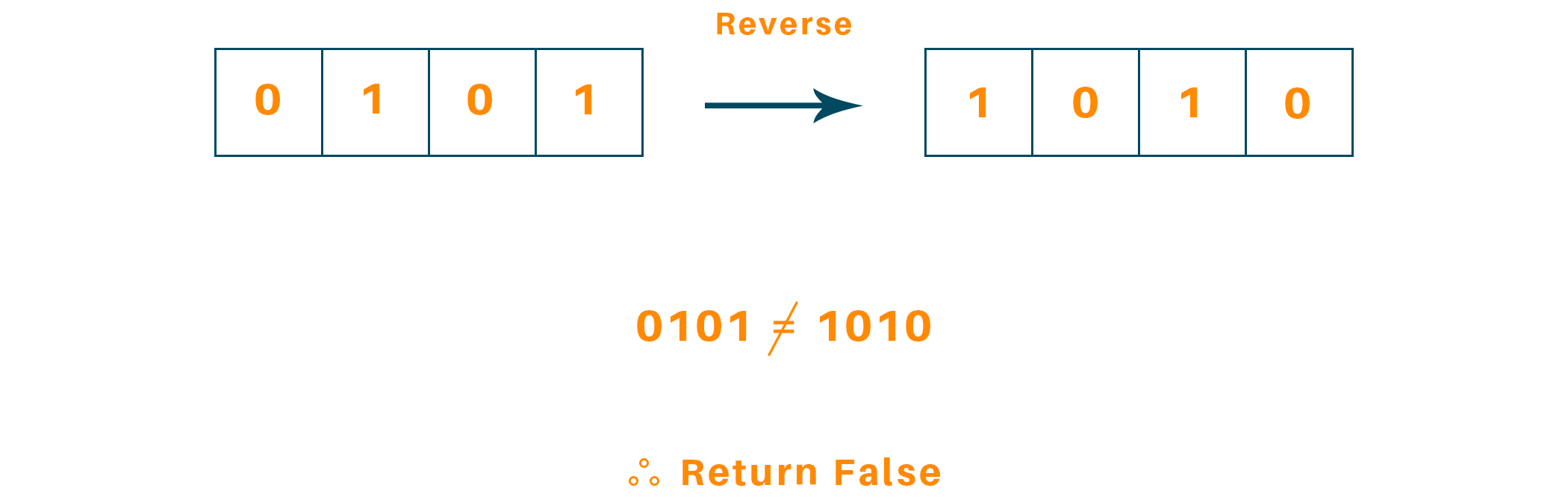
The function will return it’s not a palindrome.
There are two approaches to solve this problem, one involves the use of stack data structure and the other involves reversing the list and verifying the occurrence of the elements. There is one more approach to solving this problem using a recursive function call. Let’s discuss the algorithms!
6 Ways to Check Linked List is Palindrome
There are 6 different ways available in programming to check whether a given linked list is a palindrome or not. Let's learn them one by one.
1) Using Stack
In this algorithm, we use a stack of list elements. There are three operations needed to be formed to implement our algorithm.
- Iterate through all the elements in the given list from the head pointer to the tail and push every element to the stack as we traverse.
- Now we traverse the list again. And at each node, we pop an element from the stack and compare the element in the popped node with the current node.
- If all the nodes match, then we return the boolean value true, or else return false.
Here is the C++ program for this method:
#include<bits/stdc++.h> using namespace std; // Declaration of a single Node class Node { public: int data; Node(int d){ data = d; } Node *ptr; }; // Function that returns boolean value bool isPalin(Node* head){ // Temp pointer Node* slow= head; // Create a stack stack <int> s; // First traversal to push all the elements to stack while(slow != NULL){ s.push(slow->data); slow = slow->ptr; } // Second Traversal to compare the stack and node while(head != NULL ){ int i=s.top(); s.pop(); // Compare data if(head -> data != i){ return false; } head=head->ptr; } return true; } // Driver Function int main(){ // Create nodes Node one = Node(31); Node two = Node(32); Node three = Node(33); Node four = Node(34); Node five = Node(35); // Connect all the nodes five.ptr = NULL; one.ptr = &two; two.ptr = &three; three.ptr = &four; four.ptr = &five; Node* temp = &one; // Call function to return bool if the list is palindrome or not int result = isPalin(&one); if(result == 1) cout<<"The value is True\n"; else cout<<"The value is False\n"; return 0; }
Output:
The value is not a palindrome.
The time complexity of the algorithm is O(N) because we iterate through each element at least once. As we push the elements into the stack one by one we are bound to iterate over the complete linked list at least once and therefore the time complexity of the algorithm is O(N) and since we are using a stack to push all the elements, the space complexity of the algorithm is also O(N).
2) Reversing the list
In this algorithm, we simply reverse half of the linked list. There are four operations needed to be formed to implement our algorithm.
- Find the middlemost element of the linked list.
- Then we reverse the second half of the linked list.
- We verify if the first half and second half are equivalent by comparing node by node.
- Then we reconstruct the original linked list by inverting the second half once more and attaching it back to the first half
We divide this list into halves by keeping the count if the count variable is even, and then the first and second halves would exactly have half elements, and in case of an odd number of elements we use a variable ‘midnode’. Below is the C++ code to implement it:
#include<bits/stdc++.h> using namespace std; struct ListNode { int val; ListNode *next; ListNode() : val(0), next(nullptr) {} ListNode(int x) : val(x), next(nullptr) {} ListNode(int x, ListNode *next) : val(x), next(next) {} }; // Function to find the mid of linked-list ListNode* find_middle(ListNode* head,int n) { ListNode *slow=head,*fast=head; while(fast!=NULL && fast->next!=NULL) { slow=slow->next; fast=fast->next->next; } if(n&1) return slow->next; else return slow; } // Function to Reverse the List using three pointers ListNode* reverse_link(ListNode* head) { ListNode *prev=NULL; ListNode *curr=head; ListNode *next=NULL; while(curr!=NULL) { next=curr->next; curr->next=prev; prev=curr; curr=next; } return prev; } // Return if the Linked List is palindrome bool isPalindrome(ListNode* head) { if(head==NULL || head->next==NULL) return true; ListNode *temp=head; // Iterate to count odd/even int n=0; while(temp!=NULL) { temp=temp->next; n++; } temp=head; // Find the mid elemeny ListNode *head_mid=find_middle(temp,n); // Reverse the second half linked-list ListNode *head_rev=reverse_link(head_mid); // Verify first half and second half of linked-list are equivalent while(head_rev!=NULL) { if(head->val!=head_rev->val) return false; head_rev=head_rev->next; head=head->next; } return true; } // Driver Function int main(){ // Create nodes ListNode one = ListNode(31); ListNode two = ListNode(32); ListNode three = ListNode(33); ListNode four = ListNode(32); ListNode five = ListNode(31); ListNode *one_ptr = &one; ListNode *two_ptr = &two; ListNode *three_ptr = &three; ListNode *four_ptr = &four; ListNode *five_ptr = &five; // Connect all the nodes five_ptr->next = NULL; one_ptr->next = &two; two_ptr->next = &three; three_ptr->next = &four; four_ptr->next = &five; ListNode* temp = &one; // Call function to return bool if the list is palindrome or not int result = isPalindrome(&one); if(result == 1) cout<<"The value is Palindrome\n"; else cout<<"The value is NOT Palindrome\n"; return 0; }
Output:
The value is palindrome.
The time complexity of this algorithm is O(N) because we iterate through each of the elements in the linked list at least half the time. As we divide the linked list into two halves and keep the count of the variable and check if it is even, hence the time complexity is O(N). The space complexity of the algorithm is O(1) because we don’t use any extra space to find the outcome.
4) Recursion
The recursive method to check for palindromes in a linked list involves examining the linked list's first and last members. If they match, those entries are removed and the procedure with the remaining linked list is called recursively. The process is repeated until the linked list is empty or we come across an unrelated pair of entries.
Here is the C++ code to determine whether a singly linked list contains a palindrome:
bool isPalindromeRecursiveHelper(ListNode* &left, ListNode* right) { if (right == nullptr) { return true; } bool isPal = isPalindromeRecursiveHelper(left, right->next); if (!isPal) { return false; } isPal = (left->val == right->val); left = left->next; return isPal; } bool isPalindromeRecursive(ListNode* head) { return isPalindromeRecursiveHelper(head, head); }
The helper method isPalindromeRecursiveHelper in this code accepts two pointers, left and right. The right initially points to the final element of the linked list, while the left initially points to the linked list's head. If the linked list contains a palindrome, the function returns true; if not, it returns false.
5)Extra Data Structure
This strategy involves building a stack and pushing the first portion of the linked list onto it. Then, we iterate across the linked list's second half and compare each entry to the stack's top element. The linked list is a palindrome if every entry matches.
Here is some C++ code that uses an additional data structure:
bool isPalindromeStack(ListNode* head) { stack<int> s; ListNode* slow = head; ListNode* fast = head; while (fast != nullptr && fast->next != nullptr) { s.push(slow->val); slow = slow->next; fast = fast->next->next; } if (fast != nullptr) { slow = slow->next; } while (slow != nullptr) { if (s.top() != slow->val) { return false; } s.pop(); slow = slow->next; } return true; }
In this code, the linked list is iterated over using two pointers, slow and fast. Fast moves two steps in a single motion, while slow moves one. Until fast reaches the end of the linked list, we push the elements slowly pointed onto the stack. We omit the middle element if the linked list contains an odd number of elements.
Then, we make a comparison between the linked list's remaining elements and those on the stack. The linked list is a palindrome if they coincide.
6) Reversing the Second Half
This method's goal is to discover the center element by repeatedly iterating through the linked list. After that, we compare the first and second halves of the linked list in reverse. The linked list is a palindrome if they coincide.
Below is the C++ function to implement it:
bool isPalindromeReverse(ListNode* head) { if (head == nullptr || head->next == nullptr) { return true; } ListNode* slow = head; ListNode* fast = head; while (fast != nullptr && fast->next != nullptr) { slow = slow->next; fast = fast->next->next; } ListNode* prev = nullptr; ListNode* cur = slow; while (cur != nullptr) { ListNode* next = cur->next; cur->next = prev; prev = cur; cur = next; } ListNode* p1 = head; ListNode* p2 = prev; while (p2 != nullptr) { if (p1->val != p2->val) { return false; } p1 = p1->next; p2 = p2->next; } return true; }
To locate the middle element of the linked list, this code makes use of two pointers, slow and fast. Fast moves two steps in a single motion, while slow moves one. Slow identifies the middle element when fast reaches the end of the linked list.
Then, by iterating from slow through the end of the linked list and switching the orientation of the pointers, we reverse the second half of the linked list. The previous element is tracked using prior, the current element is tracked using cur, and the next element is tracked using next.
Finally, we compare each member after iterating through the first half of the linked list (p1) and the inverted second half (p2). The linked list is a palindrome if they coincide.
Conclusion
In this tutorial, we discussed the definition of a palindrome and how can we check if the linked list is a palindrome or not using two approaches and discussed its code in C++. We observed that both approaches have a time complexity of O(N) whereas if we use the second approach ie reversing the list takes less space as compared to the first approach.