Painters partition problem is a classic programming problem, that will force you to think out of the box and you will get to know about the other scenarios in which binary search can be implemented.
Painters Partition Problem Statement
Here is the problem statement for Painter Partition Problem: "N boards of length [A1, A2, A3.........AN] are to be painted by K painters available and each of them takes 1 unit of time to paint 1 unit of board. We need to find minimum time to get these boards painted with some given constraints."
These constraints are:
- No 2 painters can share a board to paint. That implies a board can't be printed partially by one painter and partially by another.
- A painter can only paint contiguous boards. That is, a painter can paint boards 1 and 2 but can't paint boards 1 and 3.
Approach Using Binary Search
Given an array describing the length of boards and the number of painters. Let's start by analyzing the least possible time taken by painters i.e. max element of the array, this can be only possible if we have painters = arr.length, each painter to paint each board.
And if we take painter = 1, we get the max Possible time i.e. the sum of all array elements. From this, we can notice that on the right, the number of painters decreases and on the left, they increase.
- First, we try to find the mid between the least and max time.
- Now we count the minimum number of painters needed to paint the whole board when the max units of time one painter can have is mid.
- We find the number of painters by taking max time as the total time allotted to each painter and as the sum of array elements exceeds this, we increase the painter count by 1, and if that painter also exceeds the maxTime we increase the count of painters.
- Now the main condition to discard any part would be, if the count of painters is greater than the painters provided, we move right and discard the left part.
- If the count of painters is less than the number of painters provided or equal, we move to the left and discard the right in search of a more potential answer.
Following is the Java code to solve Painters Parition Problem:
public class PaintersPartitionProblem { public static void main(String[] args) { int [] arr = {5, 25, 30, 20, 15}; int k = 3; int minimumTime = paintersPartitionProblem(arr, k); System.out.println("Minimum time needed for painters to paint the board : " + minimumTime); } public static int paintersPartitionProblem(int [] arr, int k) { //initializing low and high as max element of array and sum of all elements of array respectively. int lo = maxElement(arr); int hi = sumOfElements(arr); //this is our answer keeping track of minimum time needed. int minTime = Integer.MAX_VALUE; //implementing binary search while( lo <= hi) { int mid = (lo + hi)/2; //finding the painters needed to paint the boards if mid is maxTime. int paintersNeeded = numberOfPainters(arr, arr.length, mid); //if paintersNeeded > provided number of painters, we move right. if(paintersNeeded > k) { lo = mid + 1; }else { //if painters is less than or equal to provided painters at mid, that implies this can be out potential answer //so we store this and move to left part to search for a better answer. minTime = mid; hi = mid - 1; } } return minTime; } public static int sumOfElements(int[] arr) { int sum = 0; for(int i = 0 ;i < arr.length; i++) { sum += arr[i]; } return sum; } public static int maxElement(int[] arr) { int max = Integer.MIN_VALUE; for(int i = 0; i < arr.length; i++) { if(arr[i] > max) max = arr[i]; } return max; } public static int numberOfPainters(int[] arr, int n, int maxTime) { // initially taking painters to be 1. int paintersNeeded = 1; // to keep a check that time doesn't exceed the maxTime provided. int totalTime = 0; for(int i = 0; i < arr.length; i++) { totalTime += arr[i]; // if total time exceeds max time that implies the same painter can't paint more boards // so we increase the painters needed, and initialize total time as arr[i]. if(totalTime > maxTime) { paintersNeeded++; totalTime = arr[i]; } } return paintersNeeded; } }
Output:
Minimum time needed for painters to paint the board : 35
Example with Illustration
Given an array arr = {10, 20, 30, 40} painter s = 2;
Iteration 1
The lowest time for painters can be 40, as it is the max element and the highest time for painters can be 100, the sum of all elements of the array. The mid comes out to be 70.
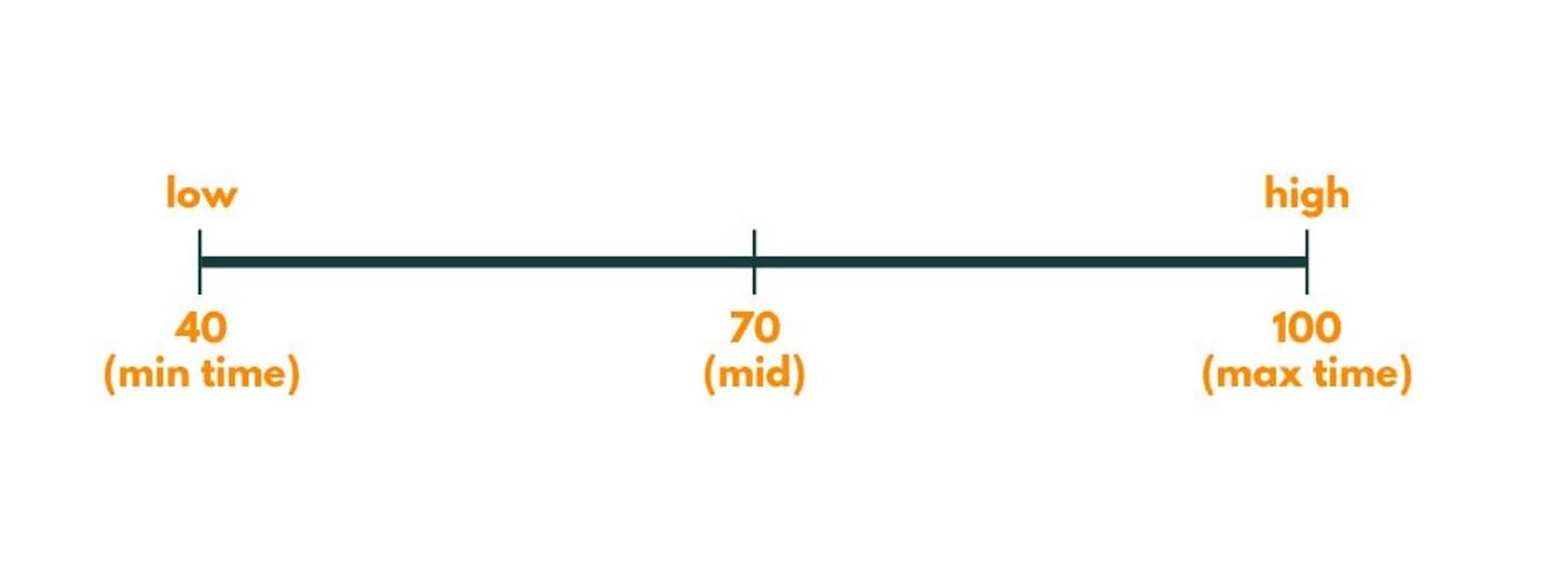
The painters needed are 2. As it can be our potential answer, we store it as minimum time and try to find a better answer. So we discard the right part and put high = 69 (mid - 1).
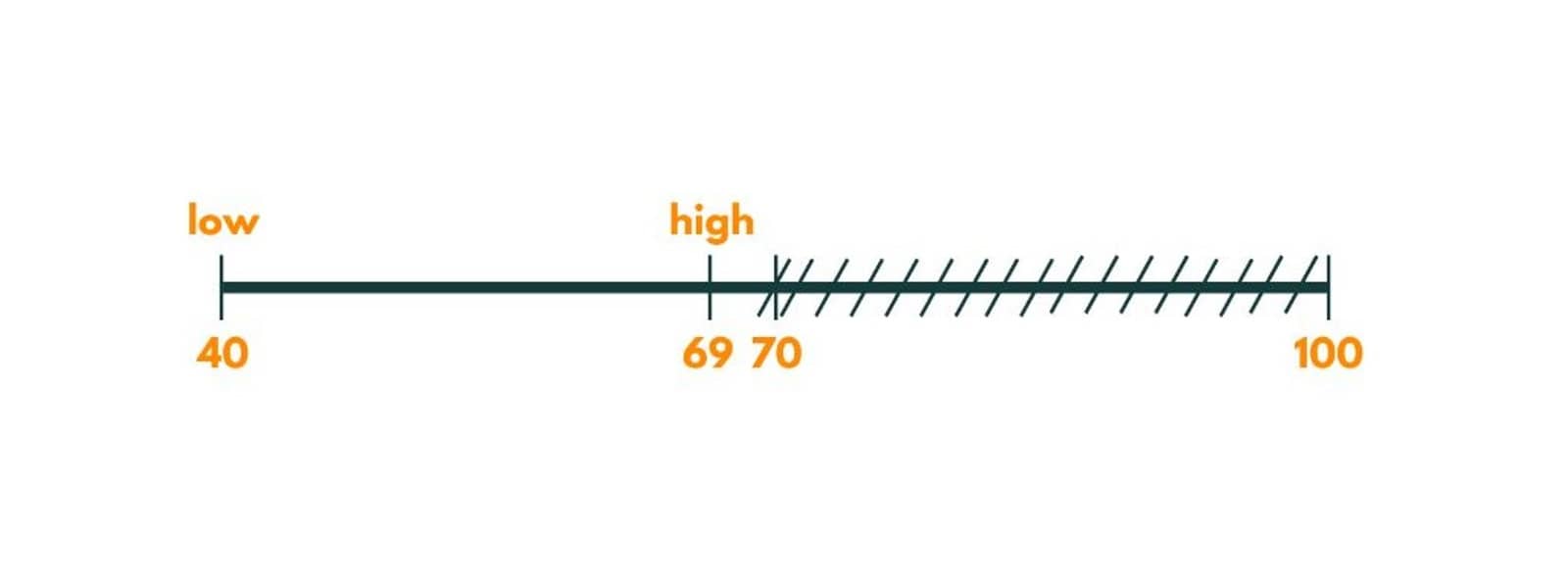
Iteration 2
Now, the mid comes out to be 54.
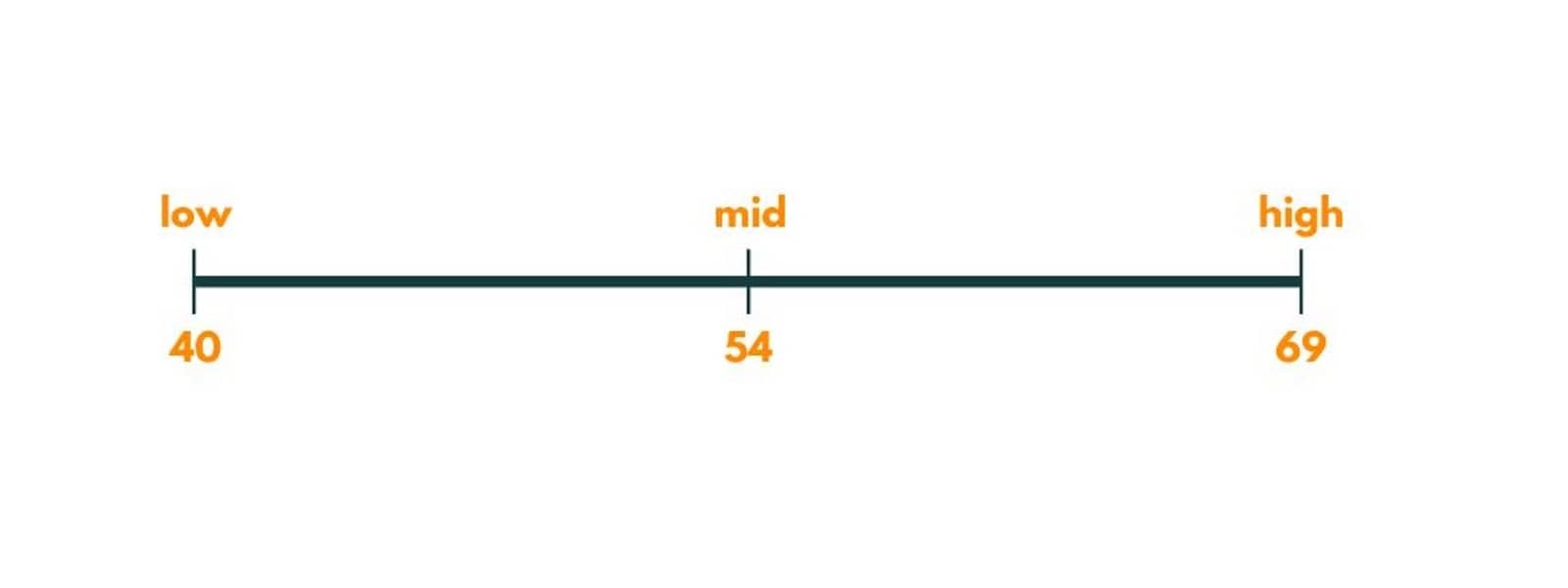
The painters needed with a maximum time of 54 would be 3, which is greater than the number of painters provided. So we move towards the right by putting a low as 55 (mid +1).
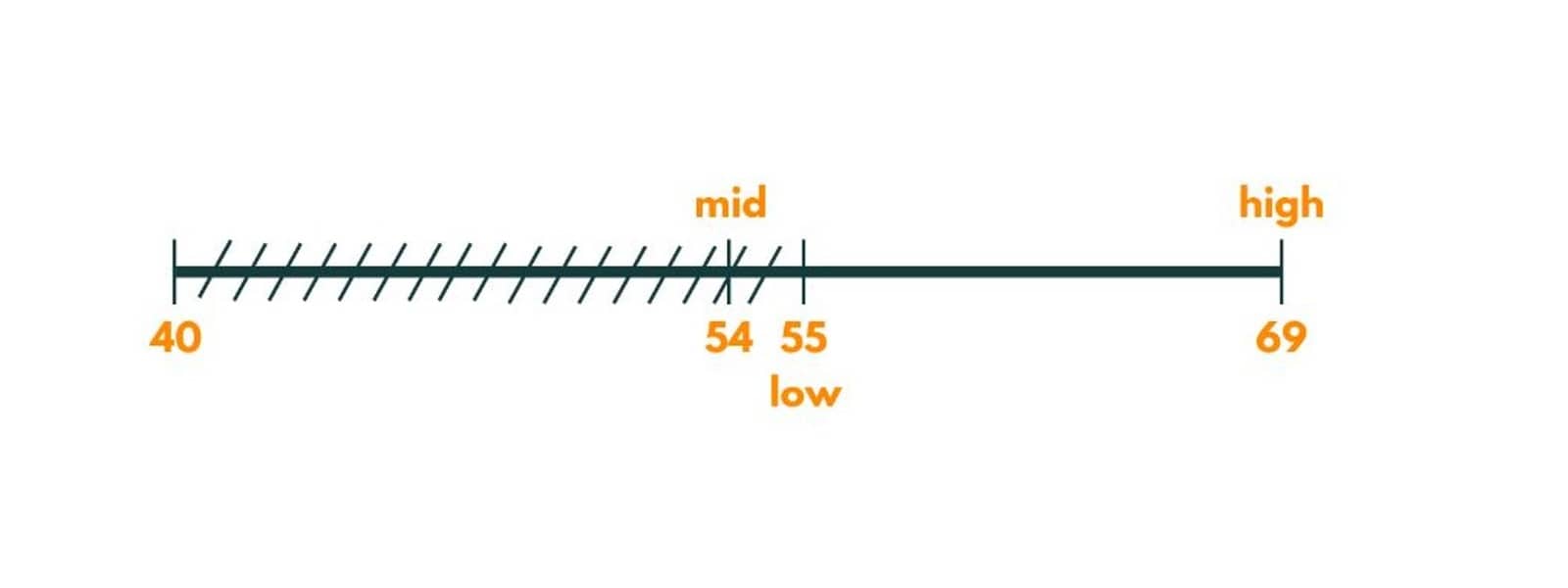
Iteration 3
The mid here is 62.
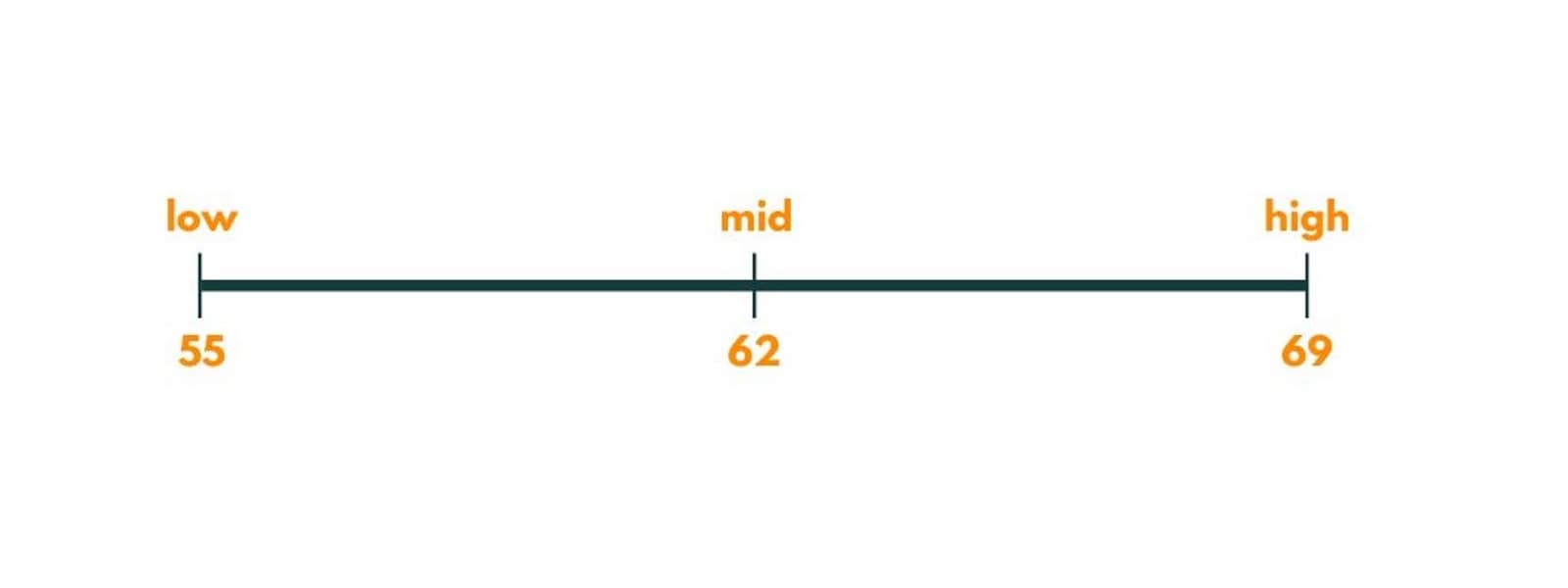
The painters needed would be 2 with a maximum time of 62. So we move left and put high as 61.
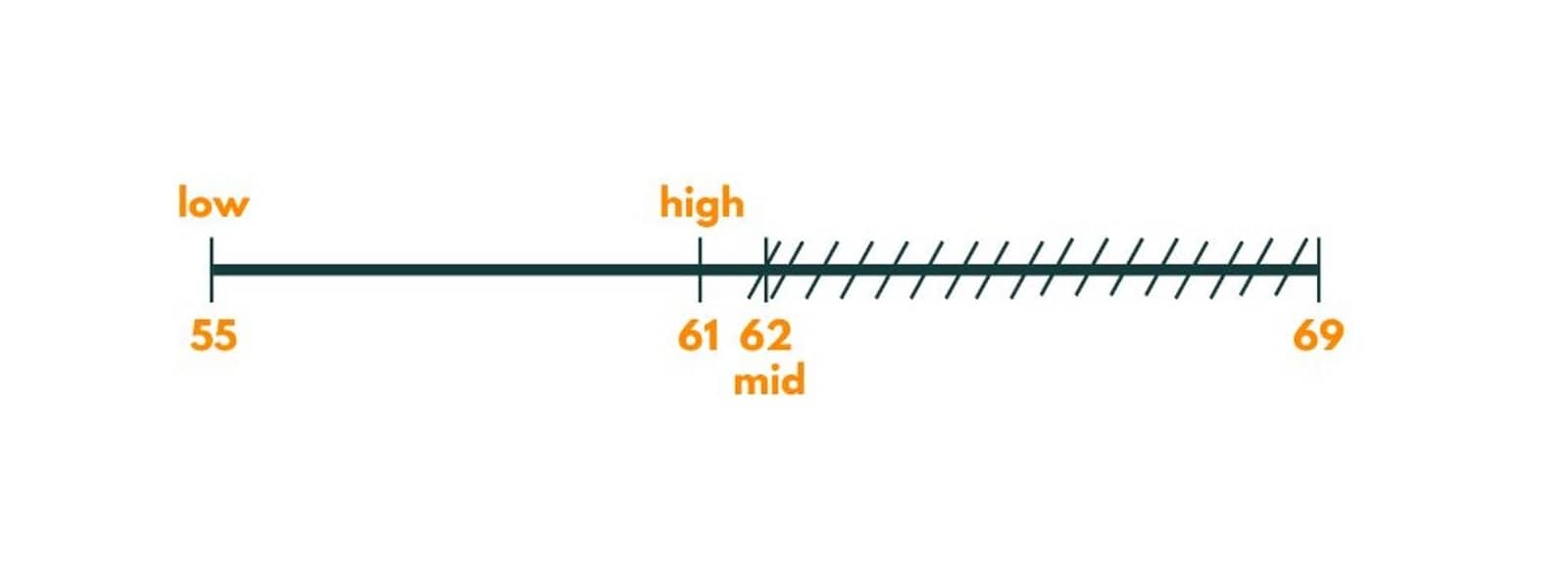
Iteration 4
Now, the mid is 58.
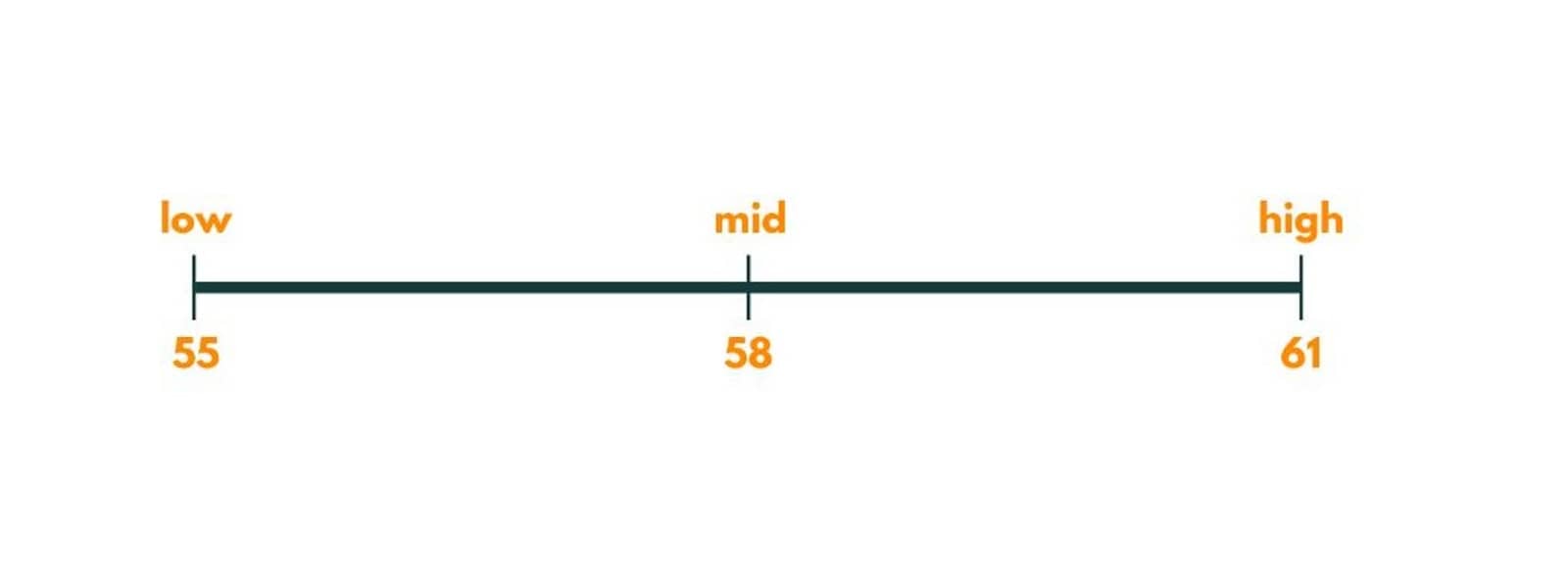
Again the painters needed would be 3. So we move right and put lo as mid + 1 i.e. 59.
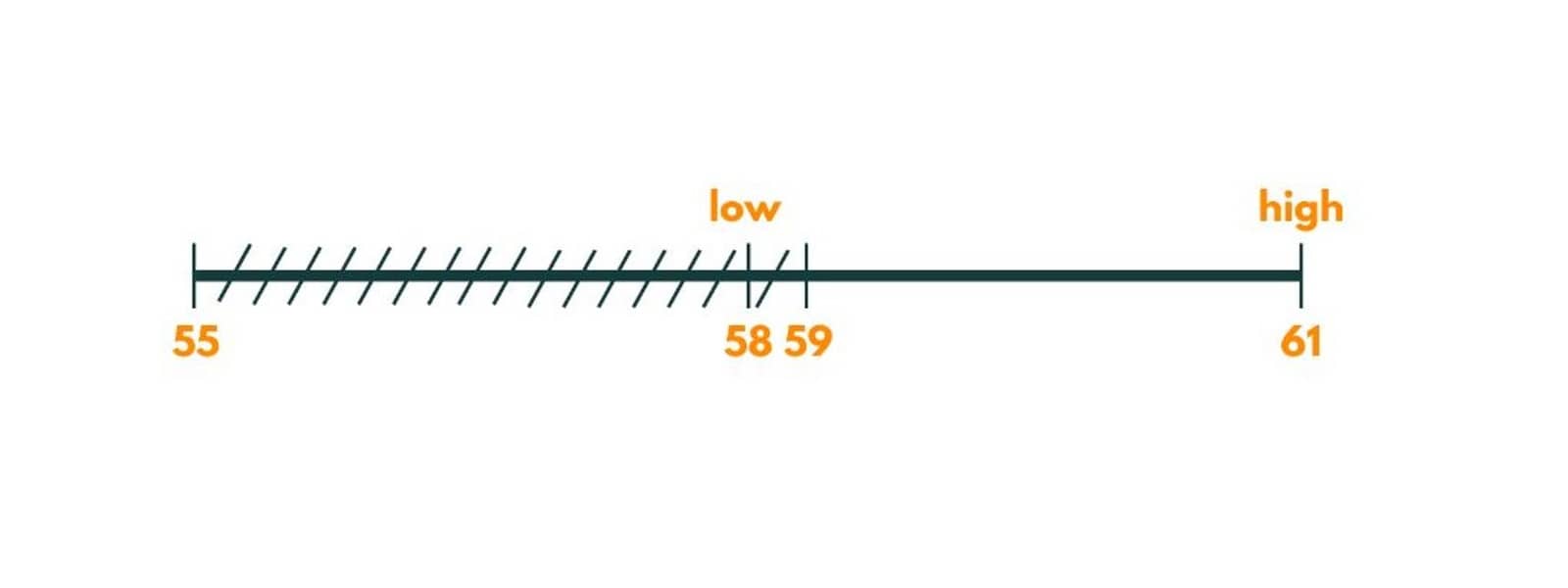
Iteration 5
Here, the mid is 60.
The painters needed would be 2 with maxTime as 6, so we store it as our potential answer and move left by putting a high as 59.
Now as low and high are pointing to the same element, we stop and the answer comes out to be 60.
Time & Space Complexity
Here, we are performing a binary search, that takes O(LogN) time for an array of size N, and for each mid we find, we are counting the painters needed by traversing over the array. So, the total time complexity comes out to be O(NLogN). Also, As no extra space has been used in the algorithm, the space complexity comes out to be O(1).
Conclusion
So the Painters Partition Problem is an important problem from an interview point of view and demands in-depth knowledge of the binary search concept. With the example above, you can easily understand it. The problem has applications in various fields, including economics and game theory.








