Kruskal's Algorithm in Java: Find Minimum Spanning Tree

Kruskal's Algorithm is an important greedy algorithm that helps you find the shortest path between 2 cities. So, before learning what Kruskal's algorithm in Java is, let's just go through the basics first.

What is a Spanning Tree?

A spanning tree is a sub-graph or a tree of the given directed and connected graph including all the vertices and minimum possible edges. And as a tree has no loops, a spanning tree also doesn't contain any cycles or loops. 

 A minimum Spanning tree is a kind of spanning tree in which the sum of the weights of edges is the minimum. A graph can have many spanning trees but can only have a unique minimum spanning tree.

Let's take an example from this graph:

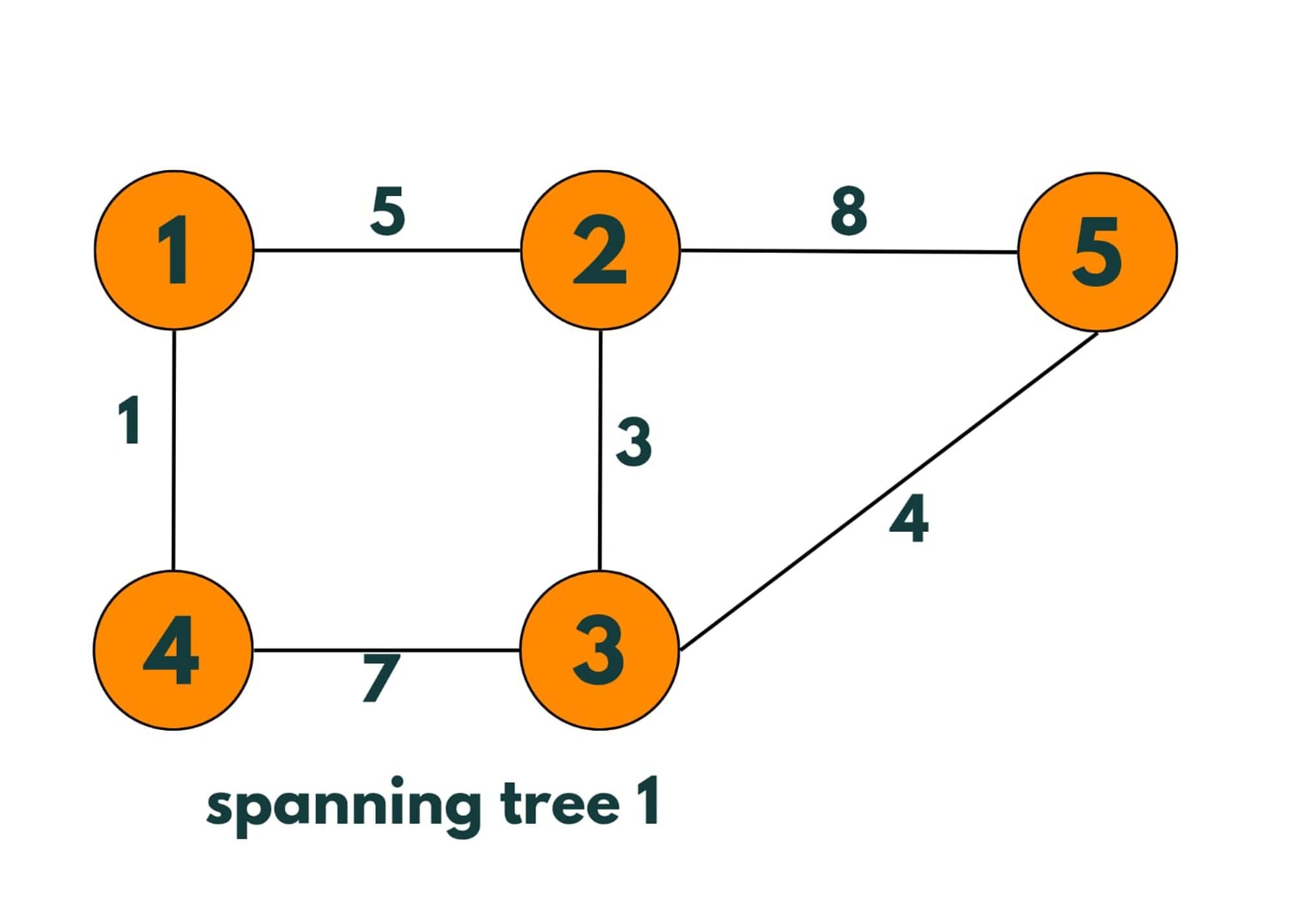
Spanning trees made from this graph:

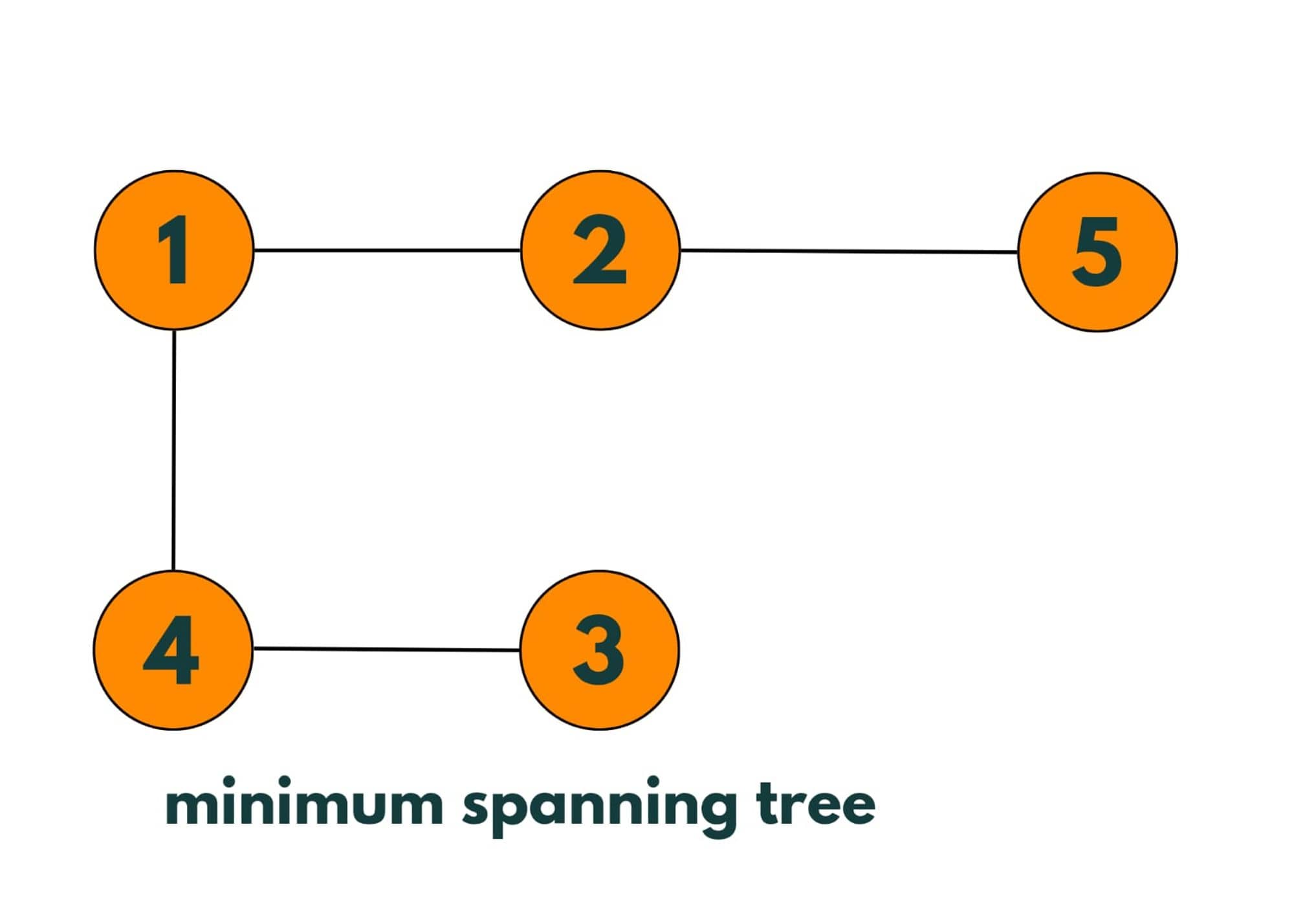
More spanning trees can be made from the given graph. The Minimum Spanning Tree will be: 

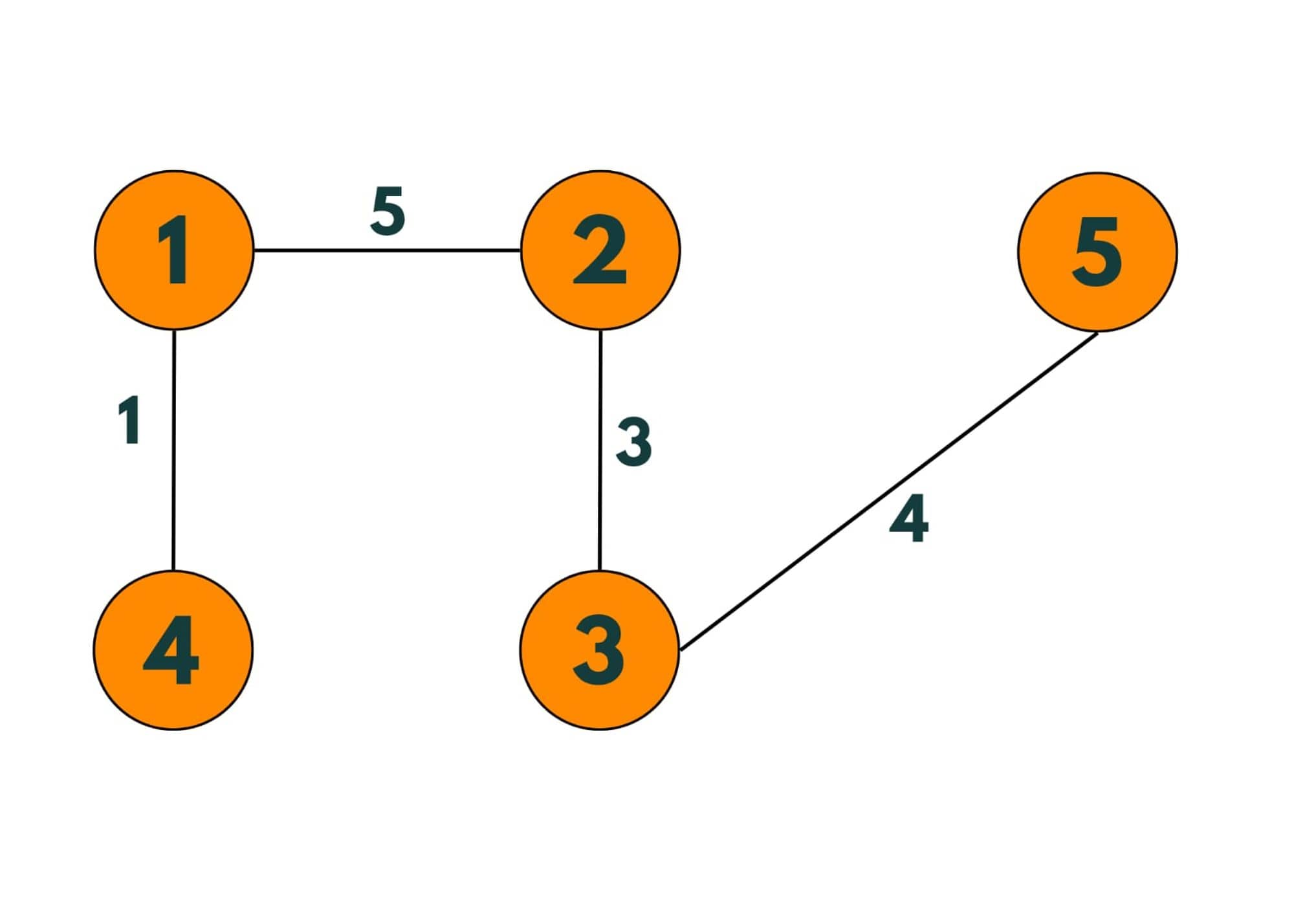
To create a minimum spanning tree from a graph, we select all vertices and a minimum number of edges connecting those vertices, so that no cycle is created and we select only those edges whose cost of edges is minimum. 

What is Kruskal's Algorithm?

Kruskal's algorithm is a realistic algorithm that provides the shorted path from one place to another in terms of edge weights or cost. This produces output exactly the same as prim's algorithm but the process or algorithm differs.

It greedily picks n-1 edges one by one from the graph that has the minimum cost such that no cycle is created. So Kruskal's Algorithm takes up a connected and undirected graph and returns its minimum spanning tree.

How does Kruskal Algorithm work?

Let's take an example of this graph:

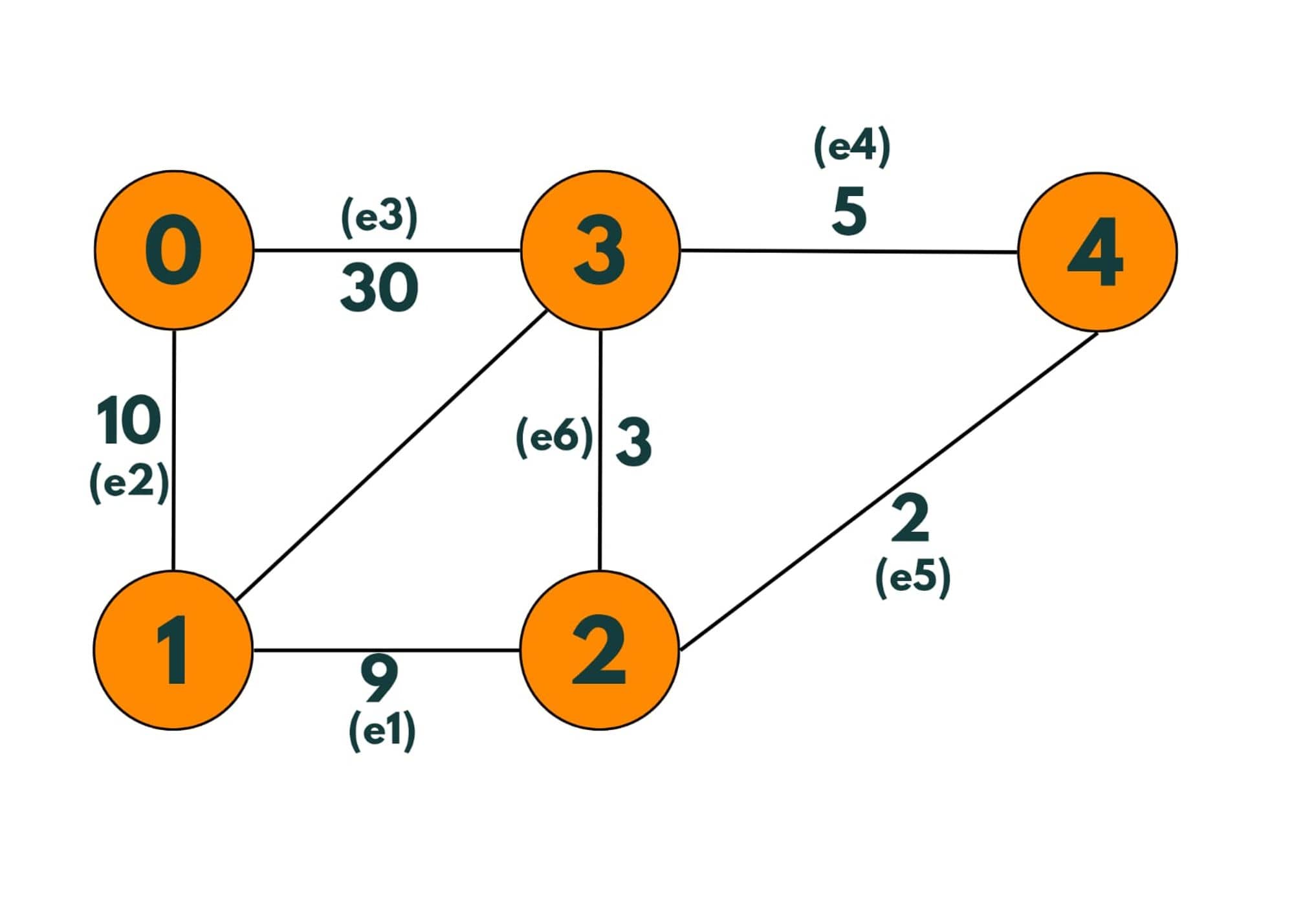
Step 1: So as the first step we take the edge having the smallest weight and add it to our minimum spanning tree.

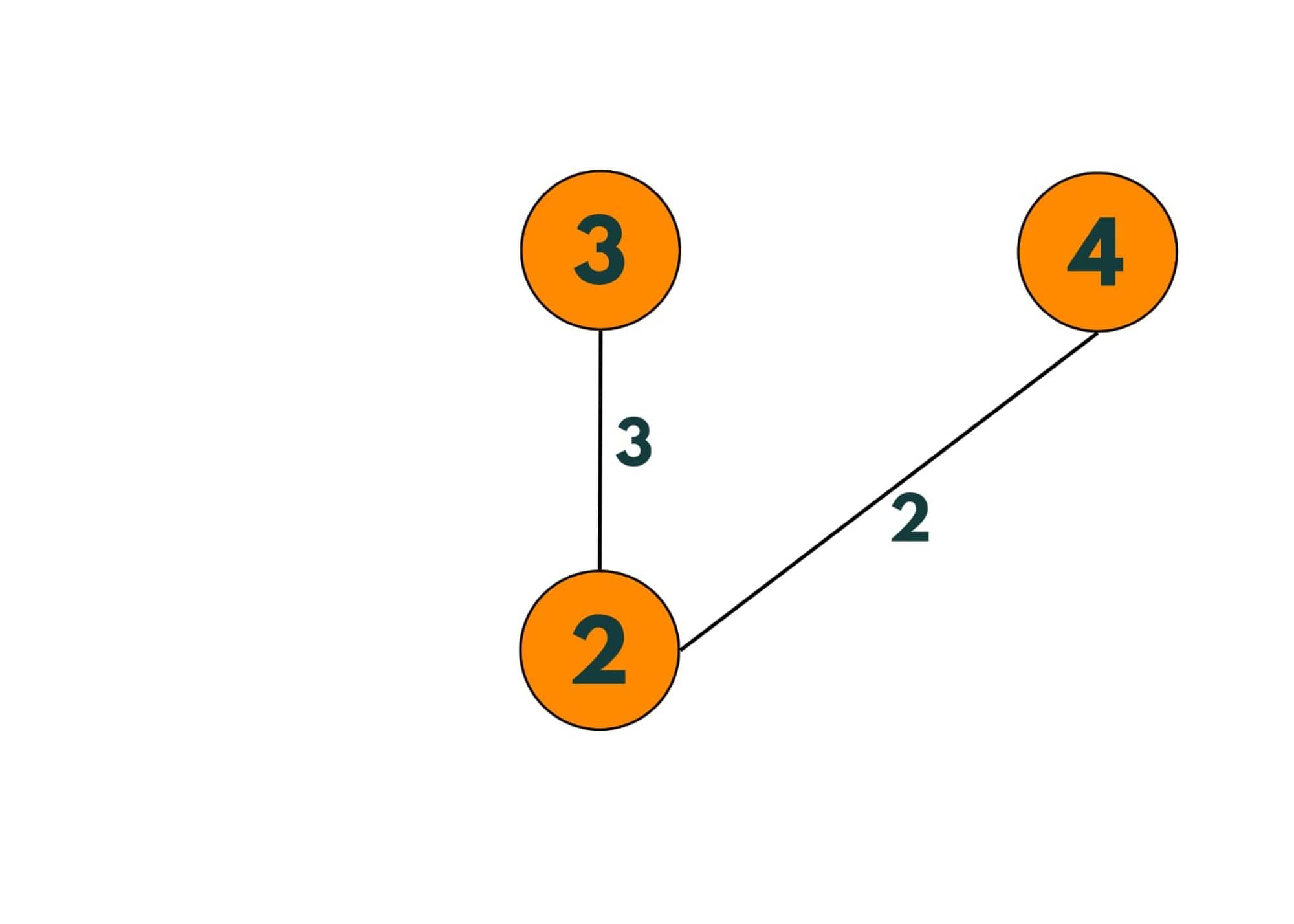
Step 2: Now we take the edge having the smallest weight among the edges that aren't added to the tree yet.  So as the edge we are going to add (e6) doesn't make a cycle, we add it to the minimum spanning tree.

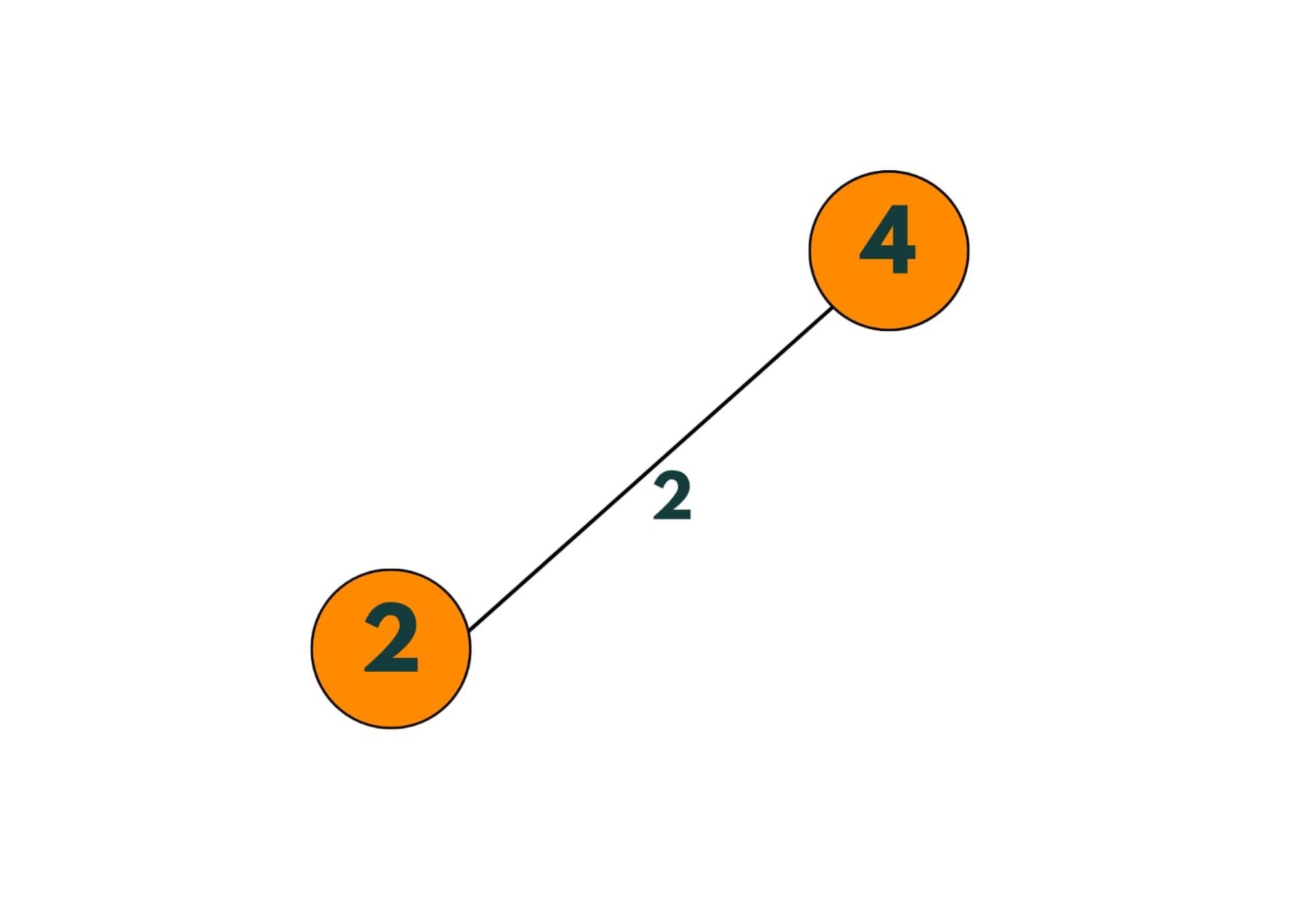
Step 3: Now the smallest weighted edge is of weight 7. But as we add that edge to the minimum spanning tree, it creates a cycle, so we skip.

Step 4: Now smallest weighted edge is e1 having weight = 9. As it doesn't create a loop, we add it to the tree.

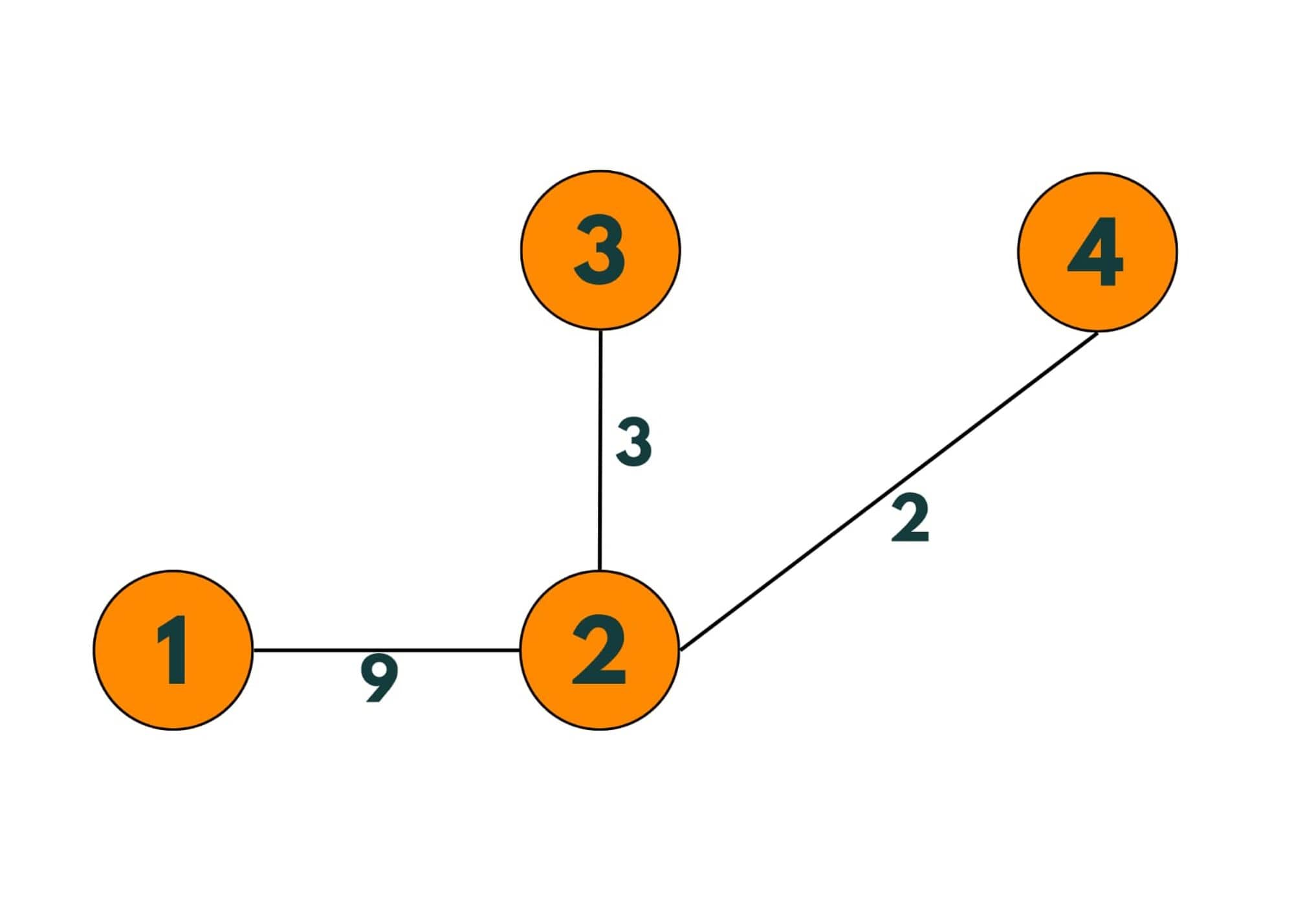
Step 5: Next smallest weighted edge is e2. So adding it to the tree.

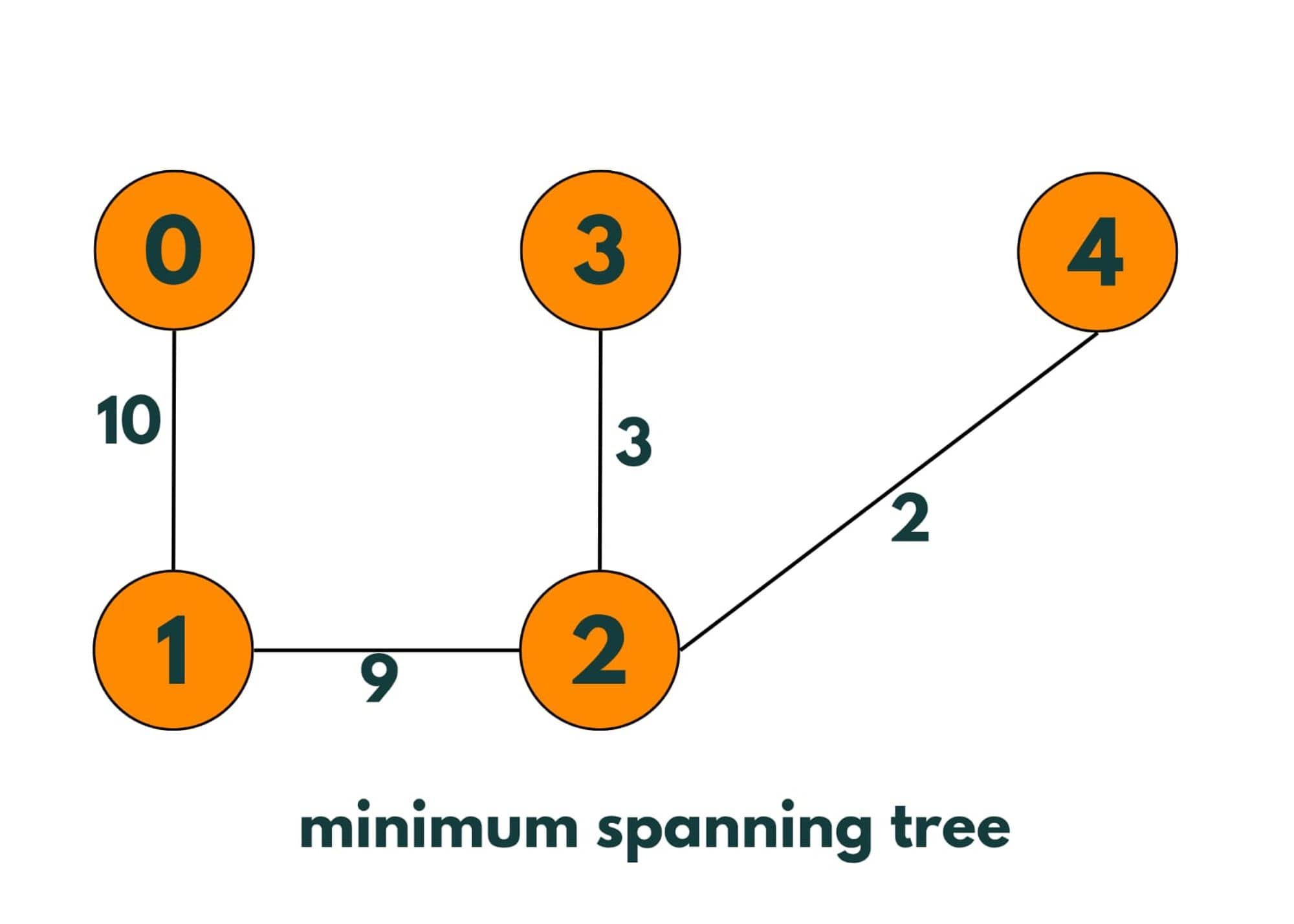
So as of now, we have added n-1 minimum weighted edges of the graph to the tree and as no cycle is there, it is a minimum spanning tree.

Here is the full algorithm:

1. We make a pair class to store the vertices and edges and put all the pairs in an array.
2. Then we sort the array so that we can access the least weighted edge.
3. Now we loop on the sorted array.
4. We check using DSU (disjoint sets and union) whether both edges belong to the same group or component or not.
5. If not we merge them, else we continue.
6. We keep doing so till we get the minimum Spanning tree with all vertices, minimum edges, and no cycles.

Kruskal Algorithm in Java

Here is the full program to implement Kruskal Algorithm in Java:

import java.util.*;

public class Kruskal {

	public static void main(String[] args) {
		
	    int[][] edges = new int[5][3];
		
	    edges[0][0] = 0;
	    edges[0][1] = 1;
	    edges[0][2] = 10;
	    
	    edges[1][0] = 1;
	    edges[1][1] = 2;
	    edges[1][2] = 9;
	    
	    edges[2][0] = 2;
	    edges[2][1] = 4;
	    edges[2][2] = 2;
	    
	    edges[3][0] = 4;
	    edges[3][1] = 3;
	    edges[3][2] = 5;

	    edges[4][0] = 3;
	    edges[4][1] = 2;
	    edges[4][2] = 3;
	    
	    int ans = KruskalAlgo(5, edges);
	    System.out.println("The min cost is");
	    System.out.println(ans);
	    
	}

	  static int[] parent;
	  static int[] rank;
	  
	  //creating a class of pair to maintain it in an array 
	  public static class Pair implements Comparable <Pair> {
		 
	    int vertex1;
	    int vertex2;
	    int weight;

	    Pair(int vertex1, int vertex2, int weight) {
	      this.vertex1 = vertex1;
	      this.vertex2 = vertex2;
	      this.weight = weight;
	    }

	    @Override
	    public int compareTo(Pair o) {
	      //comparing the edges by their weights.
	      return this.weight - o.weight;
	    }
	  }

	  public static int KruskalAlgo(int n, int[][] edge) {

            System.out.print("Minimum Spanning Tree is :-");
            System.out.println();
	    System.out.println("V1" + " V2" + " Wt");
		//1. to store the edges in sorted order.
		// array of all the edges containing pair of vertices and weight given to that edge.
	    Pair[] edges = new Pair[edge.length];
	    
	    //inserting all the  pairs of vertices and their respective weigts in 'edges'.
	    for (int i = 0; i < edges.length; i++) {
	      int vertex1 = edge[i][0];
	      int vertex2 = edge[i][1];
	      int weight = edge[i][2];
	      edges[i] = new Pair(vertex1, vertex2, weight);
	    }

	    int ans = 0;
	    Arrays.sort(edges);
	    
	    parent = new int[n + 1];
	    rank = new int[n + 1];
	    
	    // assigning each element as a unique group and assigning rank 1 to them.
	    for (int i = 0; i < parent.length; i++) {
	      parent[i] = i;
	      rank[i] = 1;
	    }

	    
	    for (int i = 0; i < edges.length; i++) {
	      int vertex1 = edges[i].vertex1;
	      int vertex2 = edges[i].vertex2;
	      int weight = edges[i].weight;
	      
	      //checking if the vertices belong to same group or not.
	      boolean flag = union(vertex1, vertex2);
	      
	      //if vertices are from unique groups that implies , if both vertices would be connected, it won't create a loop.
	      if (flag == false) {
	    	System.out.println(vertex1+"  "+vertex2+"  "+weight);
	        ans += weight;
	      }
	    }
	    
	    return ans;

	  }

	  public static int find(int component) {
		  
		// if the component which is a leader already is returned.
	    if (parent[component] == component) {
	      return component;
	    }
	    
	    //finding the parent  or group leader of that  element
	    int temp = find(parent[component]);
	    parent[component] = temp;
	    return temp;
	  }

	  public static boolean union(int vertex1, int vertex2) {
		  
		// finding the parent or group leader of both of these vertices.
	    int parentOfVertex1 = find(vertex1);
	    int parentOfVertex2 = find(vertex2);
	    
	    //if parent or leader of both vertices is same, this implies, that if they get connected, it would create a loop
	    if (parentOfVertex1 == parentOfVertex2) {
	      return true;
	    }
	    
	    //deciding the parent of vertex according to their ranks.
	    if (rank[parentOfVertex1] > rank[parentOfVertex2]) {
	      parent[parentOfVertex2] = parentOfVertex1;
	    } else if (rank[parentOfVertex1] < rank[parentOfVertex2]) {
	      parent[parentOfVertex1] = parentOfVertex2;
	    } else {
	      parent[parentOfVertex1] = parentOfVertex2;
	      rank[parentOfVertex2]++;
	    }
	    
	    return false;
	  }
}

Output:

Minimum Spanning Tree is :- 

V1 V2 Wt
2  4  2
3  2  3
1  2  9
0  1  10
The min cost is
24

Time & Space Complexity

As the first step of Kruskal's algorithm, we are sorting the edges based on their weights. Assuming that graph has E Edges, so time complexity is 3 * (E log E) as there are 3 elements - the 2 vertices and weight.

So, it's near O(E Log E). After that, we iterate over these edges and we try to find out if they belong to the same group/component or not, it's time complexity comes out to be  O(E * O(4 Alpha)). So total time complexity comes out to be (E Log E).

And as we are using an extra space of O(E) to store the sorted edges, space complexity comes out to be O(E).

Applications & Uses

Here are some practical coding use cases for Kruskal's algorithm:

• Kruskal is a popular algorithm used to find minimum-spanning trees.
• This algorithm can be used to design a cost-effective network by only connecting the vertices having edges of minimum cost.
• It can also be applied to the transportation of goods between different cities. As it is possible to find out the shortest path between warehouses that reduces the transportation time and cost.
• It is an efficient algorithm that can save money by reducing the pipes to supply water, as we can easily find out the minimum cost to supply water in a city.
• Can be used for electrical wiring too.

Conclusion

 So Kruskal's Algorithm in Java is not only important from the interview point of view but also, as it is used in the real world to solve problems where we need to find the shortest path between 2 cities or networks.  Got a question about Algorithms in programming, connect with our experts for Java homework help online anytime!