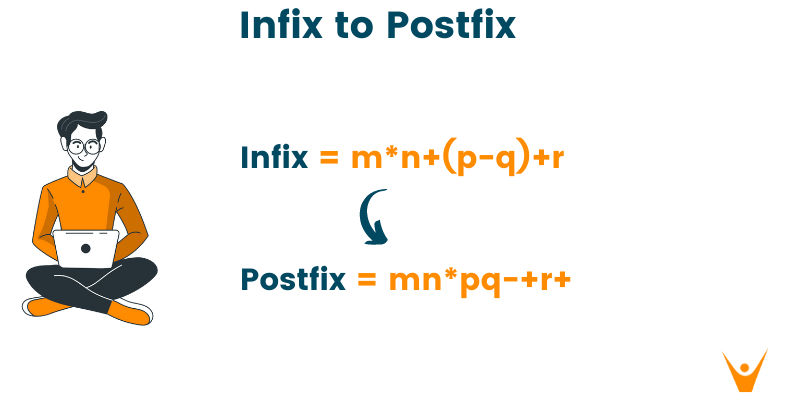Infix to Postfix Conversion (With C++, Java and Python Code)

In mathematical expressions, parentheses are often used to make their meaning easier to interpret. In computers, however, parentheses in an expression can increase the time needed to solve for a solution. To minimize computational complexity, various notations have been devised for representing operators and operands in an expression.

In this article, let us study a couple of those notations, namely, infix and postfix notation, in detail, along with its example. We will also dive deep to understand the technique for converting infix to postfix notation along with c++, java, and python code implementation. So, let’s get started!

What is Infix Notation?

When the operator is placed between its operands, it is known as infix notation. The operand is not necessarily a constant or a variable—it can also be an expression.

For example: (a + b) * (c + d)

The above expression contains three operators. The operands for the first plus operator are a and b, whereas the operands for the second plus operator are c and d. Evaluating the result of these operations requires applying some set of rules. At last, after using the addition operator on (a + b) and (c + d), the multiplication operation will be performed to look towards the final answer. 

Syntax:

<operand> <operator> <operand> 

Remember that if there is only one operator in the expression, we do not have to follow any rule set to evaluate the expression. However, if the expression possesses more than one set of operators, you can define the operator's priority according to the below-given table and evaluate the final result. 

What is Postfix Notation?

The expression in which the operator is written after the operands is known as postfix expression or reverse polish notation. 

For example, the postfix notation of infix expression (a + b) can be written as ab+. 

Postfix expression is an arithmetic expression in which operators are applied from left to right. There is no need for parentheses while working with postfix notation, unlike infix expressions. Moreover, no operator precedence rules or associativity rules are needed, meaning that coders do not need to memorize a special set of rules to help them determine the order in which operations will be performed.

Let us understand the algorithm to define postfix notation using an example

Algorithm for postfix notation

Let the infix notation of an expression be: a  + b * c

Here, we will start scanning the expression from the left side. As the multiplication operator is the first operator appearing while scanning expression from left to right, the expression will be 

Resultant Expression 1: a + bc*

Again, we scan the expression from left to right, and the next operator encountered will be plus. As a result, the final output of the expression will be

Resultant Expression 2: abc+*

Therefore, the final algorithmic steps for the postfix expression are:

1) Scanning the expression from left to right
2) If the operand is encountered, push it into the stack
3) If the operator is encountered, then pop the corresponding operand from the stack and perform computation
4) Continue the same process and retain the final value in the stack

How to Convert Infix to Postfix Expression?

Using the stack data structure is the best method for converting an infix expression to a postfix expression. It holds operators until both operands have been processed, and it reverses the order of operators in the postfix expression to match the order of operation.

Here is an algorithm that returns the string in postfix order, left to right. For each token, there are four cases:

1. If the current token is an opening parenthesis, push it into the stack.
2. If the current token is a closing parenthesis, pop tokens from the stack until a corresponding opening parenthesis are popped. Append each operator to the end of the postfix expression.
3. Append the current token to the end of the postfix expression if it is an operand
4. If the current token is an operator, append it to the postfix expression with higher precedence than the operator on top of the stack. If it has lower precedence, first pop operators from the stack until we have a higher precedence operator on top, or the stack becomes empty.
5. Finally, if you have any remaining operators in the stack, add them to the end of the postfix expression until the stack is empty and return the postfixed expression.

Let us understand the conversion of infix to postfix notation using stack with the help of the below example

Example

Let the expression to be evaluated be m*n+(p-q)+r

Therefore, the final output as postfix notation for the above expression is mn*pq-+r+

Python Code for Infix to Postfix Conversion

Operators = set(['+', '-', '*', '/', '(', ')', '^'])  # collection of Operators

Priority = {'+':1, '-':1, '*':2, '/':2, '^':3} # dictionary having priorities of Operators
 
 
def infixToPostfix(expression): 

    stack = [] # initialization of empty stack

    output = '' 

    

    for character in expression:

        if character not in Operators:  # if an operand append in postfix expression

            output+= character

        elif character=='(':  # else Operators push onto stack

            stack.append('(')

        elif character==')':

            while stack and stack[-1]!= '(':

                output+=stack.pop()

            stack.pop()

        else: 

            while stack and stack[-1]!='(' and Priority[character]<=Priority[stack[-1]]:

                output+=stack.pop()

            stack.append(character)

    while stack:

        output+=stack.pop()

    return output


expression = input('Enter infix expression ')

print('infix notation: ',expression)

print('postfix notation: ',infixToPostfix(expression))

Output

Enter infix expression m*n+(p-q)+r
infix notation:  m*n+(p-q)+r
postfix notation:  mn*pq-+r+

Java Code for Infix to Postfix Conversion

import java.io.*;
import java.lang.reflect.Array;
import java.util.*;
import java.lang.*;
public class favtutor{

    public static int precedence(char x){

        if(x=='^'){   // highest precedence
            return 2;
        }
        else if(x=='*' || x=='/'){
            return 1;                        // second highest precedence
        }
        else if(x=='+' || x=='-'){
            // lowest precedence

            return 0;
        }
        return -1; // not an operator
    }

    public static String InfixToPostfix(String str){

        Stack<Character>stk= new Stack<>();             // used for converting infix to postfix

        String ans="";                // string containing our final answer

        int n= str.length();

        for (int i = 0; i <n ; i++) {
            char x= str.charAt(i);

            if(x>='0' && x<='9'){
                ans+=x;
            }

            else if(x=='('){     // push directly in the stack
                stk.push('(');
            }
            else if(x==')'){

                while(!stk.isEmpty() && stk.peek()!='('){          // keep popping till opening bracket is found
                    ans+=stk.pop();
                }
                if(!stk.isEmpty()){
                    stk.pop();
                }

            }
            else{

                while(!stk.isEmpty() && precedence(stk.peek())>=precedence(x)){    // remove all higher precedence values
                    ans+=stk.pop();
                }
                stk.push(x);

            }
        }
        while(!stk.isEmpty()){
            ans+=stk.pop();
        }
        return ans;
    }
}

Output

m*n+(p-q)+r
mn*pq-+r+

C++ Code for Infix to Postfix Conversion

#include<bits/stdc++.h>
using namespace std;

// A Function to return precedence of operators
int prec(char ch) {
	if (ch == '^')
		return 3;
	else if (ch == '/' || ch == '*')
		return 2;
	else if (ch == '+' || ch == '-')
		return 1;
	else
		return -1;
}

// A Function to convert infix expression to postfix expression
string infixToPostfix(string s) {

	stack<char> st; //For stack operations, we are using C++ built in stack
	string ans = "";

	for (int i = 0; i < s.length(); i++) {
		char ch = s[i];

		// If the current character is an operand, add it to our answer string.
		if ((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z') || (ch >= '0' && ch <= '9'))
			ans += ch;   // Append the current character of string in our answer

		// If the current character of string is an '(', push it to the stack.
		else if (ch == '(')
			st.push('(');

		// If the current character of string is an ')', append the top character of stack in our answer string
		// and pop that top character from the stack until an '(' is encountered.
		else if (ch == ')') {
			while (st.top() != '(')
			{
				ans += st.top();    // Append the top character of stack in our answer
				st.pop();
			}
			st.pop();
		}

		//If an operator is scanned
		else {
			while (!st.empty() && prec(s[i]) <= prec(st.top())) {
				ans += st.top();
				st.pop();
			}
			st.push(ch);             // Push the current character of string in stack
		}
	}

	// Pop all the remaining elements from the stack
	while (!st.empty()) {
		ans += st.top();
		st.pop();
	}

	return ans;
}

int main() {
	string s;
	cin >> s;
	cout << infixToPostfix(s);
	return 0;
}

Output

m*n+(p-q)+r
mn*pq-+r+

Time Complexity

The time complexity of the above solution to convert infix to postfix notation is O(n), where n is the length of infix expression. Similarly, the space complexity for the conversion is O(n) as it requires equal space to execute the solution using the stack data structure. 

Conclusion

Infix expressions are what we humans use to solve problems normally. However, computers require a stack to solve expressions. Without taking care of the operator’s precedence, it is easy for the systems to solve the expressions using prefix and postfix notation. In this article, we studied a detailed view of infix and postfix notation along with the simplest technique to convert infix to postfix notation using the stack data structure. It is highly recommended to understand this problem thoroughly to make your programming easy and efficient.