Huffman coding is a type of greedy algorithm developed by David A. Huffman during the late 19th century. It is one of the most used algorithms for various purposes all over the technical domain. In this article, we will study Huffman coding, example, algorithm, and its implementation using python.
What is Huffman Coding?
Huffman coding is a greedy algorithm frequently used for lossless data compression. The basic principle of Huffman coding is to compress and encode the text or the data depending on the frequency of the characters in the text.
The idea of this algorithm is to assign variable-length codes to input characters of text based on the frequencies of the corresponding character. So, the most frequent character gets the smallest code, and the least frequent character is assigned the largest code.
Here, the codes assigned to the characters are termed prefix codes which means that the code assigned to one character is not the prefix of the code assigned to any other character. Using this technique, Huffman coding ensures that there is no ambiguity when decoding the generated bitstream.
Is Huffman coding a Greedy algorithm?
Yes, Huffman coding is a greedy algorithm. It works by selecting the lowest two frequency symbols/subtrees and merging them together at every step until all symbols or subtrees are merged into a single binary tree. This method ensures that the final binary tree minimizes the total number of bits required to represent the symbols in the input.
As a result, Huffman coding is regarded as a classic example of a greedy algorithm.
Huffman Coding Example
Let us understand how Huffman coding works with the example below:
Consider the following input text:

As the above text is of 11 characters, each character requires 8 bits. Therefore, a total of 11x8=88 bits are required to send this input text.
Using Huffman coding, we will compress the text to a smaller size by creating a Huffman coding tree using the character frequencies and generating the code for each character.
Remember that we encode the text while sending it, and later, it is necessary to decode it. Hence, the decoding of the text is done using the same tree generated by the Huffman technique.
Let us see how to encode the above text using the Huffman coding algorithm:
Looking at the text, the frequencies of the characters will be as shown in the below image.

Now, we will sort the frequencies string of the characters in increasing order. Consider these characters are stored in the priority queue as shown in the below image.
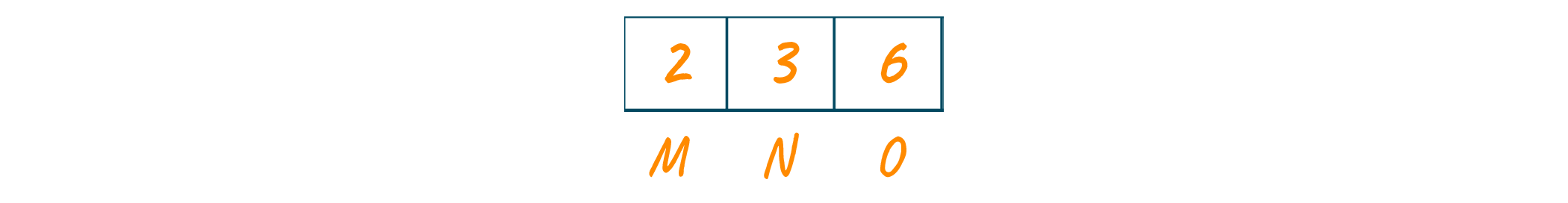
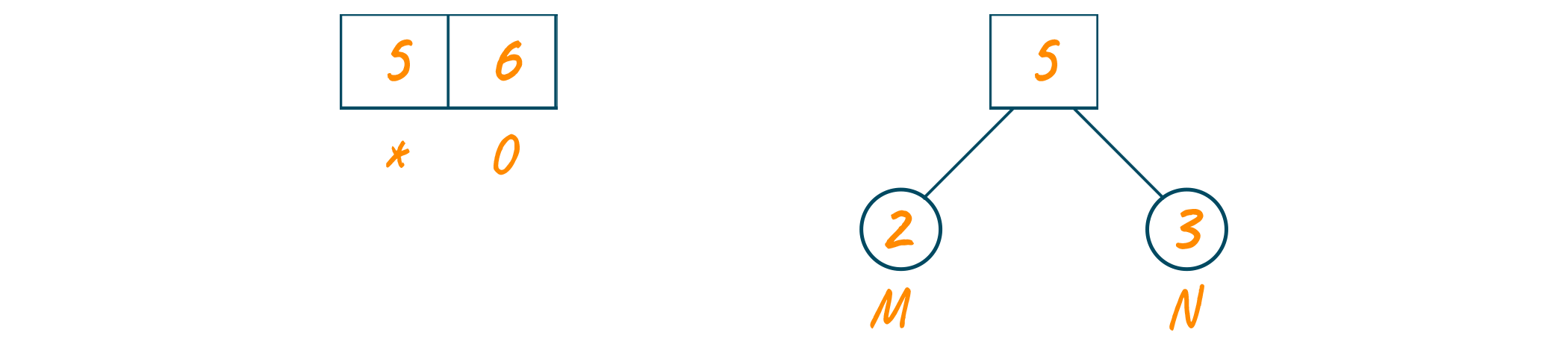
Now, we will create the Huffman tree using this priority queue. Here, we will create an empty node ‘a’. Later, we will assign the minimum frequency of the queue as the left child of node ‘a’ and the second minimum frequency as the right child of node ‘a’.
The value of node ‘a’ will be the sum of both minimum frequencies and add it to the priority queue as shown in the below image.
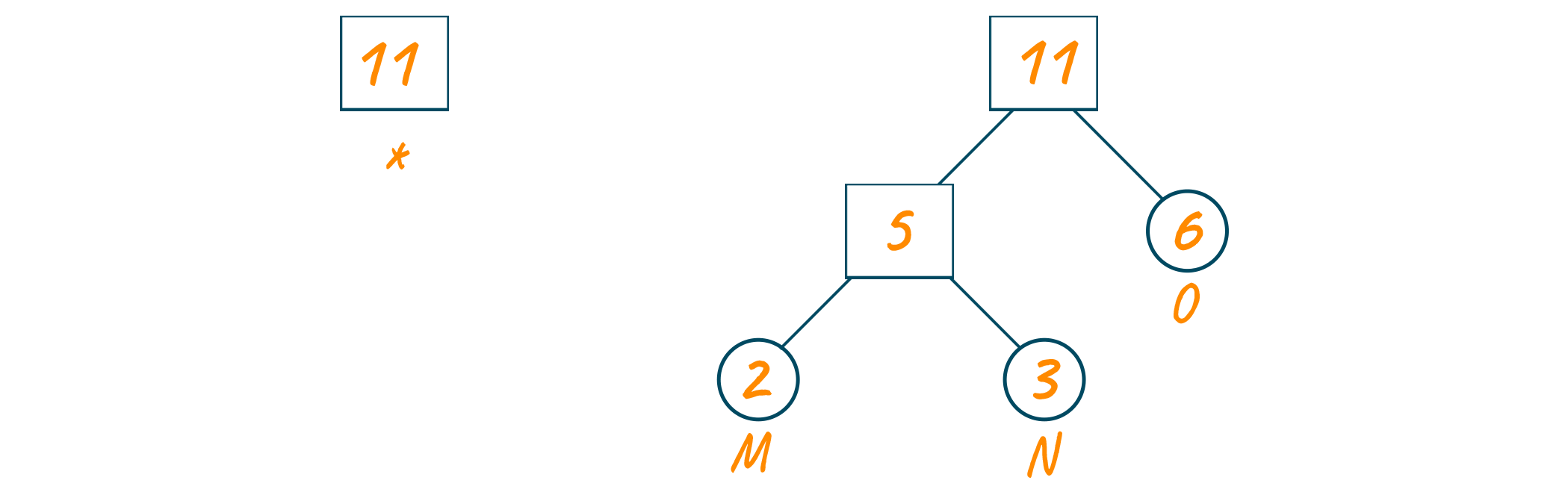
Repeat the same process until the complete Huffman tree is formed.
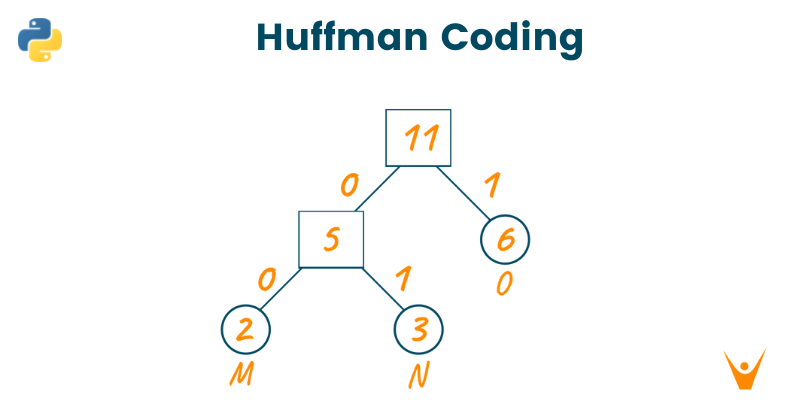
Now, assign 0 to the left edges and 1 to the right edges of the Huffman coding tree as shown below.
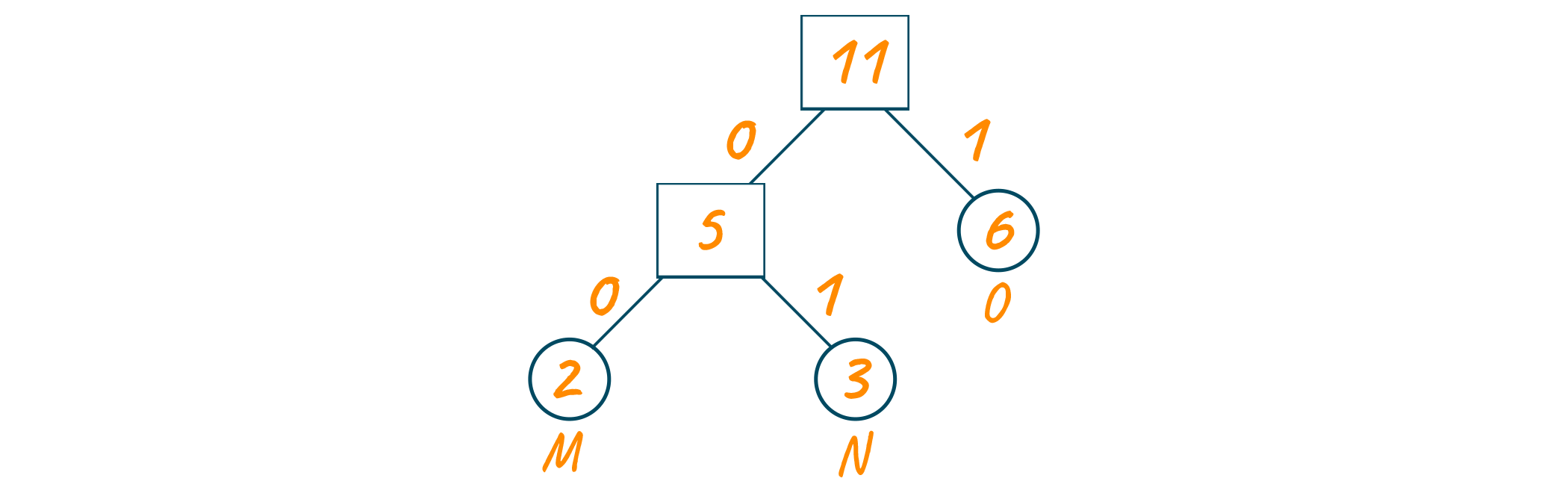
Remember that for sending the above text, we will send the tree along with the compressed code for easy decoding. Therefore, the total size is given in the table below:
|
Character |
Frequency |
Code |
Size |
|
M |
2 |
00 |
2*2 = 4 |
|
N |
3 |
01 |
3*2 = 6 |
|
O |
6 |
1 |
6*1 = 6 |
|
3*8 = 24 bits |
11 bits |
|
16 bits |
Without using the Huffman coding algorithm, the size of the text was 88 bits. Whereas after encoding the text, the size is reduced to 24 + 11 + 16 = 51 bits.
How to decode the code?
For decoding the above code, you can traverse the given Huffman tree and find the characters according to the code. For example, if you wish to decode 01, we traverse from the root node as shown in the below image.
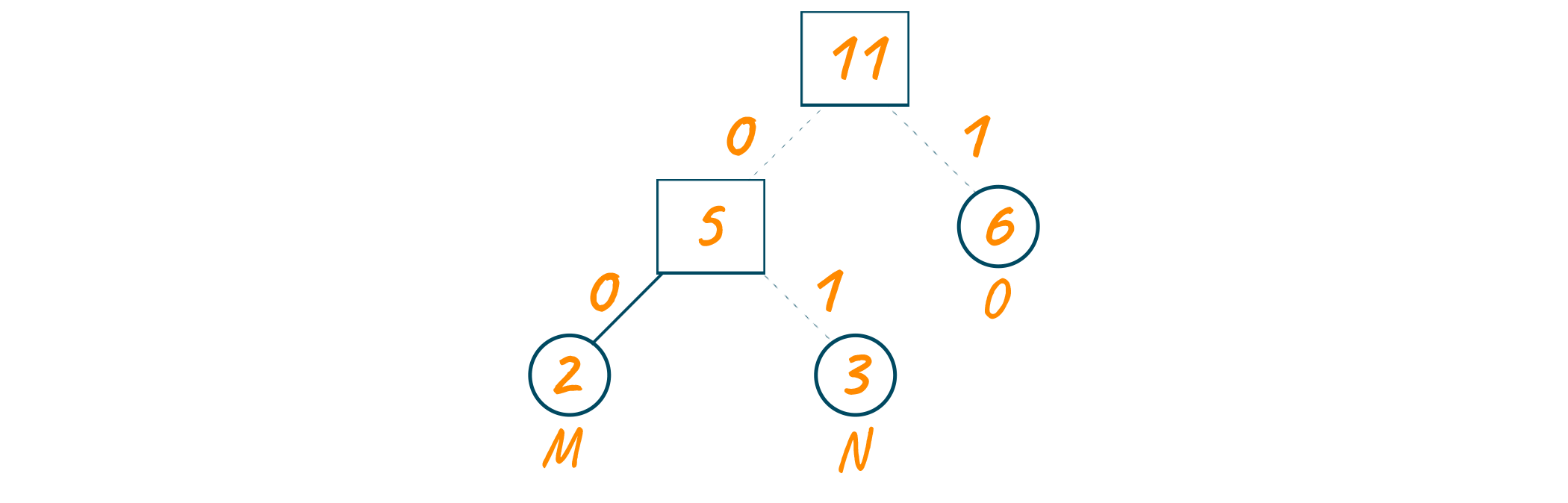
Algorithm for Huffman Coding
Here is the complete algorithm for huffman coding:
1. initiate a priority queue 'Q' consisting of unique characters. 2. sort the priority queue according to the ascending order of frequencies 3. for all the unique characters inside the queue: Initialize a new Node 'a' Return the minimum value of Q and assign it to the left child of 'a' Return the next minimum value of Q and assign it to the right Child of 'a' find the sum of both returned values and assign it as the value of 'a' insert the value of 'a' into the tree 4. repeat the same process until all unique characters of 'Q' are visited 5. Return root node
Implementation using Python
Here is the full code to implement Huffman coding in Python:
from collections import Counter class NodeTree(object): def __init__(self, left=None, right=None): self.left = left self.right = right def children(self): return self.left, self.right def __str__(self): return self.left, self.right def huffman_code_tree(node, binString=''): ''' Function to find Huffman Code ''' if type(node) is str: return {node: binString} (l, r) = node.children() d = dict() d.update(huffman_code_tree(l, binString + '0')) d.update(huffman_code_tree(r, binString + '1')) return d def make_tree(nodes): ''' Function to make tree :param nodes: Nodes :return: Root of the tree ''' while len(nodes) > 1: (key1, c1) = nodes[-1] (key2, c2) = nodes[-2] nodes = nodes[:-2] node = NodeTree(key1, key2) nodes.append((node, c1 + c2)) nodes = sorted(nodes, key=lambda x: x[1], reverse=True) return nodes[0][0] if __name__ == '__main__': string = 'BCAADDDCCACACAC' freq = dict(Counter(string)) freq = sorted(freq.items(), key=lambda x: x[1], reverse=True) node = make_tree(freq) encoding = huffman_code_tree(node) for i in encoding: print(f'{i} : {encoding[i]}')
Time Complexity
The time complexity of Huffman coding is O(n logn), where n is the number of unique characters. It is because the encoding of the text is dependent on the frequency of the characters.
What are the two types of encodings in Huffman coding?
In Huffman coding, there are two types of encodings:
- Fixed-length encoding: Each symbol, irrespective of frequency, is assigned a fixed number of bits in this type of encoding. This method is not ideal for data compression and is rarely used.
- Variable-length encoding: This type of encoding assigns a variable number of bits to each symbol based on its frequency in the input. Shorter codes are assigned to more frequent symbols, while longer codes are assigned to less frequent symbols. This method is ideal for data compression and is widely used.
What is Huffman coding used for?
Here are some of the practical use cases of this algorithm:
- Huffman coding is used for conventional compression formats like GZIP, etc
- It is used for text and fax transmission
- It is used in statistical coding
- Huffman coding is used by multimedia codecs like JPEG, PNG, MP3, etc
Are there any drawbacks?
The major disadvantage of Huffman coding is that it requires two passes over the input data to build the Huffman tree, which can make it slower than other compression algorithms that only require one pass. Furthermore, in some cases, the compression achieved by Huffman coding may not be as good as that achieved by other compression algorithms.
Conclusion
Huffman coding is one of the greedy algorithms widely used by programmers all over the world. It is one of the best ways to compress the data lose it and transfer data over the network efficiently. It is highly recommended to understand the working of Huffman coding and use it to compress your data efficiently.