Hamiltonian Cycle: How to Find Hamiltonian Cycle in a Graph?

In the realm of graph theory, the Hamiltonian cycle stands as a fascinating concept that captivates mathematicians and computer scientists. Let's embark on a journey to understand the properties of Hamiltonian cycles and how to detect them.

What is a Hamiltonian Cycle?

A Hamiltonian cycle is a path in a graph that traverses all vertices exactly once and ends at the starting vertex, forming a closed loop. It is a special case of a Hamiltonian path. Both concepts play a crucial role in graph theory and have practical applications in various fields.

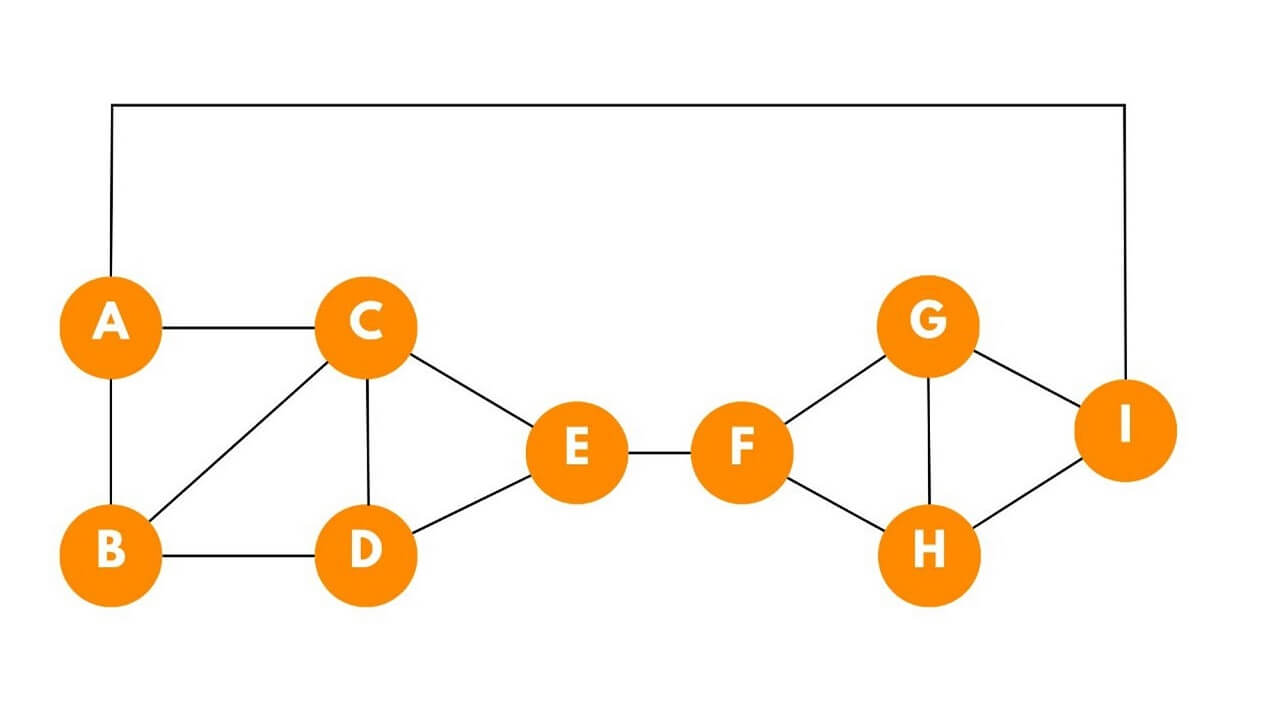
The Hamiltonian path here is A-B-C-D-E-F-G-H-I-A.

It is named after the mathematician William Rowan Hamilton. Finding Hamiltonian Cycles in graphs is an interesting task that is asked in many technical interviews. In computer science, the Traveling Salesman Problem is related to finding the shortest Hamiltonian Cycle in a complete graph where the edges have associated costs. 

It is also heavily used in finding and optimizing network routing algorithms. By ensuring that all nodes are visited efficiently, the cycles help minimize the overall distance traveled and enhance the performance of routing protocols.

Now, we get to what we are going to solve. Here is the problem statement: "Given a graph and a source, we need to find out if the Hamiltonian cycle exists in that graph or not. It exists, we need to print that path."

How to Find a Hamiltonian Cycle?

Here is the step-by-step algorithm to determine a Hamiltonian cycle in a graph:

1. We create a recursive function, say, hamiltonian, that takes the source vertex(from where we need to start), the graph, and the HashSet (that would contain all the vertices as) visited and a string called path that would contain the vertices in the hamiltonian cycle and the original source.
2. Then we first put the source in our HashSet.
3. Then we loop over the neighbors of the source.
4. If any unvisited neighbor exists, we add the source vertex to the path and call the recursive function with this unvisited neighbor as the source.
5. Now in the post area of the recursion calls to neighbors, we unvisit that neighbor, i.e., we remove it from hashSet.
6. The base case would be - If all the vertices are visited, we check if the neighbors of the current source have original source as their neighbor or not. And we return the same.

To implement it practically, we have the code in Java language below:

package Graphs;
import java.io.*;

import java.util.*;

public class hamiltonianCycle {
  static class Edge {
    int src;
    int nbr;
    int wt;

    Edge(int src, int nbr, int wt) {
      this.src = src;
      this.nbr = nbr;
      this.wt = wt;
    }
  }

  public static void main(String[] args) throws Exception {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    int vtces = Integer.parseInt(br.readLine());
    ArrayList< Edge>[] graph = new ArrayList[vtces];
    for (int i = 0; i < vtces; i++) {
      graph[i] = new ArrayList< >();
    }

    int edges = Integer.parseInt(br.readLine());
    for (int i = 0; i < edges; i++) {
      String[] parts = br.readLine().split(" ");
      int v1 = Integer.parseInt(parts[0]);
      int v2 = Integer.parseInt(parts[1]);
      int wt = Integer.parseInt(parts[2]);
      graph[v1].add(new Edge(v1, v2, wt));
      graph[v2].add(new Edge(v2, v1, wt));
    }

    int src = Integer.parseInt(br.readLine());
    

    HashSet< Integer> visited = new HashSet< >();
    hamiltonianCycleExists(graph, src, src, visited, src + "");
  }
  
  

  public static void hamiltonianCycleExists(ArrayList< Edge>[] graph, int osrc, int src, HashSet< Integer> visited, String psf) {
	  
	  //if out hashset has all the vertices 
	  if (visited.size() == graph.length - 1) {
      

      boolean closingEdge = false;
      for (Edge e : graph[osrc]) {
        if (e.nbr == src) {
          closingEdge = true;
          break;
        }
      }

      if (closingEdge) {
        System.out.println("Hamiltonian Cycle doesn't exist");
      } else {
        System.out.println("Hamiltonian Cycle Exists :");
        System.out.println(psf);
      }
      return;
    }

    visited.add(src);
    for (Edge e : graph[src]) {
      if (!visited.contains(e.nbr)) {
        hamiltonianCycleExists(graph, osrc, e.nbr, visited, psf + e.nbr);
      }
    }
    visited.remove(src);
  }
}

Output:

Hamiltonian Cycle Exists :
0125643
0346521

The time complexity depends on the structure of the graph and the existence of a Hamiltonian cycle. In the worst case, where every vertex is connected to every other vertex, the time complexity can be exponential, O(N!), where N is the number of vertices. This is because the algorithm explores all possible permutations of vertices to find a cycle.

The space complexity of the code is O(V + E) due to the graph representation and the visited set.

Conclusion

While finding a Hamiltonian cycle in an arbitrary graph remains computationally demanding, their existence and properties have profound implications in various fields. By delving deeper into Hamiltonian cycles, we continue to unravel the applications of graph theory.