Chocolate Distribution Problem & Solution (with code)

The chocolate distribution problem is a classical algorithmic problem in programming. It can be used to solve problems in the education and healthcare sectors. We will discuss this interesting problem and how to solve it using C++. So, let's get started!

What is Chocolate Distribution Problem?

Chocolate Distribution Problem statement is an array of n integers, where each integer represents the number of chocolates in a packet. The task is to distribute these chocolates among m children such that each child receives exactly one packet, and the difference between the maximum and minimum number of chocolates received by any child is minimized.

Basically, it involves distributing a given number of chocolates among a given number of children in the fairest possible way. Here is an example of it:

The chocolate distribution problem can have multiple solutions. This is because there may be multiple ways to distribute the chocolates among the children such that each child receives exactly one packet and the difference between the maximum and minimum number of chocolates received by any child is minimized.

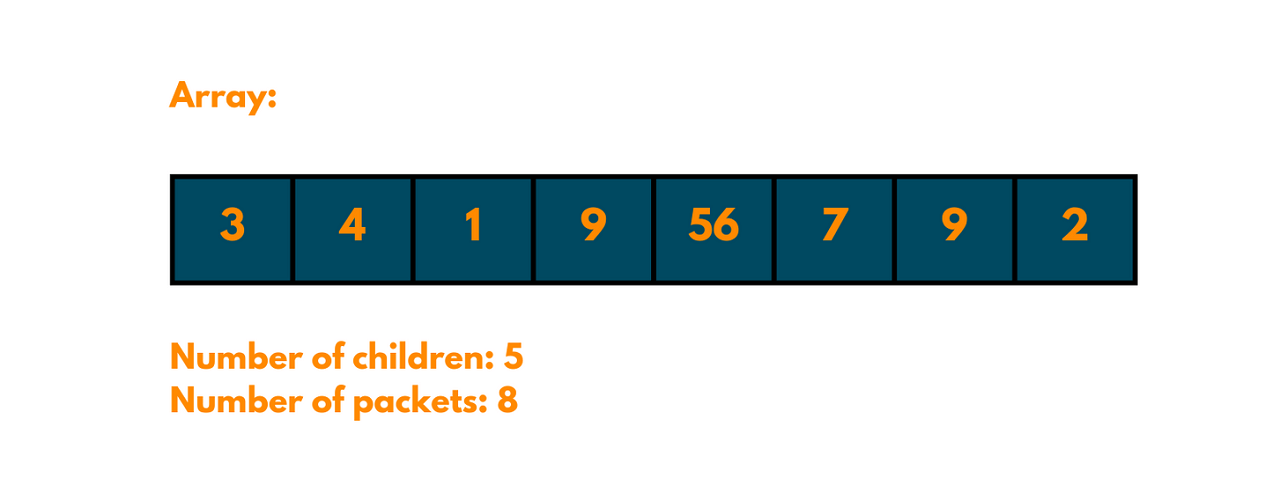
For example, consider an array [3, 4, 1, 9, 56, 7, 9, 12] and 5 children. One possible way to distribute the chocolates would be to give the first child the packet with 3 chocolates, the second child the packet with 4 chocolates, the third child the packet with 7 chocolates, the fourth child the packet with 9 chocolates, and the fifth child the packets with 9 chocolates.

The difference between the greatest and least amount of chocolates obtained by each youngster is 6, which is the smallest difference, in this manner, each child receives precisely one package.

However, there are other ways to distribute the chocolates that also give a minimum difference of 8. For example, we could give the first child the packet with 1 chocolate, the second child the packet with 3 chocolates, the third child the packet with 4 chocolates, the fourth child the packet with 9 chocolates, and the fifth child the packets with 7 chocolates. This gives a minimum difference of 8.

The problem can be solved using a greedy algorithm, which involves sorting the array in non-decreasing order and then iterating over the array to distribute the chocolates one by one to each child in a round-robin fashion.

The difference between the greatest and least amount of chocolates obtained by each youngster is 6, which is the smallest difference, in this manner, each child receives precisely one package.

The chocolate distribution problem algorithm can be used to divide resources such as textbooks, learning materials, or scholarships among students based on their academic performance. In healthcare settings, the problem algorithm can be used to allocate medical resources such as vaccines or medications among patients based on their health status or risk factors.

How to Solve the Chocolate Distribution Problem?

Here's a high-level algorithm for the chocolate distribution problem:

1. Sort the given array of chocolate packets in non-decreasing order.
2. Initialize two pointers, one at the beginning of the array and another at the (m-1)th element, where m is the number of children.
3. Compute the minimum difference between the maximum and minimum number of chocolates distributed to any child.
4. Move the pointers to the right in such a way that the minimum difference computed in step 3 is minimized.
5. Repeat steps 3 and step 4 until we have covered all possible solutions.
6. Return the minimum difference computed in step 3.

 Let's take a look at the pseudocode devised from the above algorithm:

chocolateDistribution(arr, m):
  n = length(arr)
  if m > n:
    return -1  // Invalid input

  // Step 1: Sort the array in non-decreasing order
  sort(arr, arr + n)

  // Step 2: Initialize two pointers
  start = 0
  end = m-1

  // Step 3: Compute the minimum difference
  min_diff = arr[end] - arr[start]

  // Step 4: Move the pointers to minimize the minimum difference
  for i from 1 to n-m:
    start = i
    end = i+m-1
    diff = arr[end] - arr[start]
    if diff < min_diff:
      min_diff = diff

  // Step 6: Return the minimum difference
  return min_diff

C++ code for Chocolate Distribution Problem

Here's an example of C++ code to solve the chocolate distribution problem using a greedy algorithm:

#include<iostream>
#include<algorithm> 
#include<climits>
using namespace std;

int findMinDiff(int arr[], int n, int m) {
    // Sort the array in non-decreasing order
    sort(arr, arr + n);

    // Initialize two pointers
    int start = 0;
    int end = m - 1;

    // Initialize minimum difference
    int min_diff = INT_MAX;

    // Move the pointers to minimize the minimum difference
    while (end < n) {
        int diff = arr[end] - arr[start];
        if (diff < min_diff) {
            min_diff = diff;
        }
        start++;
        end++;
    }

    // Return the minimum difference
    return min_diff;
}

int main() {
    int arr[] = {3, 4, 1, 9, 56, 7, 9, 12}; //number of chocolates in each packet
    int n = sizeof(arr) / sizeof(arr[0]); //number of packets
    int m = 5; //number of children
    int min_diff = findMinDiff(arr, n, m);
    cout << "Minimum difference: " << min_diff << endl;
    return 0;
}

Output:

Minimum Difference: 6

Time & Space Complexity

The time complexity to solve the chocolate distribution problem using a greedy algorithm is O(n log n), where n is the number of packets. This is because we use the sort function, which has a worst-case time complexity of O(n log n), and then iterates over the array once, which takes O(n) time. The overall time complexity is therefore dominated by the sort function.

The space complexity of the code is O(n) since we store the array of packet sizes 'a'. Note that the sort function sorts the array in place, so it does not require any additional memory beyond the array itself.

Advantages & Disadvantages

Let's take a look at the advantages of the chocolate distribution problem:

• Fairness: The algorithm distributes chocolate packets in such a way that the difference between the maximum and minimum number of chocolates distributed is minimized. This promotes fairness in the distribution of resources.

• Efficiency: The algorithm has a time complexity of O(n log n) due to the sorting operation at the beginning of the algorithm. This makes it efficient for large input sizes.

• Flexibility: The algorithm can be adapted to solve similar problems where resources need to be distributed fairly among a group of individuals.

But there are some disadvantages as well. The algorithm is specific to the problem of distributing chocolate packets among a group of children. It may not be applicable to other problems that involve resource allocation.

Also, the algorithm uses a greedy approach to minimize the difference between the maximum and minimum number of chocolates distributed. While this approach works well for the chocolate distribution problem, it may not work well for other problems.

Conclusion

Overall, the chocolate distribution problem serves as an interesting and fun problem to test one's mathematical and problem-solving skills. You now can solve the problem using the greedy algorithm with C++.