While searching for a product on any e-commerce website, whenever we want the cheapest product we use the filter 'lowest to highest' resulting in products arranged in increasing order according to their price. How does this happen? It happens because of Sorting. Learn more about Bubble Sort with implementation in Java.
What is Bubble Sort?
Irrespective of the programming language, Sorting techniques are a must to learn as they help you in arranging the objects or numbers in ascending or descending order. Bubble sorting is one of the most basic sorting techniques that helps to arrange the given elements in ascending or descending order.
In Bubble Sort, while traversing the array, each element is compared with the next element and if they aren't in the provided order (ascending or descending), they are swapped. The USP of bubble sort is that when adjacent elements of the array are compared, this results in the largest element reaching its correct position.
That implies the array starts getting sorted from the last indices. The largest element is like a bubble that kind of floats to the end of the array, therefore it is known as bubble sort. The swapping will only and only be done when the compared elements are not in the correct order as how they are shown to be. How? Let's learn through illustration.
How Bubble Sort Algorithm (optimized) Work?
Let's consider the given array and try to arrange this in ascending order using bubble sort.
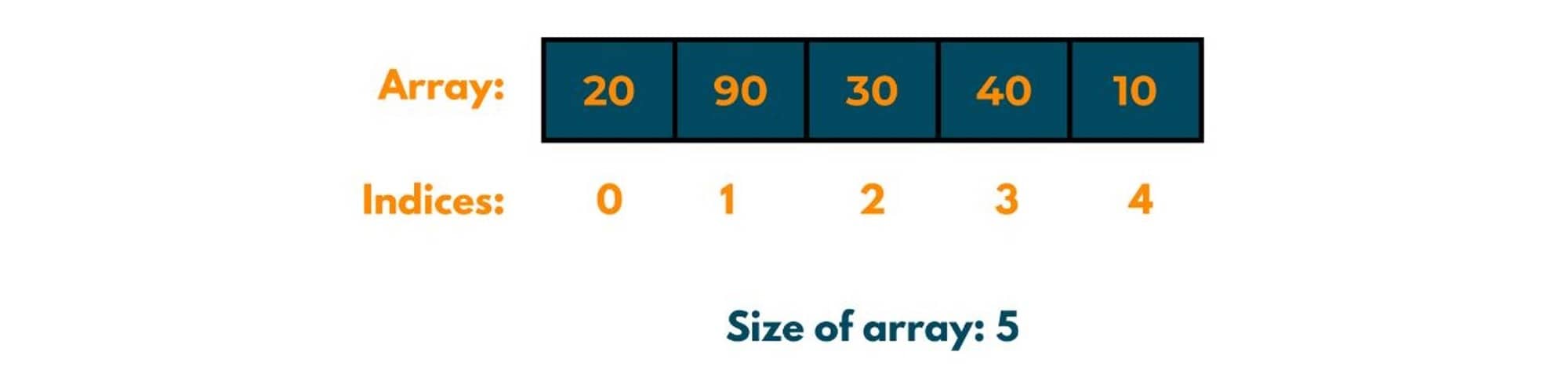
Journey 1:
In 1st journey, all the elements would be compared to the elements that are next to them. In a given array there are 5 elements so, it would take 4 comparisons to compare every adjacent element. So no. of passes in jouney 1 = 4 (or n-1).
Pass 1:
The 0th index element is compared to the 1st index element i.e. 20 is being compared to 90. As we need to arrange the array in ascending order and 20 < 90, therefore, no swapping occurs.

Pass 2:
Now, the 1st index element i.e. 90 would be compared to the 2nd index element i.e. 30. Here, 30 < 90, and as the arrangement to be achieved is in ascending order and for 30 should be positioned before 90, therefore swapping occurs.
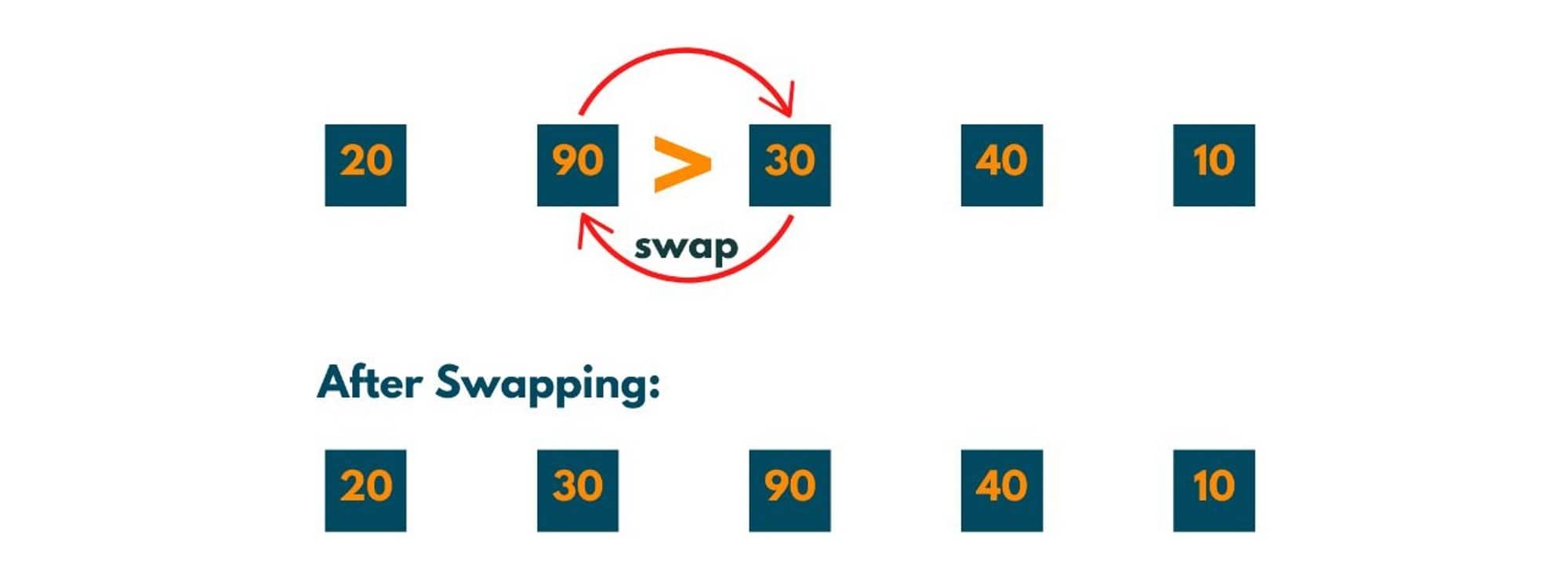
Pass 3:
Now 2nd index element i.e. 90 is compared to 3rd index element i.e. 40. As 90 > 40, swapping occurs.
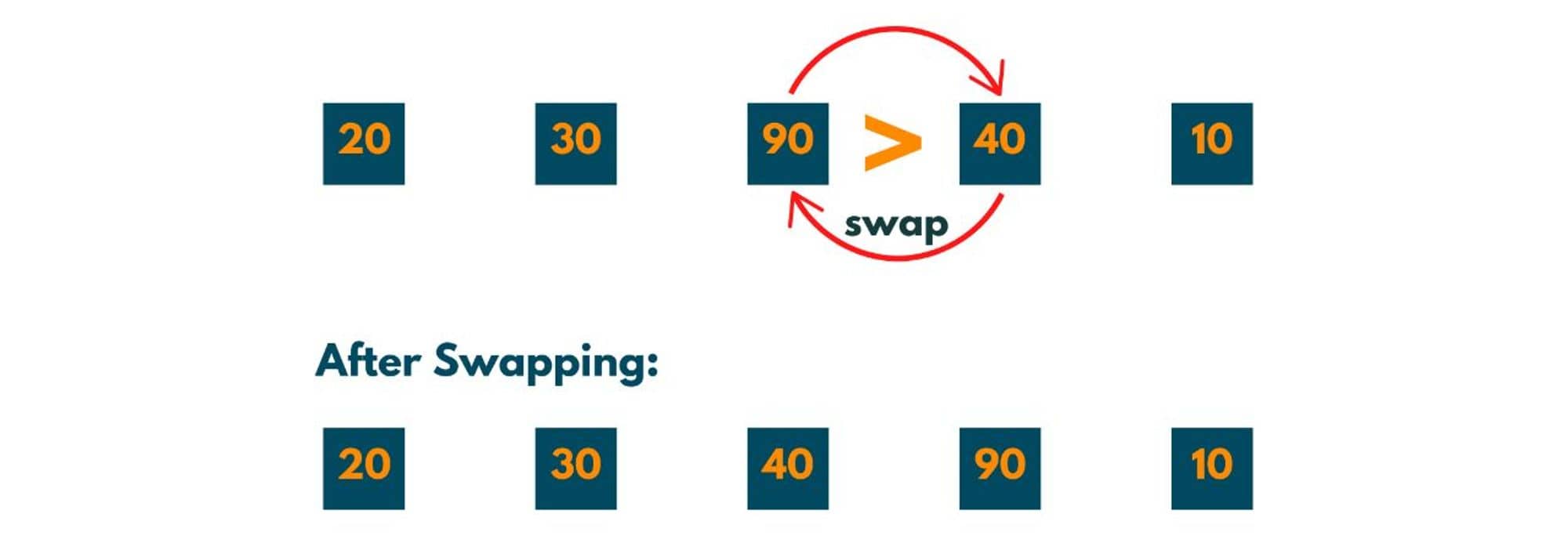
Pass 4:
Now 3rd index element i.e. 90 is compared to the 4th index element i.e. 10. As 90 > 10, swapping occurs.
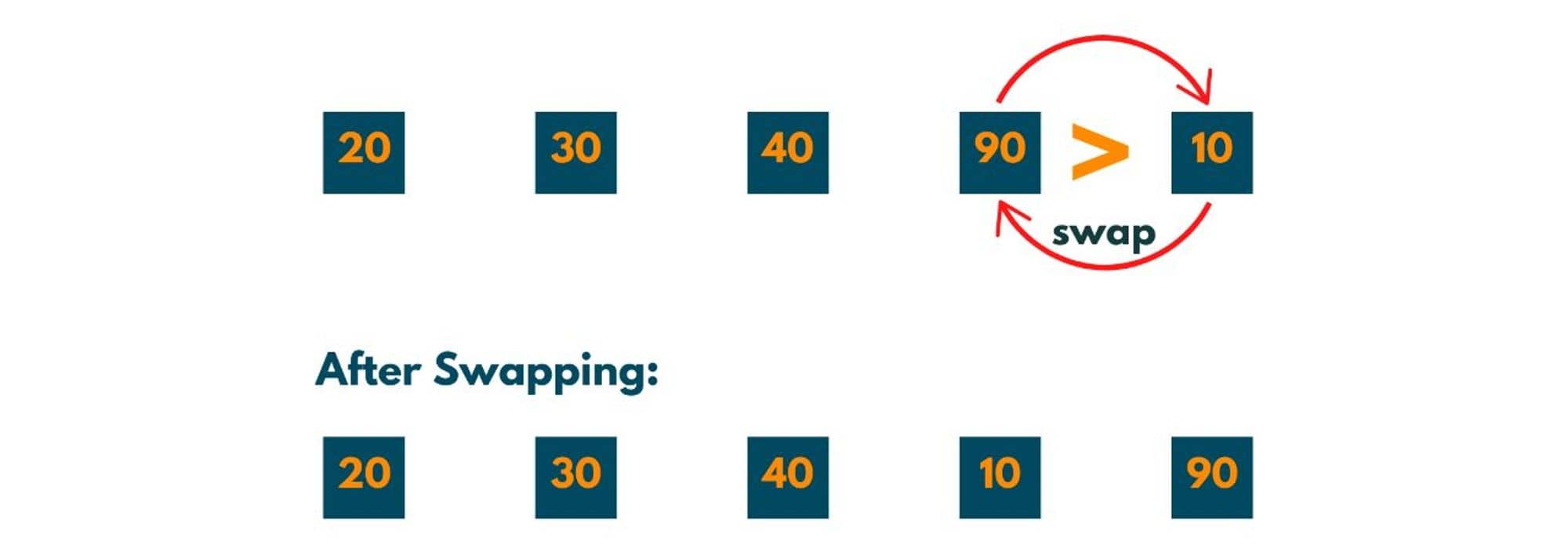
Now all adjacent elements have been compared at least once. This completes Jouney1. But there is something very important to notice i.e. the greatest element of the array has been shifted to the last. That implies the last part of the array is sorted now.

Now as you have noticed that after journey 1, one element reached its correct position. And as there are 5 elements in the array, it would take 4 journeys (i.e n -1) to place 4 elements in their correct position and if 4 elements are at their correct position, the 5th element is automatically at its desired position.
So, no. of jouneys = 4 i.e. length of array - 1.
Journey 2:
As we already know that the last element is sorted, therefore there is no need to compare any adjacent element with it. So, the adjacent elements of the unsorted part only will be compared which takes 3 comparisons or n-2 comparisons. Notice how in each journey no.of comparisons is decreasing.
Pass 1:
The 0th element i.e. 20 is compared to the 1st element i.e. 30. As 20 < 30 that implies the order of elements is correct therefore no swapping occurs.

Pass 2:
The 1st element i.e. 30 is compared to the 2nd element i.e. 40. As 30 < 40 that implies the order of elements is correct therefore no swapping occurs.

Pass 3:
The 2nd element i.e. 40 is compared to the 3rd element i.e. 10. As 40 > 10 that implies the order of elements is not correct therefore swapping occurs.
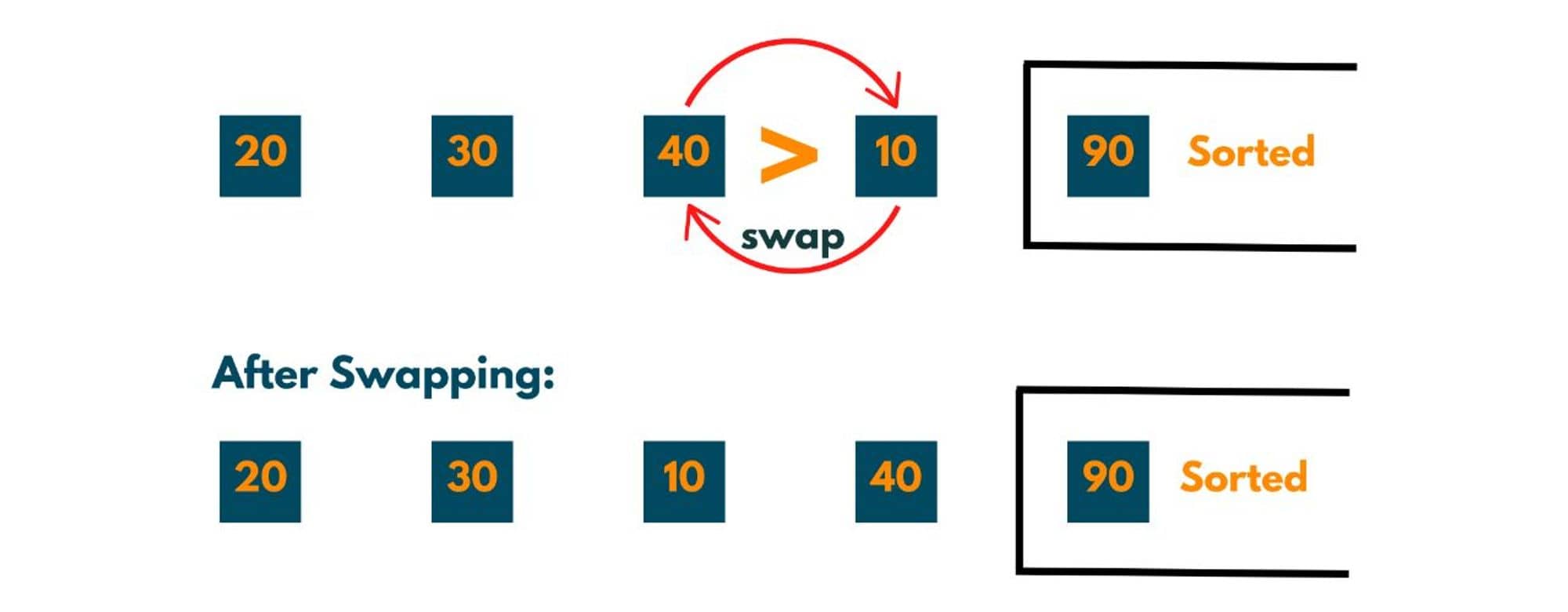
Now all adjacent elements of the unsorted part are compared at least once and we notice here that one more element (the largest element of the unsorted part) reaches its correct position.
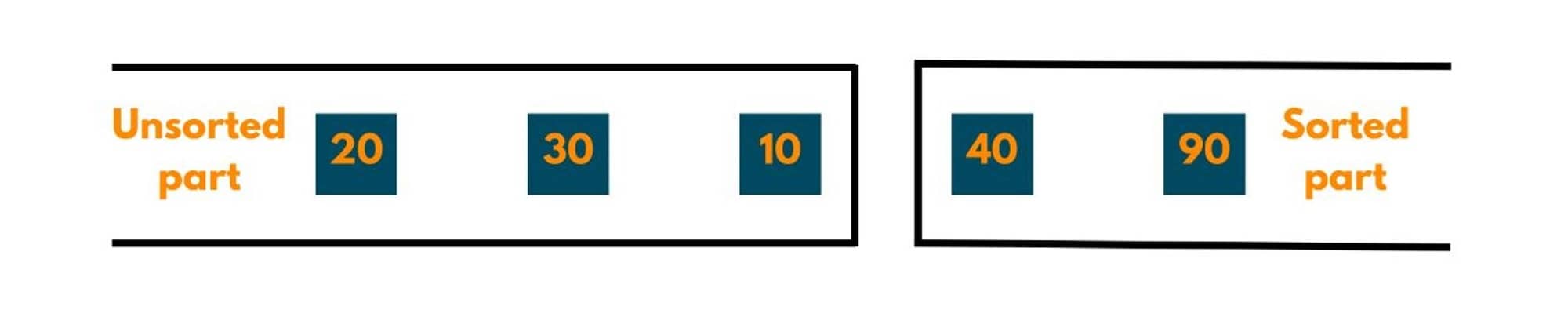
So, after journey 2, two elements are sorted or at their correct position.
Journey 3:
Now the leftover unsorted 3 elements are to be compared with each other. So, no. of comparisons/passes needed would be 2 or n-3.
Pass 1:
The 0th element i.e. 20 is compared to the 1st element i.e. 30. As 20 < 30 that implies the order of elements is correct therefore no swapping occurs.
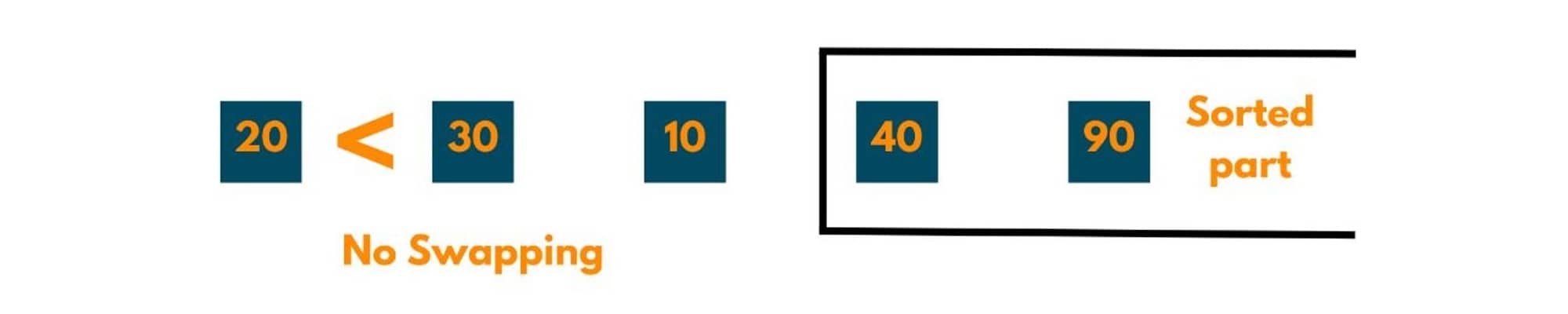
Pass 2:
The 1st element i.e. 30 is compared to the 2nd element i.e. 10. As 30 > 10 that implies the order of elements is not correct therefore swapping occurs.
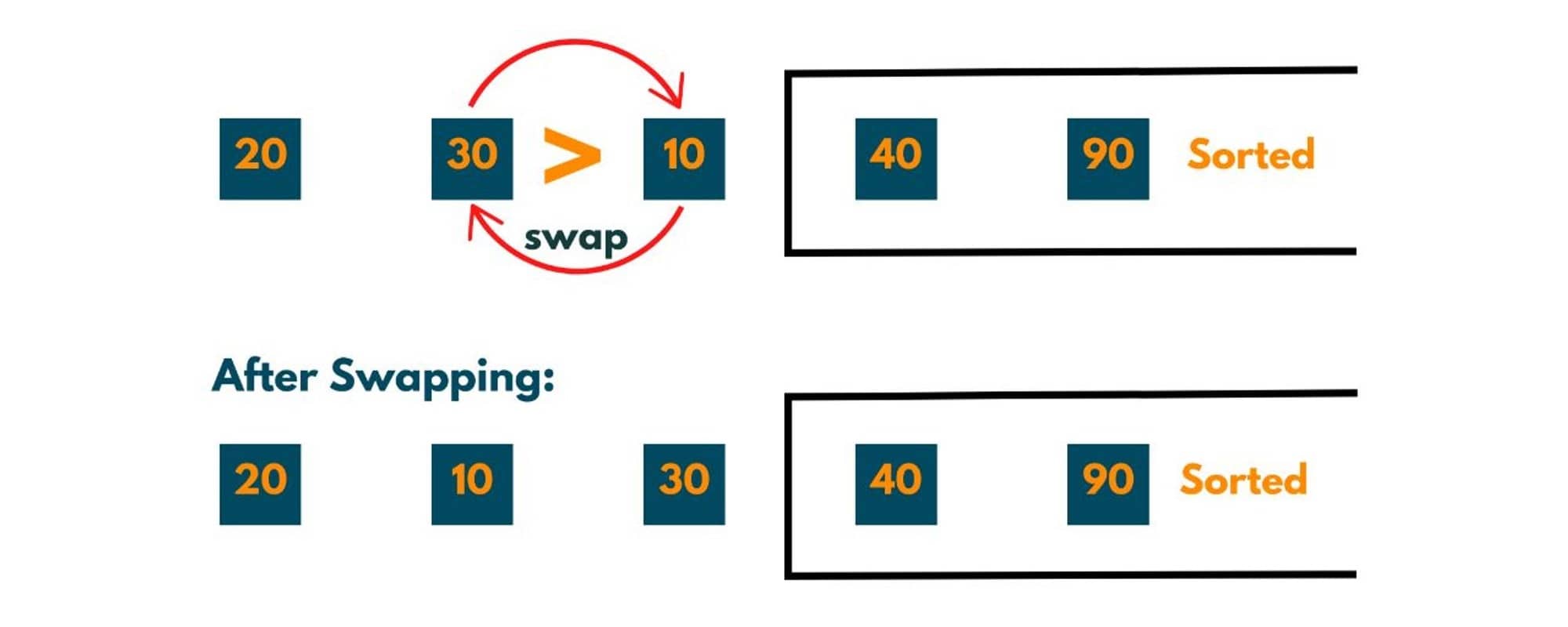
All adjacent elements of the unsorted parts are compared at least once and one more element i.e. 30 reached its correct position.

So elements sorted now = 3 and elements to be sorted = 2.
Journey 4:
Now as only 2 elements are not at their correct position, therefore no. of comparisons or passes = 1.
Pass 1:
The 0th element i.e. 20 is compared to the 1st element i.e. 10. As 20 > 10 that implies the order of elements is not correct therefore swapping occurs.
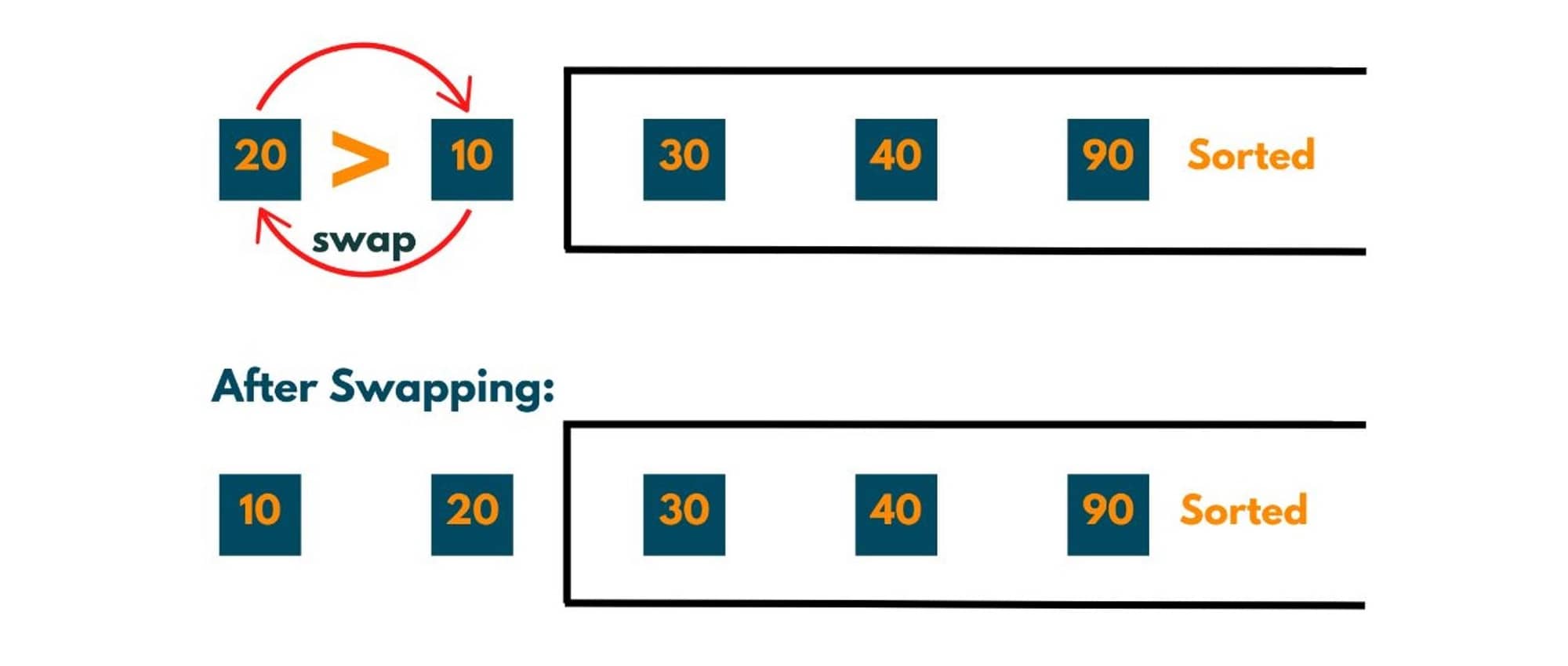
After journey 4, we see that 20 also reaches at its correct position. But the important thing to notice here is, element 10 also reaches its correct position.
In each journey, we were getting an element at its correct position, 4 journeys = 4 elements at their correct position, and when 4 elements are at their right position 5th element is certainly at the desired position. Therefore, there is no need to opt for journey 5.
Important points to notice:
- No. of journeys or iterations (outer loop) = no. of elements in an array (or n) - 1. That implies the iteration count varies from 0 to n-1.
- No. of passes (or inner loop) in journey = n - iteration count - 1.
- Swapping only occurs when an element at a smaller index is greater than an element at a greater index. This simply means elements not in the correct position if to be arranged in ascending order.
Bubble Sort Algorithm (optimized) in Java
Here is the algorithm for bubble sort in Java:
- An outer loop says i, (journeys) from[0, n-1) ( n = length of the array).
- An inner loop say j, from [0, n - outer Loop count - 1).
- if element[j] > element[j+1] -> swap.
Below is the complete code to implement Bubble Sort in Java:
package Sorting; import java.util.*; public class BubbleSort { public static void main(String[] args) { Scanner scn = new Scanner(System.in); int num = scn.nextInt(); int [] arr = new int [num]; for(int i = 0; i < num; i++) { arr[i] = scn.nextInt(); } bubbleSort(arr); System.out.println ("Sorted array is:"); for(int var:arr) { System.out.print(var +" "); } } public static int [] bubbleSort(int [] arr) { // n contains the value of elements or length of array int n =arr.length; boolean flag = false; // outer loop i.e no. of journeys for(int i = 0 ; i < n; i++) { int journey = i+1; System.out.println("Jouney: "+ journey); //inner loop i.e no. of passes for(int j = 0; j < n - 1; j++) { int pass = j+1; System.out.println("Pass: "+ pass); //printing the elements that are being compared System.out.println("Comparing " + arr[j] + " and " + arr[j+1]); if(arr[j] > arr[j+1]) { swap(arr,j,j+1,flag); } } //checking if swapping happened in 1st pass or not if (flag == false) { return arr; } //if flag is false that implies no swapping happened and if no swapping happens it means array is already sorted System.out.println(); } return arr; } public static void swap(int[] arr, int i , int j, boolean flag) { //if swapping happens flag = true; System.out.println("Swapping " + arr[i] + " and " + arr[j]); int temp = arr[i]; arr[i]=arr[j]; arr[j]=temp; } }
Output:
5 20 90 30 40 10 Jouney: 1 Pass: 1 Comparing 20 and 90 Pass: 2 Comparing 90 and 30 Swapping 90 and 30 Pass: 3 Comparing 90 and 40 Swapping 90 and 40 Pass: 4 Comparing 90 and 10 Swapping 90 and 10 Jouney: 2 Pass: 1 Comparing 20 and 30 Pass: 2 Comparing 30 and 40 Pass: 3 Comparing 40 and 10 Swapping 40 and 10 Jouney: 3 Pass: 1 Comparing 20 and 30 Pass: 2 Comparing 30 and 10 Swapping 30 and 10 Jouney: 4 Pass: 1 Comparing 20 and 10 Swapping 20 and 10 Sorted array is: 10 20 30 40 90
How does unoptimized bubble sort work?
As we can notice that in the above implementation of bubble sort, there are some optimizations that were done. We took into count that in each journey one element is getting sorted, according to which we optimized the no. of passes and journeys.
If we take no. of journey = no. of elements of the array and in each journey, we compare all adjacent elements then this takes us to the unoptimized implementation of bubble sort. In an unoptimized implementation, we even compare the elements that are there in the sorted part of the array.
Below is the simple bubble sort implementation:
package Sorting; import java.util.*; public class BubbleSort { public static void main(String[] args) { Scanner scn = new Scanner(System.in); int num = scn.nextInt(); int [] arr = new int [num]; for(int i = 0; i < num; i++) { arr[i] = scn.nextInt(); } bubbleSort(arr); System.out.println ("Sorted array is:"); for(int var:arr) { System.out.print(var +" "); } } public static int [] bubbleSort(int [] arr) { // n contains the value of elements or length of array int n =arr.length; // outer loop i.e no. of journeys for(int i = 0 ; i < n; i++) { int journey = i+1; System.out.println("Jouney: "+ journey); //inner loop i.e no. of passes for(int j = 0; j < n - 1; j++) { int pass = j+1; System.out.println("Pass: "+ pass); //printing the elements that are being compared System.out.println("Comparing " + arr[j] + " and " + arr[j+1]); if(arr[j] > arr[j+1]) { swap(arr,j,j+1); } } System.out.println(); } return arr; } public static void swap(int[] arr, int i , int j) { System.out.println("Swapping " + arr[i] + " and " + arr[j]); int temp = arr[i]; arr[i]=arr[j]; arr[j]=temp; } }
Output:
5 20 90 30 40 10 Jouney: 1 Pass: 1 Comparing 20 and 90 Pass: 2 Comparing 90 and 30 Swapping 90 and 30 Pass: 3 Comparing 90 and 40 Swapping 90 and 40 Pass: 4 Comparing 90 and 10 Swapping 90 and 10 Jouney: 2 Pass: 1 Comparing 20 and 30 Pass: 2 Comparing 30 and 40 Pass: 3 Comparing 40 and 10 Swapping 40 and 10 Pass: 4 Comparing 40 and 90 Jouney: 3 Pass: 1 Comparing 20 and 30 Pass: 2 Comparing 30 and 10 Swapping 30 and 10 Pass: 3 Comparing 30 and 40 Pass: 4 Comparing 40 and 90 Jouney: 4 Pass: 1 Comparing 20 and 10 Swapping 20 and 10 Pass: 2 Comparing 20 and 30 Pass: 3 Comparing 30 and 40 Pass: 4 Comparing 40 and 90 Jouney: 5 Pass: 1 Comparing 10 and 20 Pass: 2 Comparing 20 and 30 Pass: 3 Comparing 30 and 40 Pass: 4 Comparing 40 and 90 Sorted array is: 10 20 30 40 90
Time and Space Complexity
The total time taken for the program to sort an array would be the sum of the time taken to do comparisons and the time taken to sort the members. Taking k(n) to be time taken for n comparisons and T(n) be time taken to sort n members. So, T(n) can be denoted as:
T(n) = k(n-1) + T(n-1)
T(n-1) = k(n-2) + T(n-2)
T(n-2) = k(n-3) + T(n-3)
----------------------------
----------------------------
T(2) = k
This all sums up to:-
T(n) = k[(n-1) + (n-2) + (n-3) + ----- + 1)
T(n) = [k * n * (n-1)]/2
T(n) is directly proportional to O(n^2).
- Worst-case Scenario: When the array elements are arranged in reverse order, it takes O([n * (n-1)]/2 ).
- Average case scenario: Time complexity for arranging a completely random array in any order is again O(n^2) as total swaps average out to be n^2 / 4.
- Best Case Scenario: When an array is already arranged in the correct order, there is no need to do any swaps, and therefore we get to know in one traversal that the array is already sorted.
So time complexity comes out to be O(n). And as we are not using any additional space of memory except the input array, therefore space complexity comes out to be O(1).
Is Bubble Sort a stable sorting technique?
A stable sorting technique is one in which the relative order of elements is maintained. Say, If two elements are equal, then their order of occurrence will remain the same after sorting i.e. if one is at the 2nd index and the other is at the 3rd index that implies after sorting, the element which was at the 2nd index will be 1 index ahead of element at 3rd index.
The image below illustrates this well.
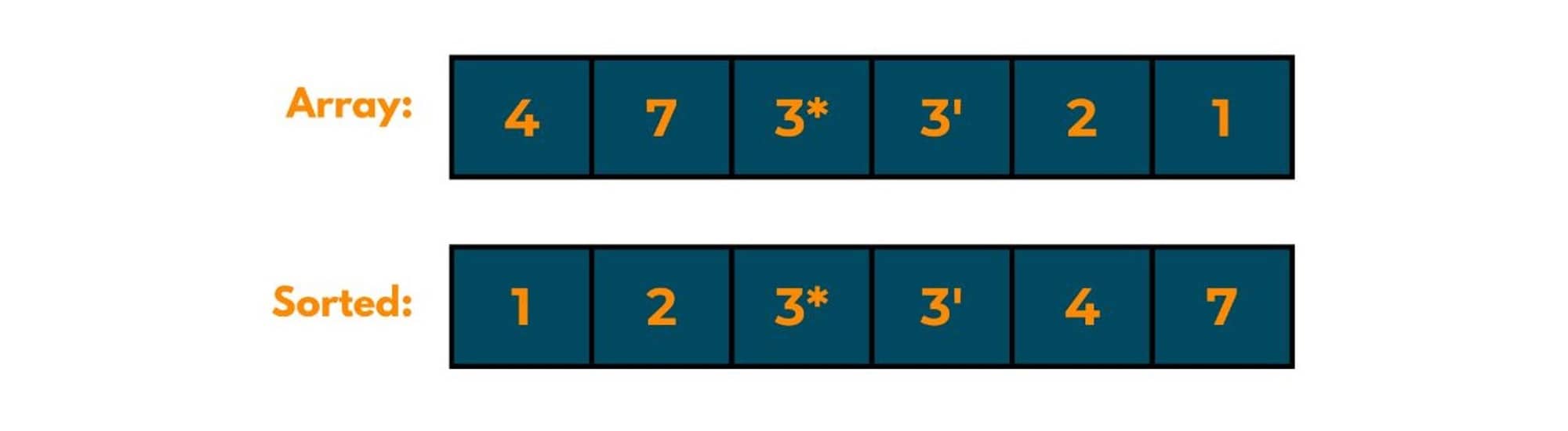
If we closely consider the working of the bubble sort algorithm, we will notice that as adjacent swapping is only being done, the relative order of equal elements doesn't change. So bubble sorting is a stable sorting technique.
Is Bubble Sort an in-place algorithm?
An in-place algorithm is one in which the changes happen in the input array only and no additional memory is used except for the input array. As bubble sort uses no extra space, it is an in-place algorithm.
Can bubble sort be implemented recursively?
If you want a recursive implementation of bubble sort, here is the algorithm:- A function will be created called "recursiveBubbleSort" and we will pass the numberOfElements to be compared and the array.
- This function acts as an outer loop of iterative bubble sort, as this function governs no. of elements to be compared or no. of journeys and we pass one element less each time to this function.
- When n==1, we return as we reach the base case.
- Inside the function, we compare adjacent elements just like the inner loop of an iterative algorithm.
Get the code here:
import java.util.*; public class BubbleSort { public static void main(String[] args) { Scanner scn = new Scanner(System.in); int num = scn.nextInt(); int [] arr = new int [num]; for(int i = 0; i < num; i++) { arr[i] = scn.nextInt(); } recursiveBubbleSort(arr, arr.length); System.out.println ("Sorted array is:"); for(int var:arr) { System.out.print(var +" "); } } public static void recursiveBubbleSort(int[] arr, int n) { // base case when no. of elements to be compared = 1 if( n == 1) { return; } //comparing adjacent elements for(int j = 0 ; j < n - 1; j++) { if(arr[j] > arr[j + 1]) { int temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } recursiveBubbleSort(arr,n-1); } }
Output:
5 8 7 12 1 22 Sorted array is: 1 7 8 12 22
Conclusion
Bubble Sort in Java is a very basic and easiest sorting technique as it effortlessly sorts elements and helps beginners to learn the basics of sorting. After one easily understands it, one can use this approach to any other question which might not be of this type.








