A binary tree is a widely used data structure in computer science that consists of nodes connected hierarchically. The bottom view of a binary tree provides valuable insights into its structure when viewed from a vertical perspective. In this article, we will understand the concept of the bottom view of a binary tree, and present an algorithm to obtain the bottom view with examples.
What is the Bottom View of a Binary Tree?
The bottom view of a binary tree refers to the set of nodes that are visible when the tree is observed from the bottom. Each node in the bottom view is associated with its horizontal distance from the root of the tree. Nodes sharing the same horizontal distance are considered at the same level, and the node with the highest level (closest to the bottom) is included in the bottom view.
But do we need to print the bottom view? Well, the bottom view provides an intuitive visual representation of the binary tree, emphasizing the nodes at the lowest levels. It can be employed to extract essential information, such as the last visible node at each horizontal distance.
Let's consider the following binary tree:
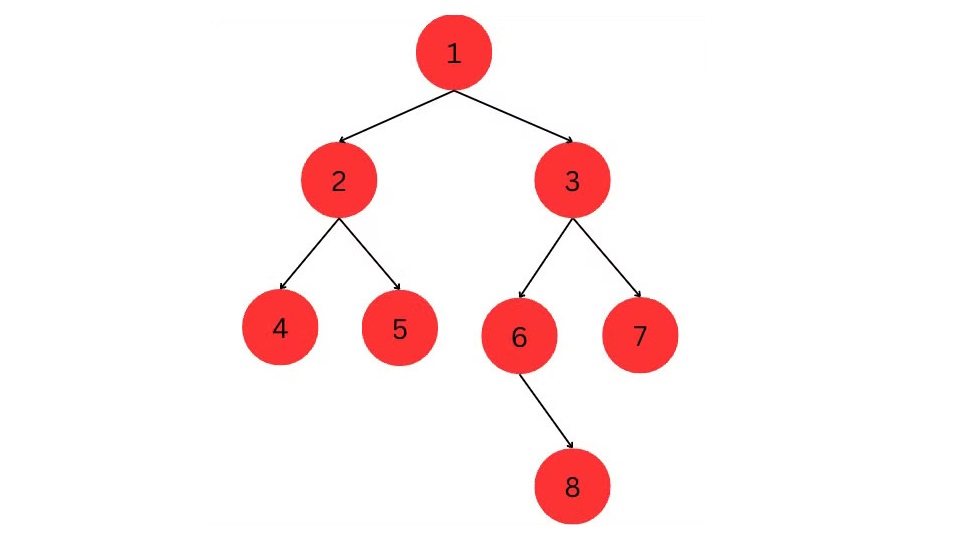
The bottom view of this binary tree, from left to right, would be: 4, 2, 6, 8, 7. These nodes are the last visible nodes at their respective horizontal distances when viewed from the bottom.
Approaches to Obtain the Bottom View
To find the bottom view of a binary tree, you can employ various traversal algorithms, including Depth-First Search (DFS), Breadth-First Search (BFS), and Level Order Traversal.
Let's explore how each of these methods can be used to determine the bottom view of a binary tree:
Depth-First Search (DFS)
DFS is a traversal algorithm that explores as far as possible along each branch before backtracking. In the context of finding the bottom view of a binary tree, you can use either the pre-order, in-order, or post-order traversal technique. However, the pre-order traversal is typically preferred.
Pre-order DFS Algorithm:
- Start with the root node.
- Traverse the left subtree recursively.
- Traverse the right subtree recursively.
- While traversing, maintain a horizontal distance for each node and keep track of the maximum and minimum horizontal distances.
- Store the node's value and horizontal distance in a map or dictionary.
- After traversing the entire tree, extract the values associated with the maximum horizontal distance for each level. These values represent the bottom view of the binary tree.
Here is the code:
#include #include using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} }; void dfs(TreeNode* root, int horizontalDistance, int level, map<int, pair<int, int>>& nodeMap) { if (root == nullptr) return; if (nodeMap.count(horizontalDistance) == 0 || level >= nodeMap[horizontalDistance].second) { nodeMap[horizontalDistance] = make_pair(root->val, level); } dfs(root->left, horizontalDistance - 1, level + 1, nodeMap); dfs(root->right, horizontalDistance + 1, level + 1, nodeMap); } void printBottomView(TreeNode* root) { map<int, pair<int, int>> nodeMap; // map to store horizontal distance, (value, level) dfs(root, 0, 0, nodeMap); for (const auto& entry : nodeMap) { cout << entry.second.first << " "; } } int main() { // Create a sample binary tree TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); root->right->left->right = new TreeNode(8); // Find and print the bottom view cout << "Bottom View: "; printBottomView(root); return 0; }
Output:
Bottom View: 4 2 6 8 7
The Time Complexity is O(n), where n is the number of nodes in the binary tree. Since we visit each node exactly once, the time complexity is linear.
Breadth-First Search (BFS)
BFS is a traversal algorithm that explores all the nodes at the same level before moving to the next level. This algorithm is well-suited for finding the bottom view of a binary tree.
BFS Algorithm:
- Start with the root node and enqueue it into a queue.
- Maintain a dictionary or map to store the horizontal distance of each node from the root.
- While the queue is not empty:
- Dequeue a node and update its horizontal distance in the dictionary.
- Enqueue its left child (if present) with a decreased horizontal distance.
- Enqueue its right child (if present) with an increased horizontal distance.
- After traversing the entire tree, extract the values associated with the largest horizontal distance for each level. These values represent the bottom view of the binary tree.
Here is the code:
#include #include #include using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} }; void printBottomView(TreeNode* root) { if (root == nullptr) return; map<int, int> nodeMap; // map to store horizontal distance, value queue<pair<TreeNode*, int>> q; // queue to perform BFS q.push(make_pair(root, 0)); while (!q.empty()) { TreeNode* node = q.front().first; int horizontalDistance = q.front().second; q.pop(); nodeMap[horizontalDistance] = node->val; if (node->left) q.push(make_pair(node->left, horizontalDistance - 1)); if (node->right) q.push(make_pair(node->right, horizontalDistance + 1)); } for (const auto& entry : nodeMap) { cout << entry.second << " "; } } int main() { // Create a sample binary tree TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); root->right->left->right = new TreeNode(8); // Find and print the bottom view cout << "Bottom View: "; printBottomView(root); return 0; }
Output:
Bottom View: 4 2 6 8 7
The Time Complexity is O(n), where n is the number of nodes in the binary tree. Since we visit each node exactly once, the time complexity is linear.
Level Order Traversal
Level order traversal visits nodes level by level, starting from the root and moving to the next level before visiting the nodes in that level.
Level Order Traversal Algorithm:
- Start with the root node and enqueue it into a queue.
- Maintain a dictionary or map to store the horizontal distance of each node from the root.
- While the queue is not empty:
- Dequeue a node and update its horizontal distance in the dictionary.
- Enqueue its left child (if present).
- Enqueue its right child (if present).
- After traversing the entire tree, extract the values associated with the largest horizontal distance for each level. These values represent the bottom view of the binary tree.
Here is the code:
#include #include #include using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} }; void printBottomView(TreeNode* root) { if (root == nullptr) return; map<int, int> nodeMap; // map to store horizontal distance, value queue<pair<TreeNode*, int>> q; // queue to perform level order traversal q.push(make_pair(root, 0)); while (!q.empty()) { TreeNode* node = q.front().first; int horizontalDistance = q.front().second; q.pop(); nodeMap[horizontalDistance] = node->val; if (node->left) q.push(make_pair(node->left, horizontalDistance - 1)); if (node->right) q.push(make_pair(node->right, horizontalDistance + 1)); } for (const auto& entry : nodeMap) { cout << entry.second << " "; } } int main() { // Create a sample binary tree TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); root->right->left->right = new TreeNode(8); // Find and print the bottom view cout << "Bottom View: "; printBottomView(root); return 0; }
Output:
Bottom View: 4 2 6 8 7
The Time Complexity is O(n), where n is the number of nodes in the binary tree. Since we visit each node exactly once, the time complexity is linear.
Conclusion
Overall, understanding the bottom view of a binary tree lets you see what nodes are visible if you were looking from below the tree. When you’re preparing for coding interviews, learning this concept can give you a nice edge.








