In Tree-based models, there is a criterion for selecting the best split-feature based on which the root of say, a Decision Tree gets split into child nodes (sub-samples of the total data in the root and so on) and hence, a decision is made. So, in a Decision Tree split-feature is the judge and child nodes represent the judgements. The basic intuition of finding the best split of the root or any internal node of a Decision Tree is that, the each of the child nodes to be created, should be as homogeneous as possible. In other words, the each of the child nodes to be created should have most of the instances with target labels belonging to the same class. In order to achieve so, there are 2 most popular criteria which is very common among Machine Learning practitioners:
1. Gini Impurity
2. Entropy and Information Gain
In this article, the criterion, Gini Impurity and it's application in Tree-based Models is discussed.
All you need to know about Gini Impurity
Gini Index
Gini Index is a popular measure of data homogeneity. Data Homogeneity refers to how much polarized is the data to a particular class or category. Let us consider an example of an Exploratory Analyzed Data of people winning or losing a tournament, given their Age and Gender:
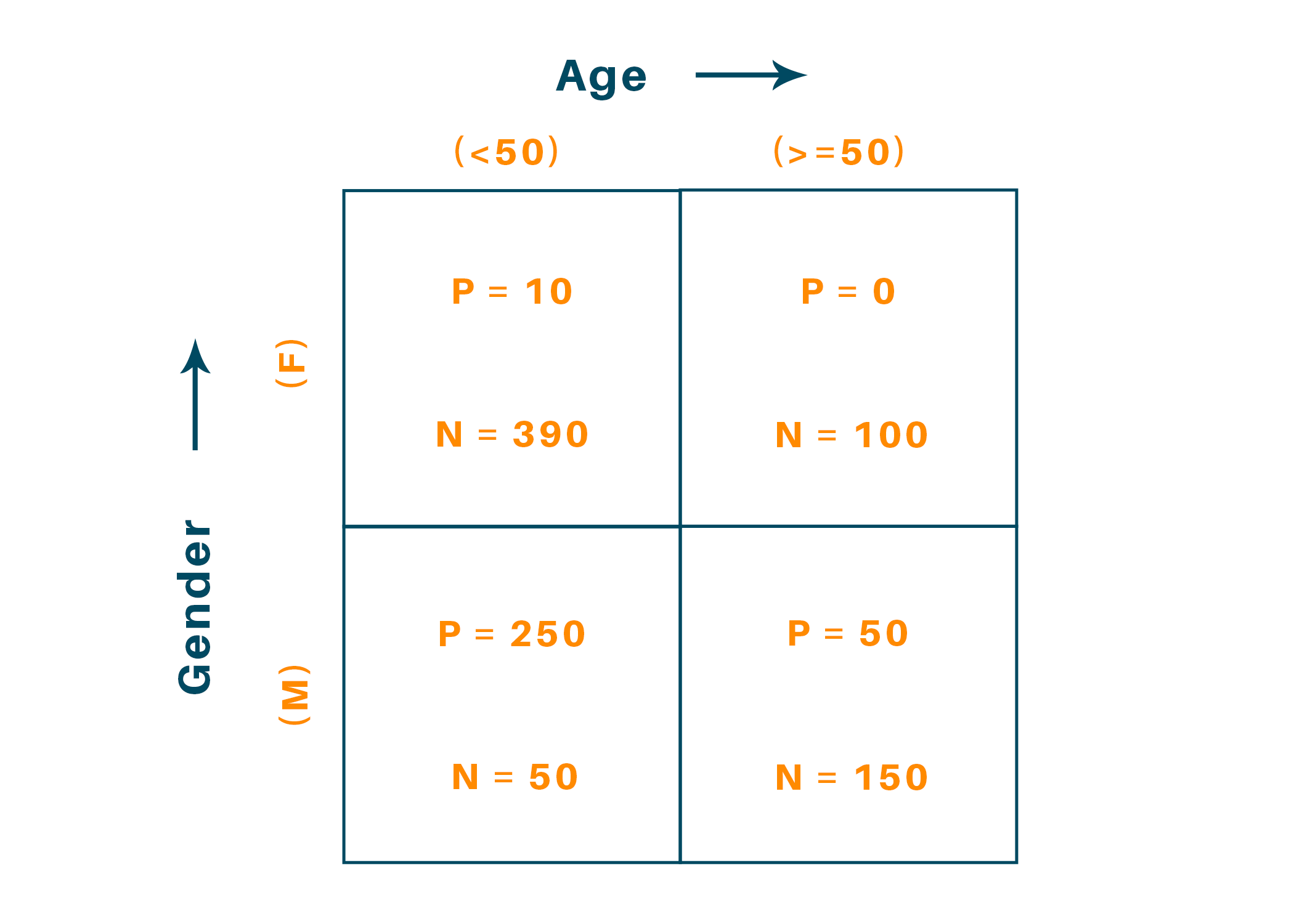
So, there are 4 blocks of analyzed data. The labels 'P' and 'N' indicate number of wins and losses respectively.
Gini Index (GI) is defined as,
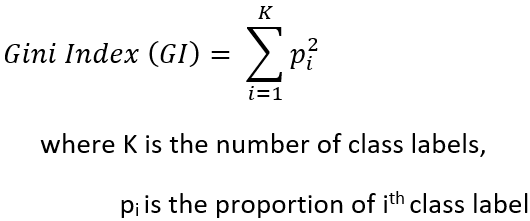
From the definition, it is evident that for perfectly homogeneous data block, the Gini Index is equal to 1.
Now, in this example, there are 2 features, Gender and Age and the target label is win/loss i.e., outcome of the tournament. GI is calculated for each and every feature and the feature with the highest value is to selected as the best split-feature.
For calculating the Gini Index for Gender, Gini Index of Male (M) and Female (F) categories need to be calculated
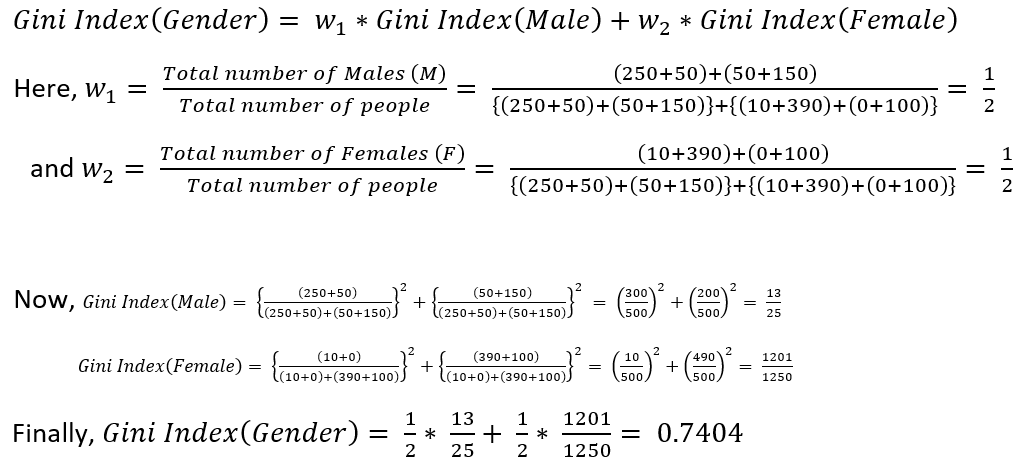
Similarly, for calculating the Gini Index of Age, Gini Index of labels '<50' i.e., age less than 50 and '>=50' i.e., age greater than or equal to 50 need to be calculated
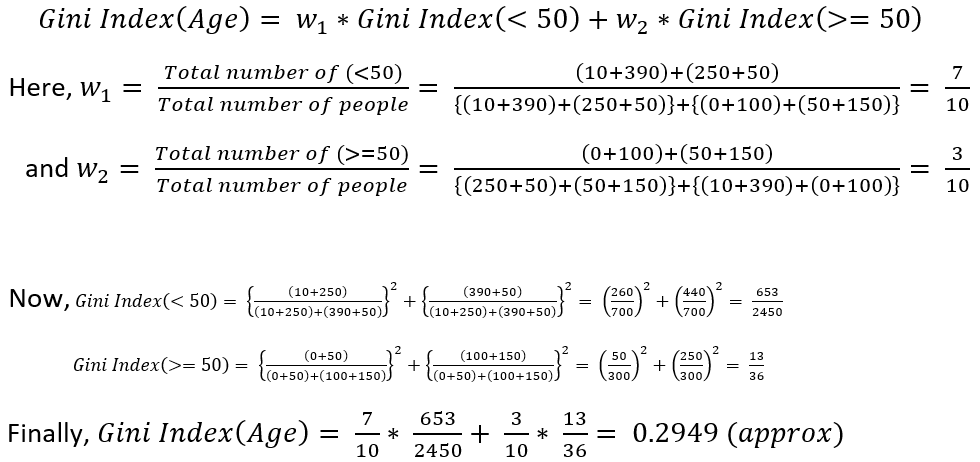
So, as Gini Index(Gender) is greater than Gini Index(Age), hence, Gender is the best split-feature as it produces more homogeneous child nodes.
Gini Impurity
Now, Gini Impurity is just the reverse mathematical term of Gini Index and is defined as,
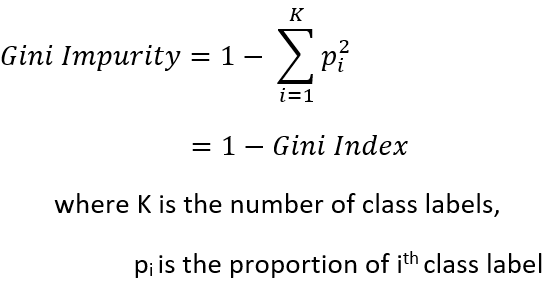
So, it is a measure of anti-homogeneity and hence, the feature with the least Gini Impurity is selected to be the best split feature.
Now, following the above example, Gini Impurity can be directly calculated for each and every feature.
Calculating Gini Impurity for Gender, Gini Impurity of Male (M) and Female (F) need to be calculated

Similarly, for calculating the Gini Impurity of Age, Gini Impurity of labels '<50' i.e., age less than 50 and '>=50' i.e., age greater than or equal to 50 need to be calculated
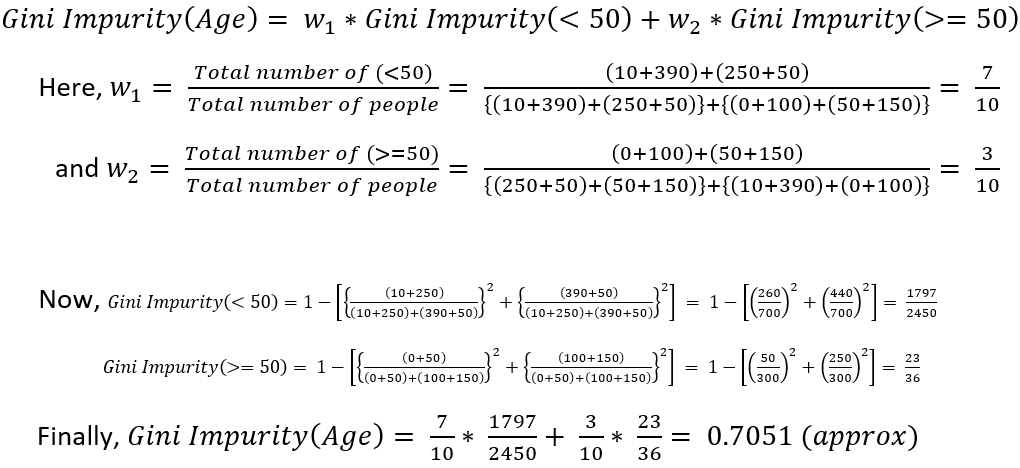
So, as Gini Impurity(Gender) is less than Gini Impurity(Age), hence, Gender is the best split-feature.
Conclusion
So, in this way, Gini Impurity is used to get the best split-feature for the root or any internal node (for splitting at any level), not only in Decision Trees but any Tree-Model.




.png)


