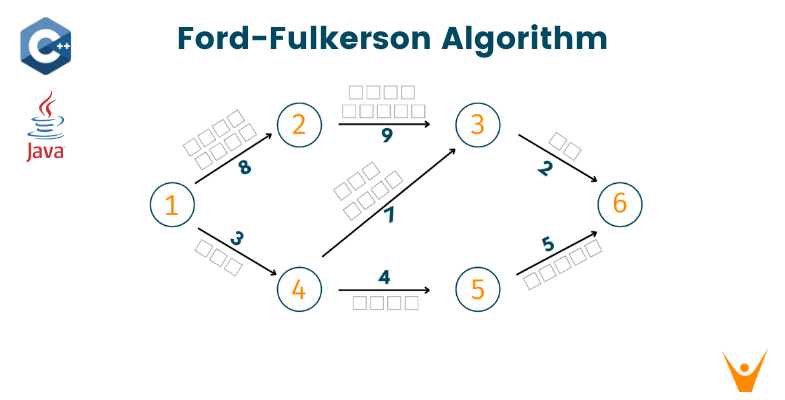
With a huge number of people working towards technological development, complex problems are bound to come up. Thus, experts all over the world are continuously devising specific algorithms to tackle particular types of questions. One such algorithm is Ford Fulkerson Algorithm. In this blog, we shall discuss its implementation in C++ & Java.
What is Ford-Fulkerson Algorithm?
Ford-Fulkerson Algorithm is a set of steps that we follow to tackle the max-flow min-cut problem. It uses a greedy approach to find the maximum flow coming out of a flow network. Discovered in 1956 by Ford and Fulkerson, this algorithm tackles the above-stated problem in a very neat way.
Don't know what the max-flow min-cut problem is? Don't worry, let's start from the beginning.
What is Max-Flow Min-Cut Problem?
You are given a graph that represents a network flow as illustrated in the given image. Every edge of this network has a certain capacity. You are also given 2 special vertices called source 's' and sink 't'. Now, you need to find the maximum possible flow from source to sink with the following constraints:
- The flow specified for an edge does not exceed its capacity.
- The net incoming flow should be equal to the net outgoing flow except for s and t.
To understand the intuition behind this, first, let's go through some terminologies that we'll be using throughout.
-
Augmenting Path: The multiple paths available in the flow network.
-
Residual Graph: The flow network that has additional flow.
- Residual Capacity: The capacity of flow left in the edge after subtracting the flow.
Ford-Fulkerson Approach with an Example
The intuition behind solving this problem is quite simple. Let's understand this with the help of an example.
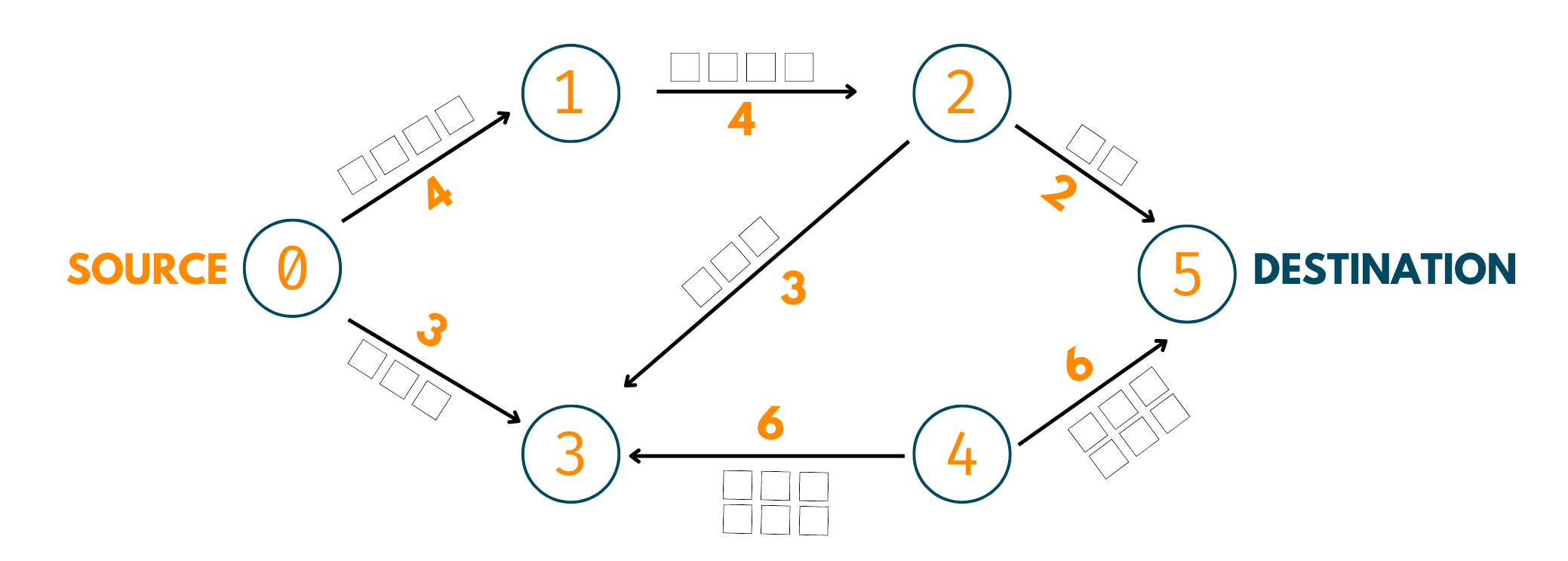
Imagine you have a network of roads from where daily certain cars travel. Take a look at below car network. Now, obviously, the roads cannot be infinitely wide, thus, they all have a fixed width that ensures only a certain number of cars travel through them at a time.
There is a starting point and a destination as well. The cars always start from the starting point and have to reach the destination. But, there are several paths to take. Let's start sending cars one by one to all the roads.
1. 0->1->2->5
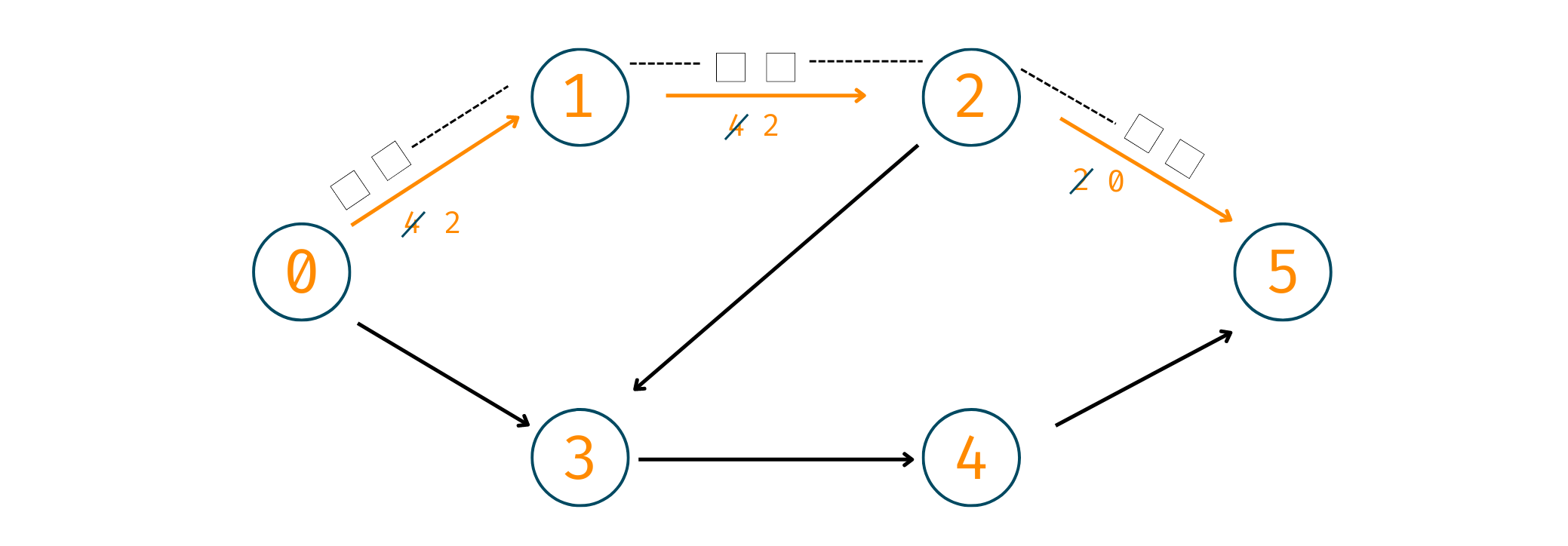
Here, you'll start by sending 2 cars for 0->1. Why? Although this road's capacity is 4 if we look further, only 2 cars can pass through 2->5. Therefore, we take 2 here. Now, 2 cars have reached their destination.
Cars Reached = 2
2. 0->3->4->5
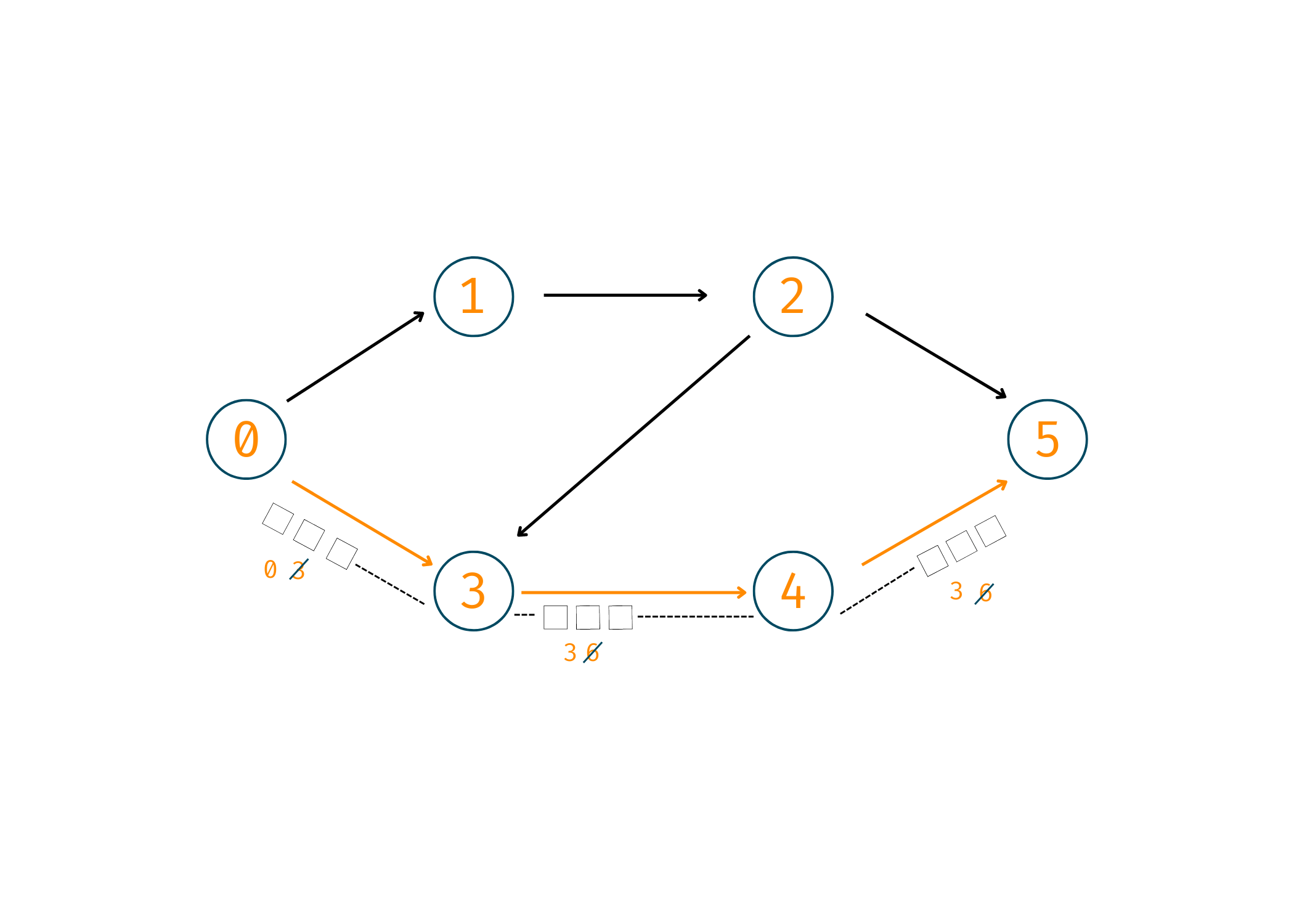
Now, here you'll take 3 cars and make them reach the destination by following the path mentioned.
Cars Reached = 2+3 = 5
3. 0->1->2->3->4->5
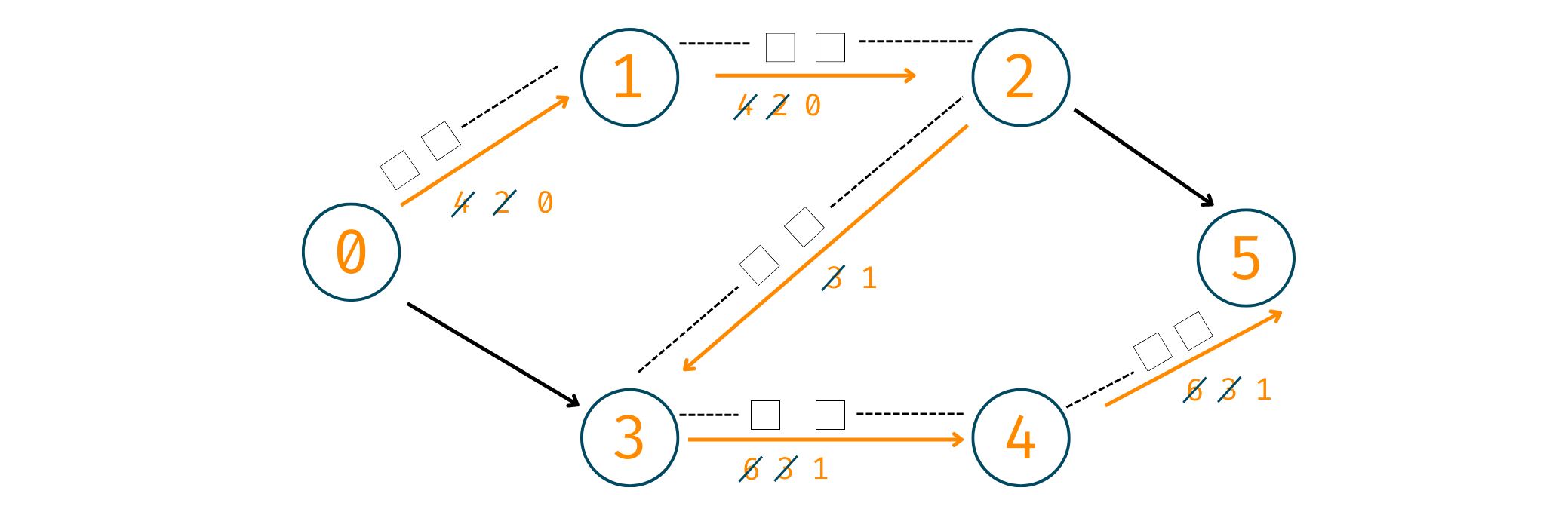
Now, 2 cars have already gone through road 0->1 and 1->2, therefore, we'll take the remaining cars, that is, 2. Similarly, on road 2->3 we have a residual capacity of 3 so, after traveling of 2 cars, we'll have 1 over there. The same goes for the other 2 roads in this augmenting path.
Cars Reached = 5+2 = 7
Now, although we still have paths left, we don't have any augmented paths. Why? This is because the path starting from the source has ended, the roads have been full to their capacity and thus, we cannot make any more cars travel.
Therefore, the final answer comes out to be 7. In the same way, we process the maximum flow by taking cars as data or any other element.
Steps to Follow
Now that you've understood what to do, it's important that you know how to do it. Below are the steps to be followed to find the maximum flow in a network:
- Initialize the start flow as 0.
- Observe the augmenting path from source to sink.
- Find the max flow from that particular path.
- Add it to the final maximum possible flow.
What is Ford-Fulkerson Algorithm Used for?
The Ford-Fulkerson method is a popular approach for resolving network flow issues. It is employed to determine the maximum flow within a flow network, a directed graph that depicts the movement of a particular commodity across a system of pipes or channels. The algorithm has the names of the two authors who first published it in 1956: L. R. Ford Jr. and D. R. Fulkerson.
The Ford-Fulkerson algorithm begins with a flow of 0, increases it iteratively, and stops when there is no more flow to add. This is how the algorithm operates:
- Set all edges (u, v) in E's flow f(u, v) to 0 at the beginning.
- While the residual graph G' contains an augmenting path p:
- Determine the path's bottleneck capacity, or b(p), which is the combined minimum capacity of all of its edges.
- For all edges in p, increase the flow f(u, v) along path p by b(p).
- The total amount of flows f(u, v) exiting the source vertex should be returned as the maximum flow.
When there are no more augmenting paths in the residual graph, the process is finished. Depending on how the augmenting path is found will determine how difficult the algorithm is.
Implementation with C++
Here is the C++ implementation for the Ford-Fulkerson Algorithm:
//C++ Program For Ford Fulkerson Algorithm #include #include <bits/stdc++.h> using namespace std; int bfs(int source,int target,int n,vector<int>& parent,vector<vector<int>>& graph){ //Update the parent vector as each node value to be -1 fill(parent.begin(),parent.end(),-1); //parent of source node to be -2 parent[source] = -2; //Initializing queue for storing and min capacity so far queue<pair<int,int>> q; //Source node min capacity to be 1e9 q.push({source,1e9}); //Looping while queue is not empty while(!q.empty()){ //storing top node and min capacity so far int u = q.front().first; int cap = q.front().second; //Removing top node from queue q.pop(); //Looping all edges from u for(int v=0;v<n;v++){ //finding v node has edge from u if(u!=v && graph[u][v]!=0 && parent[v]==-1){ //storing parent v to be u parent[v] = u; //Updating the minimum capacity int min_cap = min(cap,graph[u][v]); //If v is the target node then return minimum capacity if(v==target){ return min_cap; } //if we didn't find target node //Insert the v node and minimum capacity so far in queue q.push({v,min_cap}); } } } //if we didn't find path between source to target return 0 return 0; } int Ford_Fulkerson(int source,int target,int n,vector<vector<int>>& graph){ //Initializing parent vector for finding the path from source to target //In which we add parent of the node vector<int> parent(n,-1); //Initializing maximum flow for storing ans int max_flow = 0; int min_cap = 0; //storing minimum capacity in each path //looping while minimum capacity become zero //For finding path and minimum capacity we call function bfs() while(min_cap = bfs(source,target,n,parent,graph)){ //Adding the min_cap from this path max_flow += min_cap; //storing target node in v int v = target; //while we didn't find the source node //Looping through path stored in parent while(v!=source){ //finding parent of v node int u = parent[v]; //Subtracting minimum capacity from u to v //And adding minimum capacity from v to u graph[u][v] -= min_cap; graph[v][u] += min_cap; //Update the v node to it's parent v=u; } } //Returning maximum flow in the graph return max_flow; } void addEdge(vector<vector<int>>& graph, int u, int v, int w) { graph[u][v] = w; } int main() { //Intializing the graph in 2d vector int V = 6; vector<vector<int>> graph(V, vector<int> (V, 0)); //Adding edges weight in the graph addEdge(graph, 0, 1, 4); addEdge(graph, 0, 3, 3); addEdge(graph, 1, 2, 4); addEdge(graph, 2, 3, 3); addEdge(graph, 2, 5, 2); addEdge(graph, 3, 4, 6); addEdge(graph, 4, 5, 6); //Printing the maximum flow from the given network Using Ford Fulkerson Method cout << "Maximum Flow Using Ford Fulkerson Algo: " << Ford_Fulkerson(0,5,V,graph) << endl; return 0; }
Output:
Maximum Flow Using Ford Fulkerson Algo: 7
Let's take another flow network and find the maximum possible flow using its implementation in Java.
Implementation with Java
The graph we used over here is:
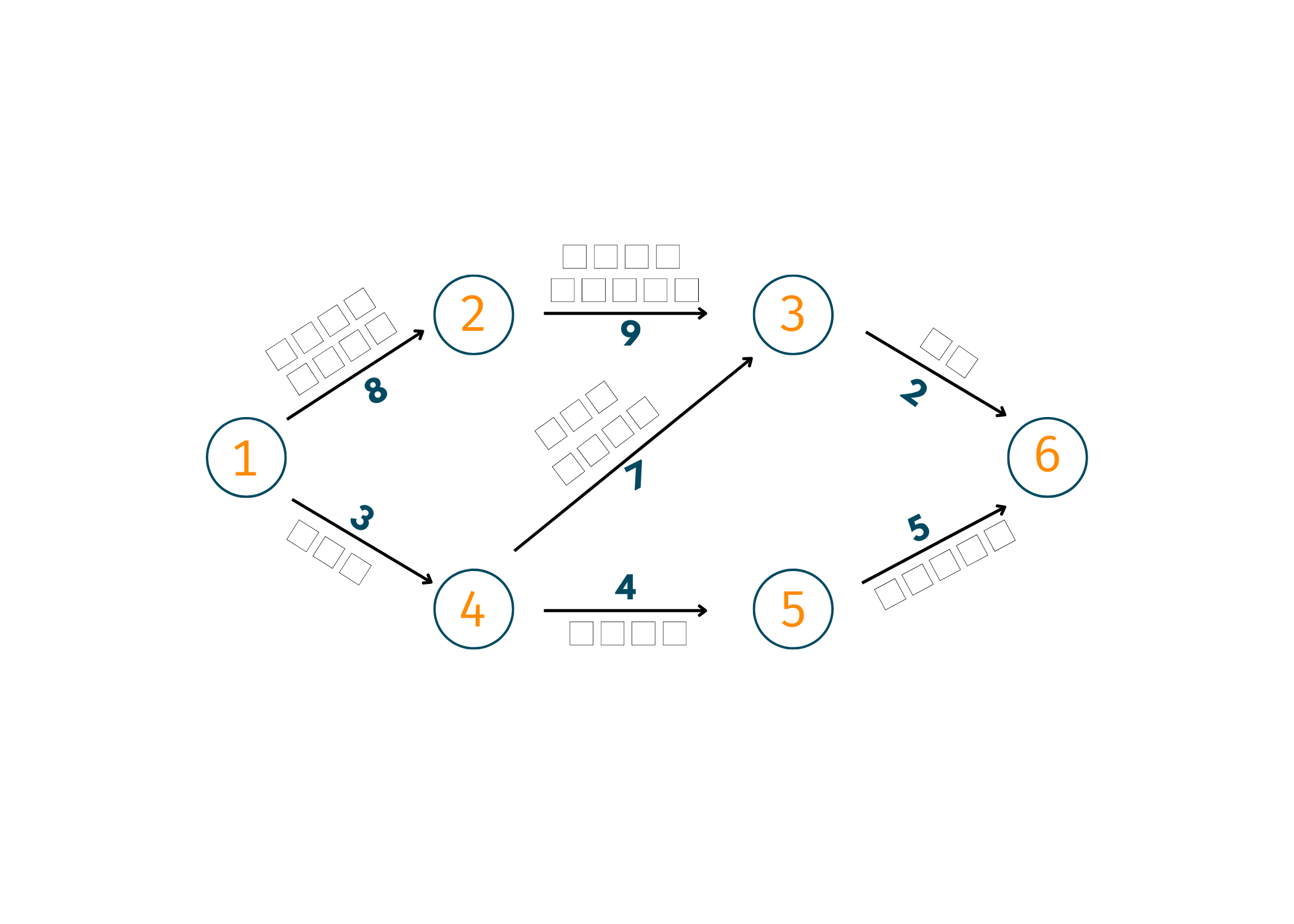
Below is the Java code for the Ford-Fulkerson algorithm:
// Ford-Fulkerson algorith in Java import java.util.LinkedList; class FordFulkerson { static final int Vertices = 6; // Using BFS as a searching algorithm boolean bfs(int Graph[][], int source, int dest, int p[]) { boolean visited[] = new boolean[Vertices]; for (int i = 0; i < Vertices; ++i) visited[i] = false; LinkedList<Integer> queue = new LinkedList<Integer>(); queue.add(source); visited[source] = true; p[source] = -1; while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v < Vertices; v++) { if (visited[v] == false && Graph[u][v] > 0) { queue.add(v); p[v] = u; visited[v] = true; } } } return (visited[dest] == true); } // Applying fordfulkerson algorithm int fordFulkerson(int graph[][], int source, int dest) { int u, v; int Graph[][] = new int[Vertices][Vertices]; for (u = 0; u < Vertices; u++) for (v = 0; v < Vertices; v++) Graph[u][v] = graph[u][v]; int p[] = new int[Vertices]; int max_flow = 0; //Updating the residual capacities of edges while (bfs(Graph, source, dest, p)) { int path_flow = Integer.MAX_VALUE; for (v = dest; v != source; v = p[v]) { u = p[v]; path_flow = Math.min(path_flow, Graph[u][v]); } for (v = dest; v != source; v = p[v]) { u = p[v]; Graph[u][v] -= path_flow; Graph[v][u] += path_flow; } // Adding the path flows max_flow += path_flow; } return max_flow; } public static void main(String[] args) { int graph[][] = new int[][] { { 0, 8, 0, 0, 3, 0 }, { 0, 0, 9, 0, 0, 0 }, { 0, 0, 0, 0, 7, 2 }, { 0, 0, 0, 0, 0, 5 }, { 0, 0, 7, 4, 0, 0 }, { 0, 0, 0, 0, 0, 0 } }; FordFulkerson m = new FordFulkerson(); System.out.println("Maximum Flow using Ford Fulkerson Algo: " + m.fordFulkerson(graph, 0, 5)); } }
Output:
Maximum Flow using Ford Fulkerson Algo: 6
The time taken by Ford Fulkerson Algorithm is O (max_flow * E).
Does Ford-Fulkerson Algorithm use BFS or DFS?
The Ford-Fulkerson algorithm can identify the augmenting path using either BFS (breadth-first search) or DFS (depth-first search). The properties of the graph and the technique used to determine the path influence the method selection.
If the graph is thin or there are fewer augmenting pathways, using DFS to locate them can produce a faster approach. BFS might be quicker, though, if the graph is thick or if there are many augmenting pathways.
In C++, the augmenting path can be found using either DFS or BFS. Here is an illustration of the Ford-Fulkerson algorithm implemented in C++ using DFS:
const int INF = 1e9; vector<vector<int>> residual; // residual graph vector<int> parent // DFS to find augmenting path Bool dfs(ints, int t){ vector <bool>visited (residual.sizw(), false); stack<int>stk; stk.push(s); visited[s] = true; parent[s] = -1; while (!stk.empty()) { int u = stk.top(); stk.pop(); for (int v = 0; v < residual.size(); v++) { if (!visited[v] && residual[u][v] > 0) { stk.push(v); parent[v] = u; visited[v] = true; if (v == t) { return true; } } } } return false; } // Ford-Fulkerson algorithm using DFS int maxFlow(int s, int t) { int max_flow = 0; while (dfs(s, t)) { int path_flow = INF; for (int v = t; v != s; v = parent[v]) { int u = parent[v]; path_flow = min(path_flow, residual[u][v]); } for (int v = t; v != s; v = parent[v]) { int u = parent[v]; residual[u][v] -= path_flow; residual[v][u] += path_flow; } max_flow += path_flow; } return max_flow; }
In this implementation, the 'residual vector represents the residual graph, and the 'parent' vector is used to store the parent node of each node in the augmenting path. The 'dfs' function performs a depth-first search to find an augmenting path in the residual graph, and the `maxFlow` function implements the Ford-Fulkerson algorithm using DFS.
To use BFS instead of DFS, we can replace the 'dfs' function with a BFS implementation, as follows:
bool bfs(int s, int t) { vector<bool> visited(residual.size(), false); queue<int> q; q.push(s); visited[s] = true; parent[s] = -1; while (!q.empty()) { int u = q.front(); q.pop(); for (int v = 0; v < residual.size(); v++) { if (!visited[v] && residual[u][v] > 0) { q.push(v); parent[v] = u; visited[v] = true; if (v == t) { return true; } } } } return false; }
In this approach, the stack is swapped out for a queue, and the augmenting path is discovered via a breadth-first search. The Ford-Fulkerson algorithm can be used using the maxFlow function and either DFS or BFS.
Conclusion
The Ford Fulkerson Algorithm is an essential topic to enhance your programming skills. While solving it a high sense of imagination power is definitely required to search for all the potential augmenting paths and find out the residual capacity of the same.