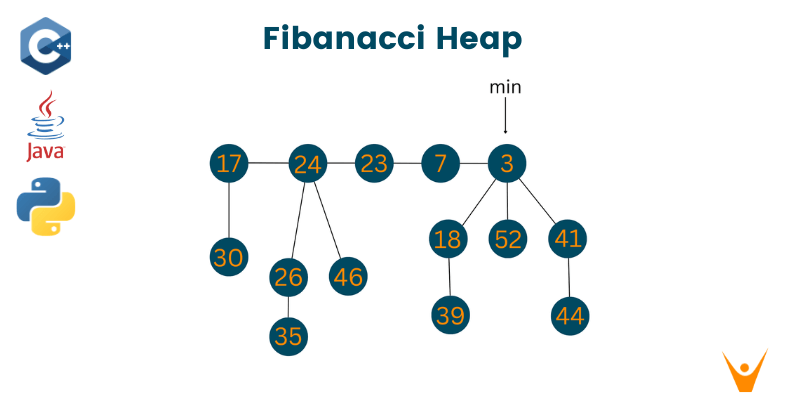
To become a successful software developer, the most important thing one should know is undoubtedly Data Structures & Algorithms. As you dive deeper into the topic, you'll find yourself in the never-ending ocean consisting of a humongous amount of questions about DSA. Although one should have a good understanding and practice of primary data structures, every once in a while, it never hurts to learn something new.
Fibonacci Heap is one such topic that every future developer should be well versed in, to gain a better job. When you hear the word Fibonacci, the first thought that comes to your head is the Fibonacci numbers. Well, those numbers do have their own importance, in this tech blog we shall primarily be discussing what is a Fibonacci Heap, various operations on the heap, its implementation, and time complexity.
So, let's dive into this deep ocean of knowledge and get ourselves some pearls of wisdom out of it!
What is a Fibonacci Heap?
A Fibonacci Heap is a particular implementation of the heap data structure that has a collection of trees and follows either min-heap or max-heap properties. These heaps are generally used to implement the elements of the priority queue in Dijkstra's algorithm. Using this heap in the specified algorithm provides an efficient running time for the program.
While dealing with the Fibonacci Heaps, a particular node can have either no children or more than two children. As compared to the binomial and binary heaps, this heap can undergo many operations efficiently.
Why is it called so?
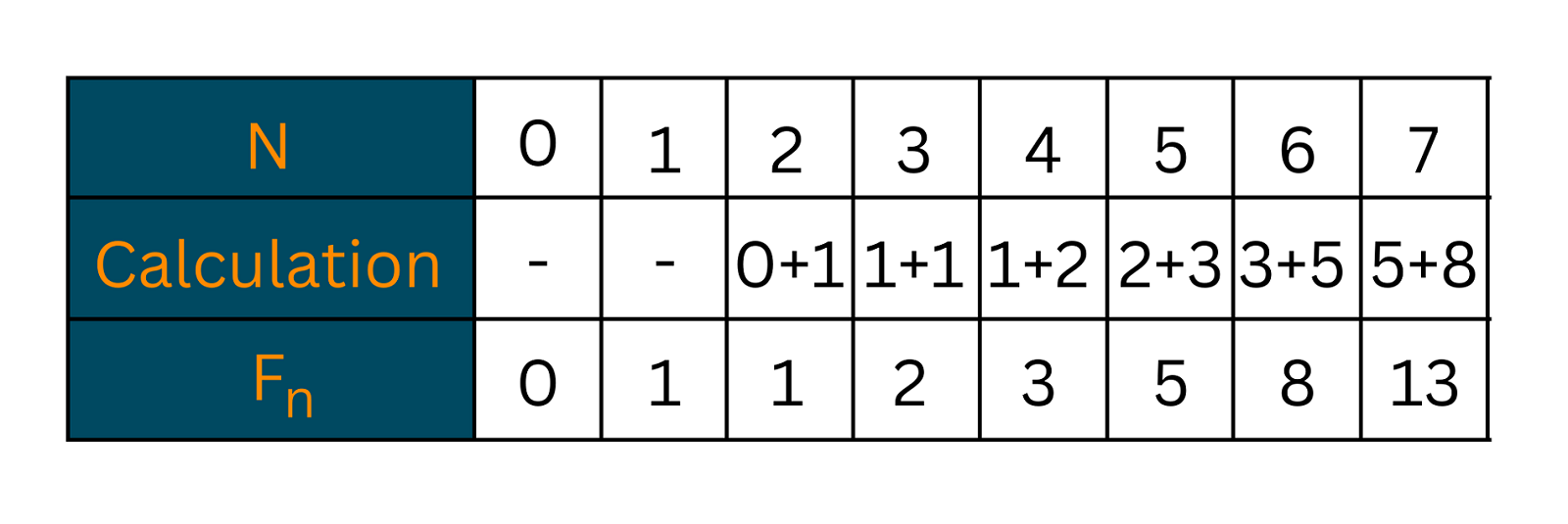
So, why this heap is called a Fibonacci Heap? The reason is that this heap uses the famous Fibonacci numbers in its structure. The main application of Fibonacci Heaps is that they improve the asymptotic execution time of Dijkstra's algorithm. Take a look at the illustration below to understand what Fibonacci Numbers are:
Properties of Fibonacci Heap
Just like other data structures, Fibonacci Heap also has its own unique properties/attributes. Some of them are listed below:
- The parent node is always smaller than the child (min-heap ordered tree).
- Trees within the heap are rooted but are unordered.
- This heap consists of a set of marked nodes.
- At the minimum element node, the pointer is maintained.
How does it work?
In the Fibonacci Heap, there is a pointer that keeps track of the minimum value in the heap. This smallest element is actually the root of the tree. All the tree roots in the heap are connected using the circular doubly linked list. This means that any node of the tree can be accessed by the pointer pointing toward the minimum value in the heap.
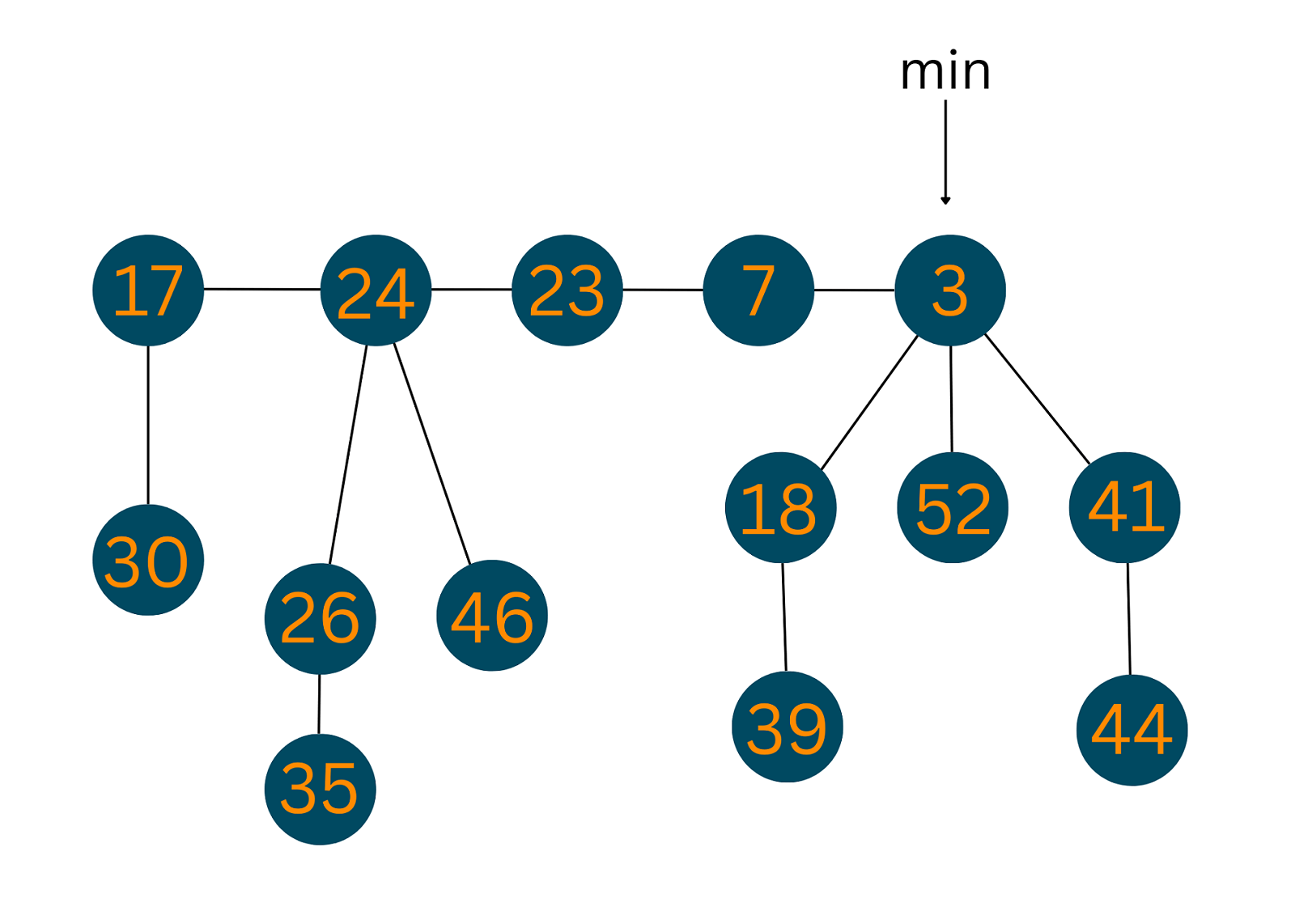
Operations on a Fibonacci Heap
A number of operations can be performed using a Fibonacci heap in comparatively less time as compared to other heaps. In this section, we shall be discussing the major operations of a Fibonacci Heap like insertion, deletion, merging, etc.
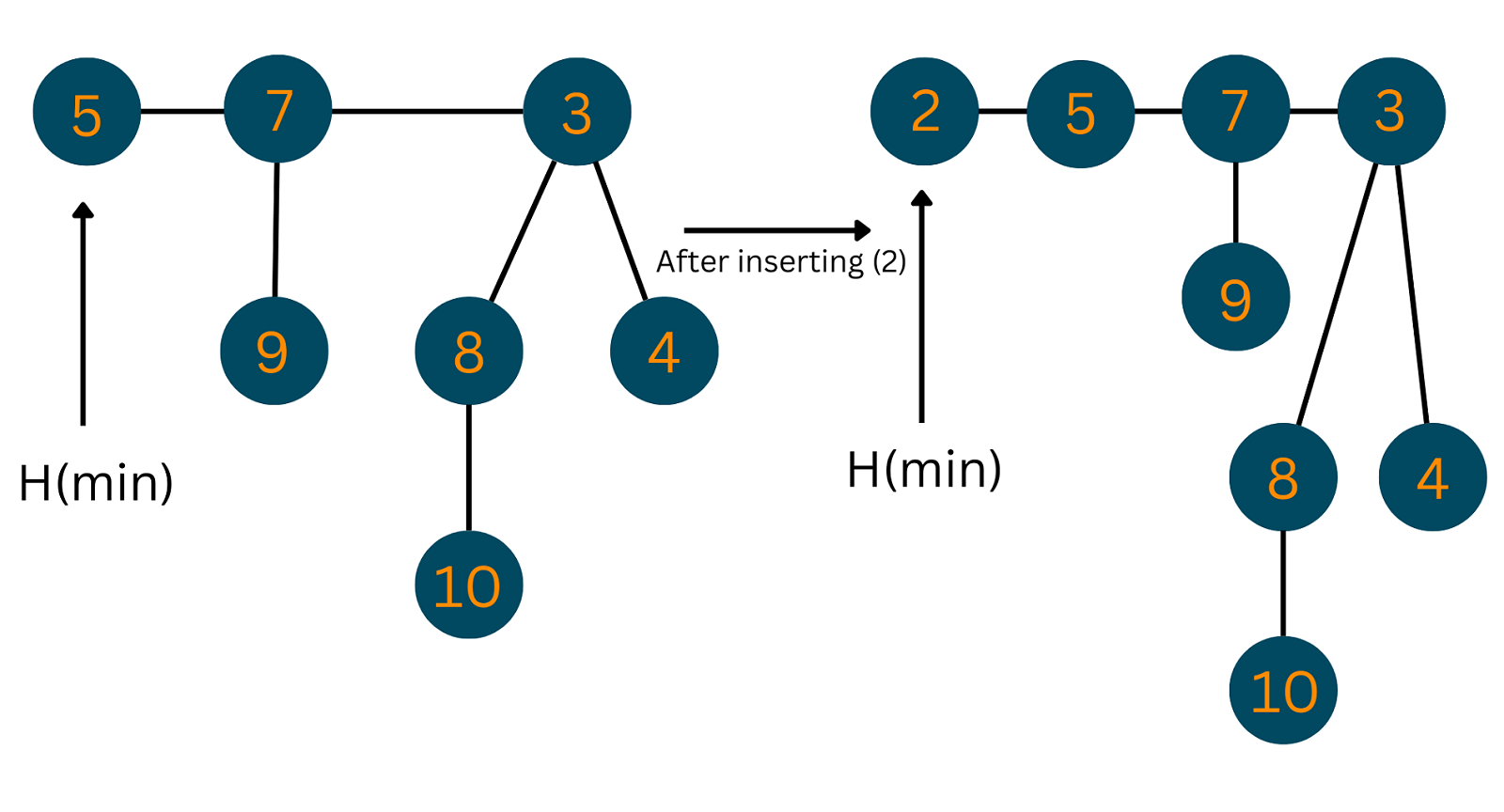
01) Insertion
To insert an element in a heap, follow the given algorithm:
1. Create a new node 'n'. 2. Find whether heap is empty or not 3. If(heap is empty) - make 'n' the only node - set the minimum pointer to 'n' 4. Else - insert 'n' into root list - update the value of minimum pointer
Take a look at the illustration below to understand what actually happened in the above steps:
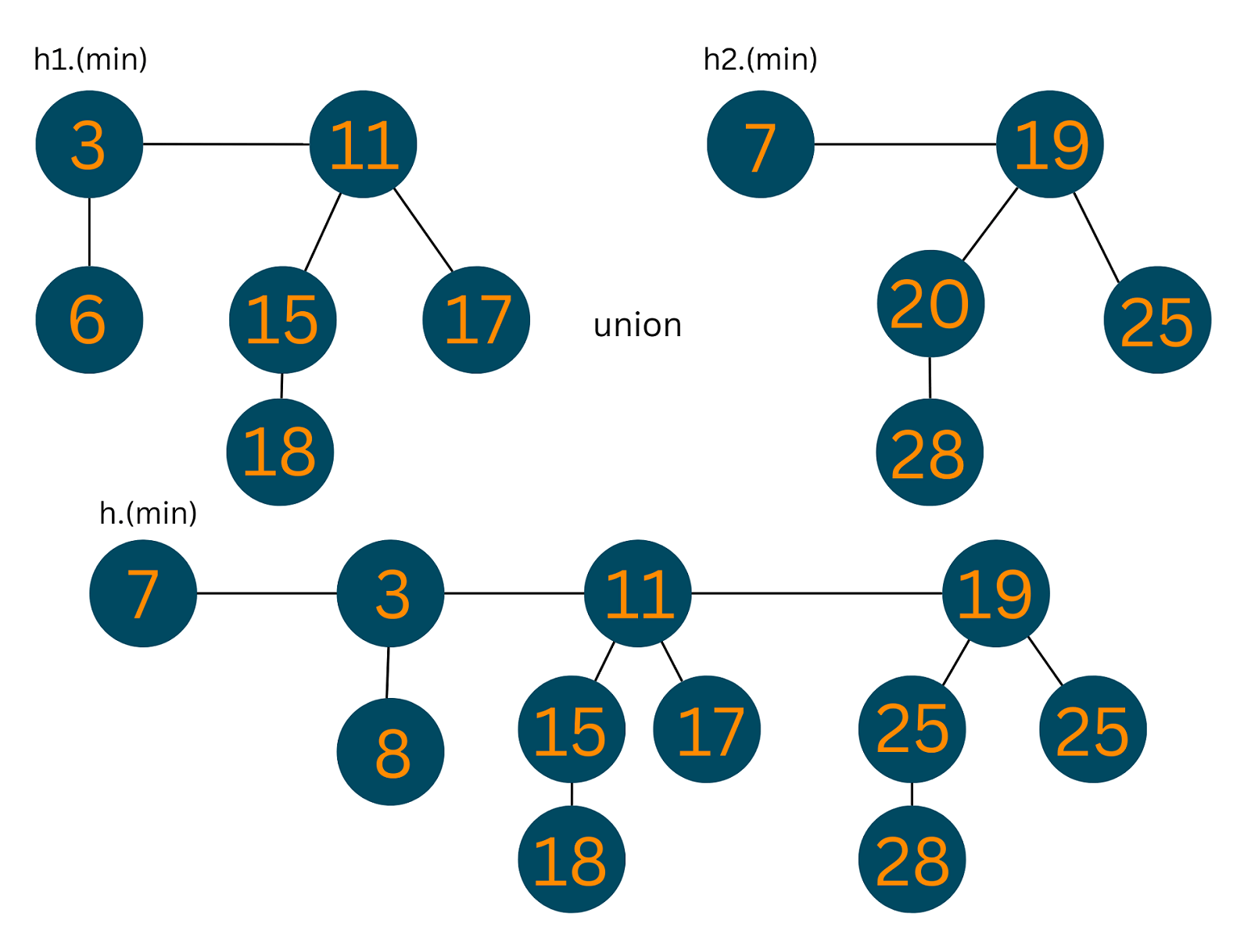
02) Union
For the union of 2 Fibonacci Heaps, the below steps need to be followed:
1. Join the root list of both heaps(h1, h2) and form a single Fibonacci Heap(h). 2. If h1(min) < h2(min) h(min) = h1(min) 3. Else h(min) = h2(min)
Take a look at the illustration below to understand what actually happened in the above steps:
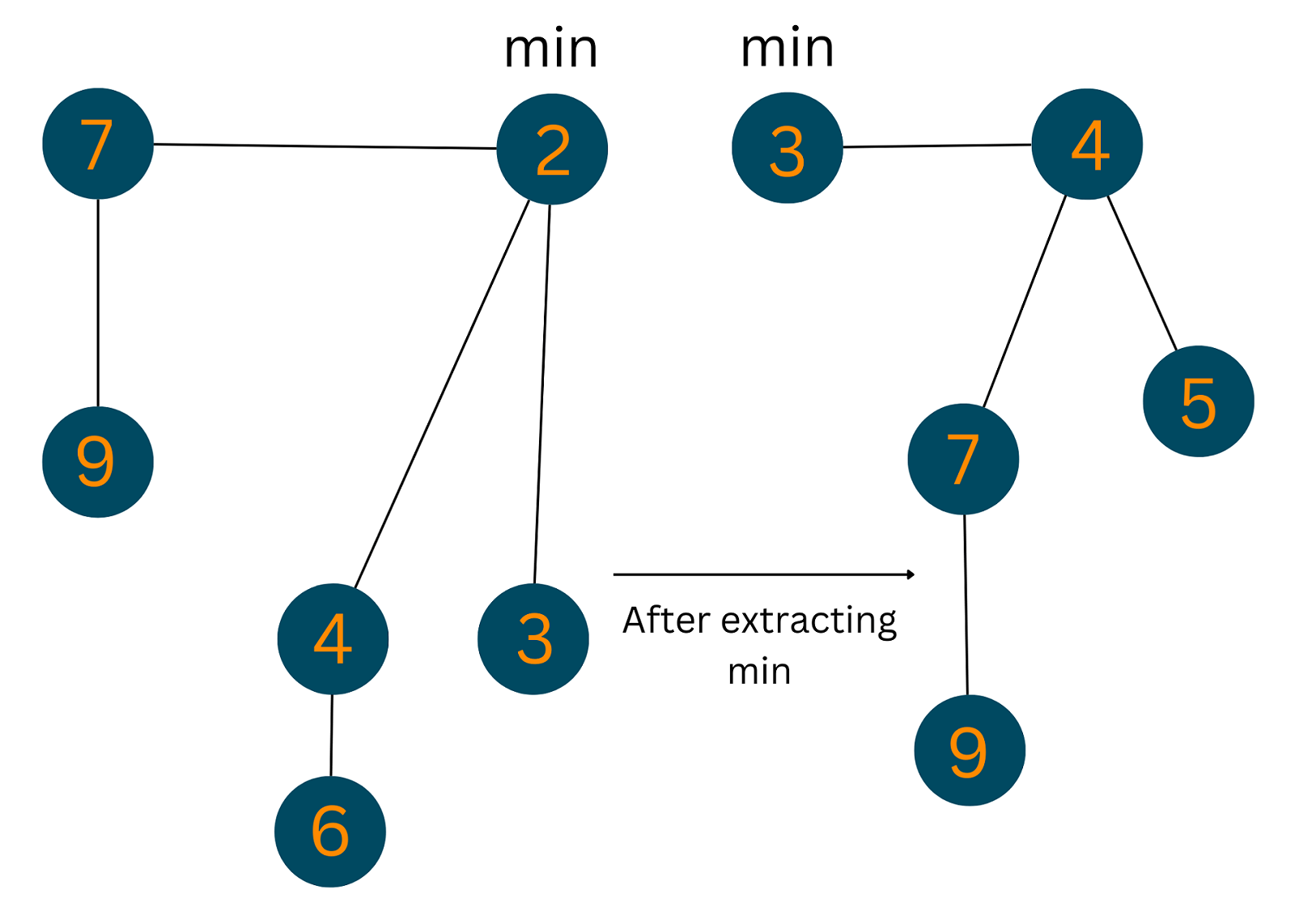
03) Extracting Min
This operation is used to find out the minimum element in the whole tree.
1. Delete the initial min node. 2. Set pointer to the next min node. 3. Add all the trees of the deleted node in the root list. 4. Create an array of degree pointers of the deleted node's size. 5. Set the current node as the degree pointer. 6. Move forward towards the next node. 7. If degrees are different -set degree pointer to the next node. 8. Else -join the Fibonacci trees by union operation. 9. Repeat steps 4 and 5 until the heap is completed.
Take a look at the illustration below to understand what actually happened in the above steps:
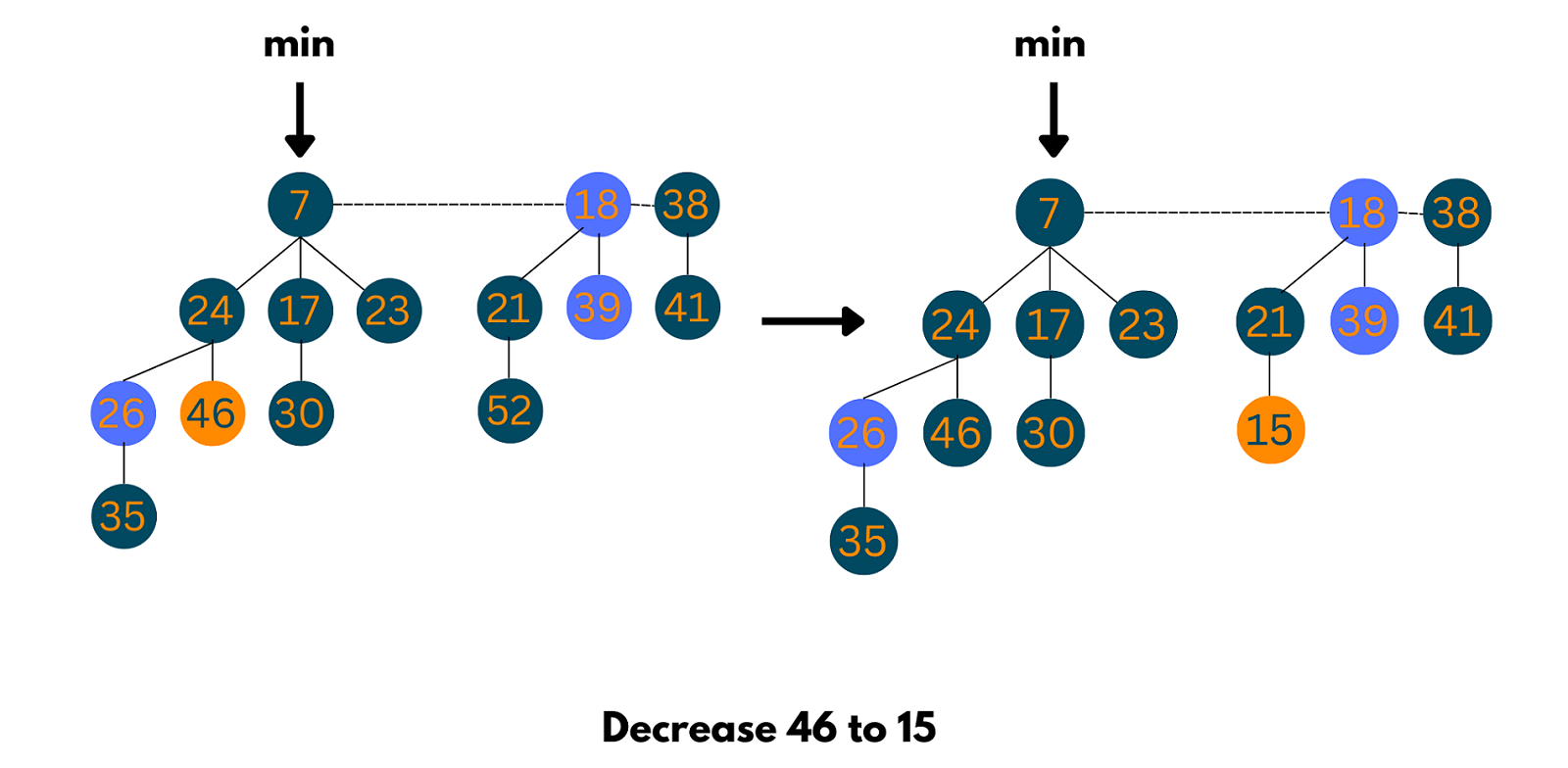
04) Decrease Key
This operation is used to decrease the value of a particular node to a lower value. Follow the steps to achieve the result:
1. Decrease the value of the node ‘x’ to the new value. 2. Case 1) If min-heap property is not violated: -Update min pointer 3. Case 2) If min-heap property is violated and parent of ‘x’ is not marked, -Cut off the link between ‘x’ and its parent. -Mark x's parent. -Add tree rooted at ‘x’ to the root list and update the min pointer 3. Case 3) If min-heap property is violated and parent of ‘x’ is marked: -Cut off the link between ‘x’ and its parent. -Add ‘x’ to the root list, updating min pointer -Cut off the link between p[x] and p[p[x]]. -Add p[x] to the root list, updating min pointer -If p[p[x]] is unmarked: -mark it. -Else: -cut off p[p[x]] and repeat steps taking p[p[x]] as ‘x’.
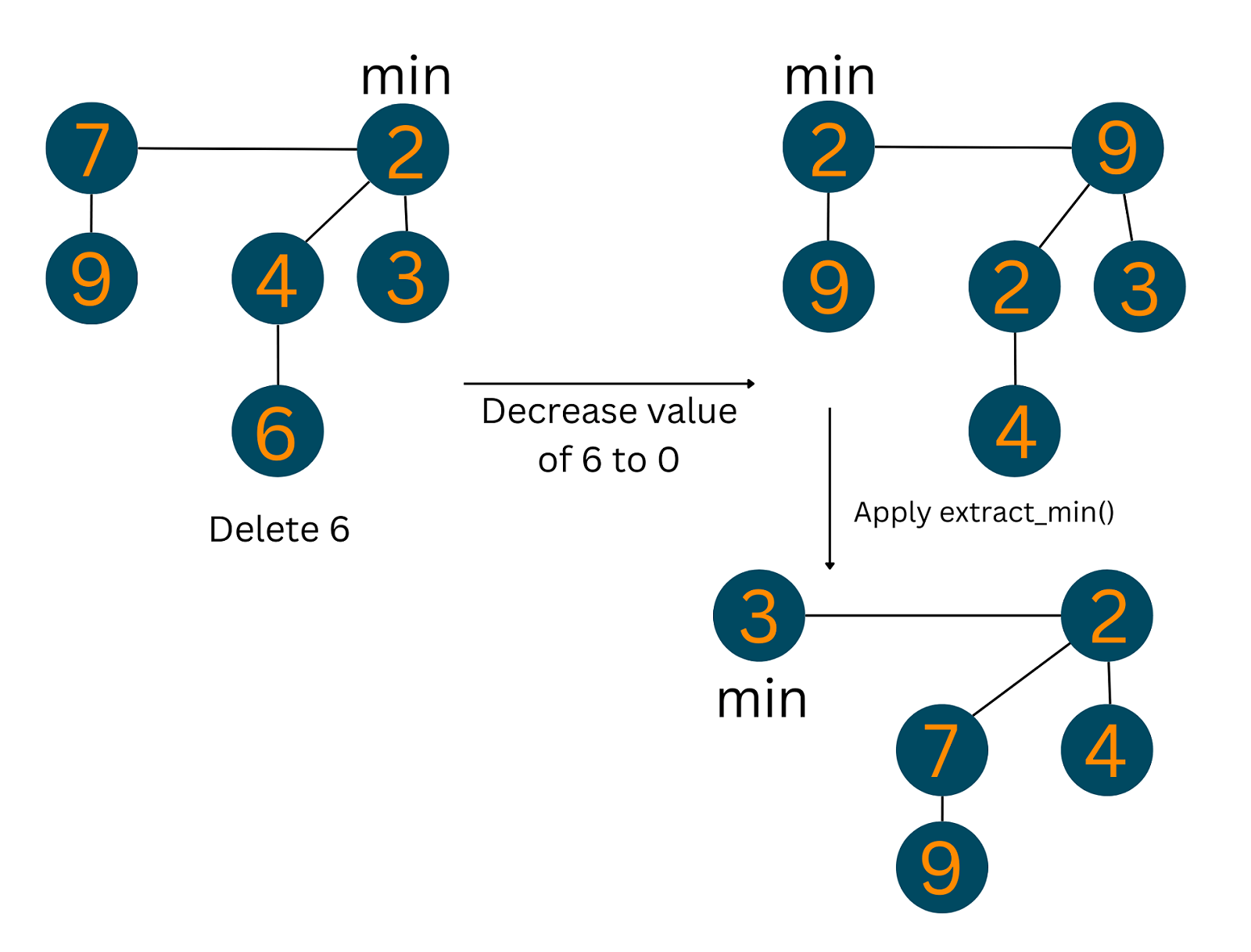
05) Deletion
1. Decrease the value of the node to be deleted ‘x’ to a minimum by using the previous Decrease_key() function. 2. Heapify the heap using min-heap property, bringing ‘x’ to the root list. 3. Apply Extract_min() algorithm to the Fibonacci heap.
Look at the below image to understand the output of the above operation:
Time Complexities of Fibonacci Heap Operations
The following table shows the time complexity for each operation on this heap:
| OPERATION | TIME COMPLEXITY |
| Insertion | O(1) |
| Find Min | O(1) |
| Union | O(1) |
| Extract Min | O(log n) |
| Decrease Key | O(1) |
| Delete Node | O(log n) |
C++ Implementation
Here is the C++ code to implement the Fibonacci heap:
#include #include #include using namespace std; // Creating a node
struct node { int n; int degree; node *parent; node *child; node *left; node *right; char mark; char C; }; // Implementing the Fibonacci heap class FibonacciHeap { private: int nH; node *H; //Declaring all the functions that are later to be used as operations on the heap public: node *InitializeHeap(); int Fibonnaci_link(node *, node *, node *); node *Create_node(int); node *Insert(node *, node *); node *Union(node *, node *); node *Extract_Min(node *); int Consolidate(node *); int Display(node *); node *Find(node *, int); int Decrease_key(node *, int, int); int Delete_key(node *, int); int Cut(node *, node *, node *); int Cascase_cut(node *, node *); FibonacciHeap() { H = InitializeHeap(); } }; // Initialize heap node *FibonacciHeap::InitializeHeap() { node *np; np = NULL; return np; } // Creating node node *FibonacciHeap::Create_node(int value) { node *x = new node; x->n = value; return x; } // Inserting node node *FibonacciHeap::Insert(node *H, node *x) { x->degree = 0; x->parent = NULL; x->child = NULL; x->left = x; x->right = x; x->mark = 'F'; x->C = 'N'; if (H != NULL) { (H->left)->right = x; x->right = H; x->left = H->left; H->left = x; if (x->n < H->n) H = x; } else { H = x; } nH = nH + 1; return H; } // Create linking int FibonacciHeap::Fibonnaci_link(node *H1, node *y, node *z) { (y->left)->right = y->right; (y->right)->left = y->left; if (z->right == z) H1 = z; y->left = y; y->right = y; y->parent = z; if (z->child == NULL) z->child = y; y->right = z->child; y->left = (z->child)->left; ((z->child)->left)->right = y; (z->child)->left = y; if (y->n < (z->child)->n) z->child = y; z->degree++; } // Union Operation node *FibonacciHeap::Union(node *H1, node *H2) { node *np; node *H = InitializeHeap(); H = H1; (H->left)->right = H2; (H2->left)->right = H; np = H->left; H->left = H2->left; H2->left = np; return H; } // Display the heap int FibonacciHeap::Display(node *H) { node *p = H; if (p == NULL) { cout << "Empty Heap" << endl; return 0; } cout << "Root Nodes: " << endl; do { cout << p->n; p = p->right; if (p != H) { cout << "-->"; } } while (p != H && p->right != NULL); cout << endl; } // Extract min node *FibonacciHeap::Extract_Min(node *H1) { node *p; node *ptr; node *z = H1; p = z; ptr = z; if (z == NULL) return z; node *x; node *np; x = NULL; if (z->child != NULL) x = z->child; if (x != NULL) { ptr = x; do { np = x->right; (H1->left)->right = x; x->right = H1; x->left = H1->left; H1->left = x; if (x->n < H1->n) H1 = x; x->parent = NULL; x = np; } while (np != ptr); } (z->left)->right = z->right; (z->right)->left = z->left; H1 = z->right; if (z == z->right && z->child == NULL) H = NULL; else { H1 = z->right; Consolidate(H1); } nH = nH - 1; return p; } // Consolidation Function int FibonacciHeap::Consolidate(node *H1) { int d, i; float f = (log(nH)) / (log(2)); int D = f; node *A[D]; for (i = 0; i <= D; i++) A[i] = NULL; node *x = H1; node *y; node *np; node *pt = x; do { pt = pt->right; d = x->degree; while (A[d] != NULL) { y = A[d]; if (x->n > y->n) { np = x; x = y; y = np; } if (y == H1) H1 = x; Fibonnaci_link(H1, y, x); if (x->right == x) H1 = x; A[d] = NULL; d = d + 1; } A[d] = x; x = x->right; } while (x != H1); H = NULL; for (int j = 0; j <= D; j++) { if (A[j] != NULL) { A[j]->left = A[j]; A[j]->right = A[j]; if (H != NULL) { (H->left)->right = A[j]; A[j]->right = H; A[j]->left = H->left; H->left = A[j]; if (A[j]->n < H->n) H = A[j]; } else { H = A[j]; } if (H == NULL) H = A[j]; else if (A[j]->n < H->n) H = A[j]; } } } // Decrease Key Operation int FibonacciHeap::Decrease_key(node *H1, int x, int k) { node *y; if (H1 == NULL) { cout << "The Heap is Empty" << endl; return 0; } node *ptr = Find(H1, x); if (ptr == NULL) { cout << "Node not found in the Heap" << endl; return 1; } if (ptr->n < k) { cout << "Entered key greater than current key" << endl; return 0; } ptr->n = k; y = ptr->parent; if (y != NULL && ptr->n < y->n) { Cut(H1, ptr, y); Cascase_cut(H1, y); } if (ptr->n < H->n) H = ptr; return 0; } // Cutting Function int FibonacciHeap::Cut(node *H1, node *x, node *y) { if (x == x->right) y->child = NULL; (x->left)->right = x->right; (x->right)->left = x->left; if (x == y->child) y->child = x->right; y->degree = y->degree - 1; x->right = x; x->left = x; (H1->left)->right = x; x->right = H1; x->left = H1->left; H1->left = x; x->parent = NULL; x->mark = 'F'; } // Cascade cut int FibonacciHeap::Cascase_cut(node *H1, node *y) { node *z = y->parent; if (z != NULL) { if (y->mark == 'F') { y->mark = 'T'; } else { Cut(H1, y, z); Cascase_cut(H1, z); } } } // Search function node *FibonacciHeap::Find(node *H, int k) { node *x = H; x->C = 'Y'; node *p = NULL; if (x->n == k) { p = x; x->C = 'N'; return p; } if (p == NULL) { if (x->child != NULL) p = Find(x->child, k); if ((x->right)->C != 'Y') p = Find(x->right, k); } x->C = 'N'; return p; } // Deleting key int FibonacciHeap::Delete_key(node *H1, int k) { node *np = NULL; int t; t = Decrease_key(H1, k, -5000); if (!t) np = Extract_Min(H); if (np != NULL) cout << "Key Deleted" << endl; else cout << "Key not Deleted" << endl; return 0; } int main() { int n, m, l; FibonacciHeap fh; node *p; node *H; H = fh.InitializeHeap(); p = fh.Create_node(7); H = fh.Insert(H, p); p = fh.Create_node(3); H = fh.Insert(H, p); p = fh.Create_node(17); H = fh.Insert(H, p); p = fh.Create_node(24); H = fh.Insert(H, p); fh.Display(H); p = fh.Extract_Min(H); if (p != NULL) cout << "The node with minimum key: " << p->n << endl; else cout << "Heap is empty" << endl; m = 26; l = 16; fh.Decrease_key(H, m, l); m = 16; fh.Delete_key(H, m); }
Java Implementation
Here is the Java code to implement the Fibonacci heap:
// Operations on Fibonacci Heap in Java // Node creation class node { node parent; node left; node right; node child; int degree; boolean mark; int key; public node() { this.degree = 0; this.mark = false; this.parent = null; this.left = this; this.right = this; this.child = null; this.key = Integer.MAX_VALUE; } node(int x) { this(); this.key = x; } void set_parent(node x) { this.parent = x; } node get_parent() { return this.parent; } void set_left(node x) { this.left = x; } node get_left() { return this.left; } void set_right(node x) { this.right = x; } node get_right() { return this.right; } void set_child(node x) { this.child = x; } node get_child() { return this.child; } void set_degree(int x) { this.degree = x; } int get_degree() { return this.degree; } void set_mark(boolean m) { this.mark = m; } boolean get_mark() { return this.mark; } void set_key(int x) { this.key = x; } int get_key() { return this.key; } } public class fibHeap { node min; int n; boolean trace; node found; public boolean get_trace() { return trace; } public void set_trace(boolean t) { this.trace = t; } public static fibHeap create_heap() { return new fibHeap(); } fibHeap() { min = null; n = 0; trace = false; } private void insert(node x) { if (min == null) { min = x; x.set_left(min); x.set_right(min); } else { x.set_right(min); x.set_left(min.get_left()); min.get_left().set_right(x); min.set_left(x); if (x.get_key() < min.get_key()) min = x; } n += 1; } public void insert(int key) { insert(new node(key)); } public void display() { display(min); System.out.println(); } private void display(node c) { System.out.print("("); if (c == null) { System.out.print(")"); return; } else { node temp = c; do { System.out.print(temp.get_key()); node k = temp.get_child(); display(k); System.out.print("->"); temp = temp.get_right(); } while (temp != c); System.out.print(")"); } } public static void merge_heap(fibHeap H1, fibHeap H2, fibHeap H3) { H3.min = H1.min; if (H1.min != null && H2.min != null) { node t1 = H1.min.get_left(); node t2 = H2.min.get_left(); H1.min.set_left(t2); t1.set_right(H2.min); H2.min.set_left(t1); t2.set_right(H1.min); } if (H1.min == null || (H2.min != null && H2.min.get_key() < H1.min.get_key())) H3.min = H2.min; H3.n = H1.n + H2.n; } public int find_min() { return this.min.get_key(); } private void display_node(node z) { System.out.println("right: " + ((z.get_right() == null) ? "-1" : z.get_right().get_key())); System.out.println("left: " + ((z.get_left() == null) ? "-1" : z.get_left().get_key())); System.out.println("child: " + ((z.get_child() == null) ? "-1" : z.get_child().get_key())); System.out.println("degree " + z.get_degree()); } public int extract_min() { node z = this.min; if (z != null) { node c = z.get_child(); node k = c, p; if (c != null) { do { p = c.get_right(); insert(c); c.set_parent(null); c = p; } while (c != null && c != k); } z.get_left().set_right(z.get_right()); z.get_right().set_left(z.get_left()); z.set_child(null); if (z == z.get_right()) this.min = null; else { this.min = z.get_right(); this.consolidate(); } this.n -= 1; return z.get_key(); } return Integer.MAX_VALUE; } public void consolidate() { double phi = (1 + Math.sqrt(5)) / 2; int Dofn = (int) (Math.log(this.n) / Math.log(phi)); node[] A = new node[Dofn + 1]; for (int i = 0; i <= Dofn; ++i) A[i] = null; node w = min; if (w != null) { node check = min; do { node x = w; int d = x.get_degree(); while (A[d] != null) { node y = A[d]; if (x.get_key() > y.get_key()) { node temp = x; x = y; y = temp; w = x; } fib_heap_link(y, x); check = x; A[d] = null; d += 1; } A[d] = x; w = w.get_right(); } while (w != null && w != check); this.min = null; for (int i = 0; i <= Dofn; ++i) { if (A[i] != null) { insert(A[i]); } } } } // Linking operation private void fib_heap_link(node y, node x) { y.get_left().set_right(y.get_right()); y.get_right().set_left(y.get_left()); node p = x.get_child(); if (p == null) { y.set_right(y); y.set_left(y); } else { y.set_right(p); y.set_left(p.get_left()); p.get_left().set_right(y); p.set_left(y); } y.set_parent(x); x.set_child(y); x.set_degree(x.get_degree() + 1); y.set_mark(false); } // Search operation private void find(int key, node c) { if (found != null || c == null) return; else { node temp = c; do { if (key == temp.get_key()) found = temp; else { node k = temp.get_child(); find(key, k); temp = temp.get_right(); } } while (temp != c && found == null); } } public node find(int k) { found = null; find(k, this.min); return found; } public void decrease_key(int key, int nval) { node x = find(key); decrease_key(x, nval); } // Decrease key operation private void decrease_key(node x, int k) { if (k > x.get_key()) return; x.set_key(k); node y = x.get_parent(); if (y != null && x.get_key() < y.get_key()) { cut(x, y); cascading_cut(y); } if (x.get_key() < min.get_key()) min = x; } // Cut operation private void cut(node x, node y) { x.get_right().set_left(x.get_left()); x.get_left().set_right(x.get_right()); y.set_degree(y.get_degree() - 1); x.set_right(null); x.set_left(null); insert(x); x.set_parent(null); x.set_mark(false); } private void cascading_cut(node y) { node z = y.get_parent(); if (z != null) { if (y.get_mark() == false) y.set_mark(true); else { cut(y, z); cascading_cut(z); } } } // Delete operations public void delete(node x) { decrease_key(x, Integer.MIN_VALUE); int p = extract_min(); } public static void main(String[] args) { fibHeap obj = create_heap(); obj.insert(7); obj.insert(26); obj.insert(30); obj.insert(39); obj.insert(10); obj.display(); System.out.println(obj.extract_min()); obj.display(); System.out.println(obj.extract_min()); obj.display(); System.out.println(obj.extract_min()); obj.display(); System.out.println(obj.extract_min()); obj.display(); System.out.println(obj.extract_min()); obj.display(); } }
Python Implementation
Here is the Python code to implement the Fibonacci heap:
# Fibonacci Heap in python import math # Creating fibonacci tree class FibonacciTree: def __init__(self, value): self.value = value self.child = [] self.order = 0 # Adding tree at the end of the tree def add_at_end(self, t): self.child.append(t) self.order = self.order + 1 # Creating Fibonacci heap class FibonacciHeap: def __init__(self): self.trees = [] self.least = None self.count = 0 # Insert a node def insert_node(self, value): new_tree = FibonacciTree(value) self.trees.append(new_tree) if (self.least is None or value < self.least.value): self.least = new_tree self.count = self.count + 1 # Get minimum value def get_min(self): if self.least is None: return None return self.least.value # Extract the minimum value def extract_min(self): smallest = self.least if smallest is not None: for child in smallest.child: self.trees.append(child) self.trees.remove(smallest) if self.trees == []: self.least = None else: self.least = self.trees[0] self.consolidate() self.count = self.count - 1 return smallest.value # Consolidate the tree def consolidate(self): aux = (floor_log(self.count) + 1) * [None] while self.trees != []: x = self.trees[0] order = x.order self.trees.remove(x) while aux[order] is not None: y = aux[order] if x.value > y.value: x, y = y, x x.add_at_end(y) aux[order] = None order = order + 1 aux[order] = x self.least = None for k in aux: if k is not None: self.trees.append(k) if (self.least is None or k.value < self.least.value): self.least = k def floor_log(x): return math.frexp(x)[1] - 1 fibonacci_heap = FibonacciHeap() fibonacci_heap.insert_node(7) fibonacci_heap.insert_node(3) fibonacci_heap.insert_node(17) fibonacci_heap.insert_node(24) print('the minimum value of the fibonacci heap: {}'.format(fibonacci_heap.get_min())) print('the minimum value removed: {}'.format(fibonacci_heap.extract_min()))
Is Fibonacci Heap faster than Binary Heap?
To answer the above question, we have provided a table for you to compare the time complexities of different operations on both heaps. So, find it out yourself!
| Operation | Binary Heap | Fibonacci Heap |
| insert | O(log N) | O(1) |
| find-min | O(1) | O(1) |
| delete | O(log N) | O(log N) |
| decrease-key | O(log N) | O(1) |
| union | O(N) | O(1) |
So, after looking carefully through the table, we are pretty sure you must have understood which heap is better.
Conclusion
Fibonacci Heaps are undoubtedly an important part to prepare for your placements as they play a vital role in distance-finding algorithms like Djikstra's and Prims. So, in today's tech blog we discussed all information about Fibonacci Heaps, their properties, various operations on them, and most importantly a comparison with Binary Heap.