Logistic Regression is a classifier that belongs to the class of linear models. Mathematically, it is a sigmoid transformation of the fitted equation of a line (in n-dimensions where n is the number of features taken into account) that denotes the class probabilities absolutely suitable for Binary Classification after a proper thresholding is done. This line is known as Decision Boundary which is a boundary line created by the classifier (here, Logistic Regression) to signify the decision regions. The visualization of decision boundary along with the data-points (colored data-points to describe the respective labeled classes) is difficult if the data is more than 2-3 dimensions. In this article, Decision Boundary Visualization is performed by training a Logistic Regression Model on the Breast Cancer Wisconsin (Diagnostic) Data Set after applying Principal Component Analysis on the same in order to reduce the number of dimensions of the dataset to 2 dimensions.
15 Steps to Generate Decision Boundary Visualization
1. Importing necessary libraries
# importing necessary libraries import numpy as np import pandas as pd pd.set_option("display.max_rows", None, "display.max_columns", None) # displaying all rows and columns of a dataframe from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.decomposition import IncrementalPCA from sklearn.model_selection import GridSearchCV from sklearn.linear_model import LogisticRegression from sklearn import metrics import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline
2. Reading the Breast Cancer Wisconsin (Diagnostic) Dataset
The Breast Cancer Wisconsin (Diagnostic) Dataset is obtained from Kaggle (https://www.kaggle.com/uciml/breast-cancer-wisconsin-data) and is originally available at the UCI Data Repository.
# reading the Breast Cancer Wisconsin (Diagnostic) Data Set df = pd.read_csv('data.csv') # displaying top 5 instances of the dataset print(df.head())
Corresponding Output
id diagnosis radius_mean texture_mean perimeter_mean area_mean \ 0 842302 M 17.99 10.38 122.80 1001.0 1 842517 M 20.57 17.77 132.90 1326.0 2 84300903 M 19.69 21.25 130.00 1203.0 3 84348301 M 11.42 20.38 77.58 386.1 4 84358402 M 20.29 14.34 135.10 1297.0 smoothness_mean compactness_mean concavity_mean concave points_mean \ 0 0.11840 0.27760 0.3001 0.14710 1 0.08474 0.07864 0.0869 0.07017 2 0.10960 0.15990 0.1974 0.12790 3 0.14250 0.28390 0.2414 0.10520 4 0.10030 0.13280 0.1980 0.10430 symmetry_mean fractal_dimension_mean radius_se texture_se perimeter_se \ 0 0.2419 0.07871 1.0950 0.9053 8.589 1 0.1812 0.05667 0.5435 0.7339 3.398 2 0.2069 0.05999 0.7456 0.7869 4.585 3 0.2597 0.09744 0.4956 1.1560 3.445 4 0.1809 0.05883 0.7572 0.7813 5.438 area_se smoothness_se compactness_se concavity_se concave points_se \ 0 153.40 0.006399 0.04904 0.05373 0.01587 1 74.08 0.005225 0.01308 0.01860 0.01340 2 94.03 0.006150 0.04006 0.03832 0.02058 3 27.23 0.009110 0.07458 0.05661 0.01867 4 94.44 0.011490 0.02461 0.05688 0.01885 symmetry_se fractal_dimension_se radius_worst texture_worst \ 0 0.03003 0.006193 25.38 17.33 1 0.01389 0.003532 24.99 23.41 2 0.02250 0.004571 23.57 25.53 3 0.05963 0.009208 14.91 26.50 4 0.01756 0.005115 22.54 16.67 perimeter_worst area_worst smoothness_worst compactness_worst \ 0 184.60 2019.0 0.1622 0.6656 1 158.80 1956.0 0.1238 0.1866 2 152.50 1709.0 0.1444 0.4245 3 98.87 567.7 0.2098 0.8663 4 152.20 1575.0 0.1374 0.2050 concavity_worst concave points_worst symmetry_worst \ 0 0.7119 0.2654 0.4601 1 0.2416 0.1860 0.2750 2 0.4504 0.2430 0.3613 3 0.6869 0.2575 0.6638 4 0.4000 0.1625 0.2364 fractal_dimension_worst Unnamed: 32 0 0.11890 NaN 1 0.08902 NaN 2 0.08758 NaN 3 0.17300 NaN 4 0.07678 NaN
3. Dropping unwanted columns, 'id' and 'Unnamed: 32' are dropped
# the unwanted columns, 'id' and 'Unnamed: 32' are dropped df.drop(['id', 'Unnamed: 32'], axis = 1, inplace = True)
4. Label Encoding of the Target Variable
# label-encoding of the target label, 'diagnosis' such that B(Benign) -> 0 and M (Malignant) -> 1 df['diagnosis'] = df['diagnosis'].map({'B':0, 'M':1})
5. Creating the Feature Set and Target Label variables
# spliting into X (features) and y (target label) X = df.iloc[:, 1:] y = df['diagnosis']
6. 80-20 splitting the dataset into Training Set and Test Set
# 80-20 splitting into train and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = 0.8, test_size = 0.2, random_state = 1234)
7. Feature Scaling of the features in the Training and Test Set
# feature scaling of the features in Training and Test Set columns = X_train.columns scalerx = StandardScaler() X_train_scaled = scalerx.fit_transform(X_train) X_train_scaled = pd.DataFrame(X_train_scaled, columns = columns) X_test_scaled = scalerx.transform(X_test) X_test_scaled = pd.DataFrame(X_test_scaled, columns = columns)
8. Principal Component Analysis (PCA) to reduce the dimensionality of the data into 2 dimensions in both Training and Test Set
# Incremental Principal Component Analysis to select 2 features such that they explain as much variance as possible pca = IncrementalPCA(n_components = 2) X_train_pca = pca.fit_transform(X_train_scaled) X_test_pca = pca.transform(X_test_scaled)
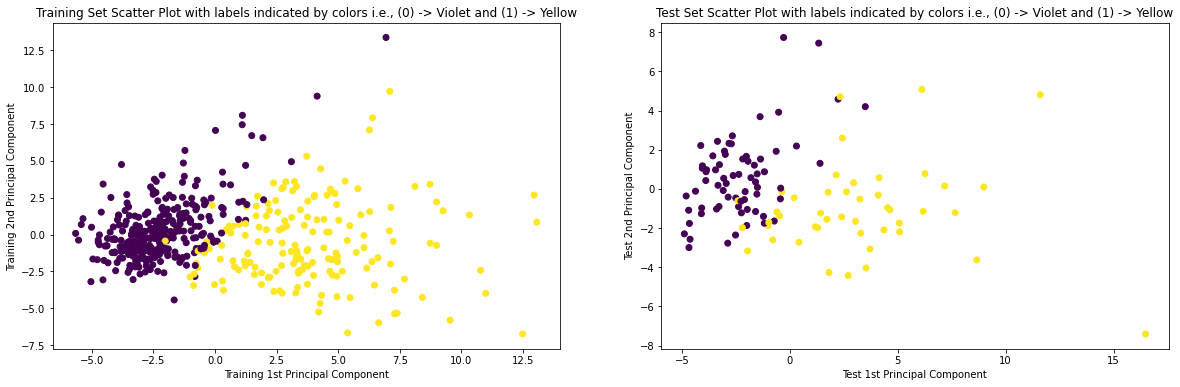
9. Plotting the Scatter-Plot of Training and Test Set
# Scatter Plot of Training and Test Set with labels indicated by colors plt.figure(figsize = (20, 6)) plt.subplot(1, 2, 1) plt.scatter(X_train_pca[:,0], X_train_pca[:,1], c = y_train) plt.xlabel('Training 1st Principal Component') plt.ylabel('Training 2nd Principal Component') plt.title('Training Set Scatter Plot with labels indicated by colors i.e., (0) -> Violet and (1) -> Yellow') plt.subplot(1, 2, 2) plt.scatter(X_test_pca[:,0], X_test_pca[:,1], c = y_test) plt.xlabel('Test 1st Principal Component') plt.ylabel('Test 2nd Principal Component') plt.title('Test Set Scatter Plot with labels indicated by colors i.e., (0) -> Violet and (1) -> Yellow') plt.show()
Corresponding Output
10. Performing 5-Fold Grid-Search Cross Validation on Logistic Regression Classifier on the Training Set
# 5-Fold Grid-Search Cross Validation on Logistic Regression Classifier for tuning the hyper-parameter, C with Accuracy scoring params = {'C':[0.01, 0.1, 1, 10, 100]} clf = LogisticRegression() folds = 5 model_cv = GridSearchCV(estimator = clf, param_grid = params, scoring= 'accuracy', cv = folds, return_train_score=True, verbose = 3) model_cv.fit(X_train_pca, y_train)
Corresponding Output
Fitting 5 folds for each of 5 candidates, totalling 25 fits [CV 1/5] END .........................................C=0.01; total time= 0.0s [CV 2/5] END .........................................C=0.01; total time= 0.0s [CV 3/5] END .........................................C=0.01; total time= 0.0s [CV 4/5] END .........................................C=0.01; total time= 0.0s [CV 5/5] END .........................................C=0.01; total time= 0.0s [CV 1/5] END ..........................................C=0.1; total time= 0.0s [CV 2/5] END ..........................................C=0.1; total time= 0.0s [CV 3/5] END ..........................................C=0.1; total time= 0.0s [CV 4/5] END ..........................................C=0.1; total time= 0.0s [CV 5/5] END ..........................................C=0.1; total time= 0.0s [CV 1/5] END ............................................C=1; total time= 0.0s [CV 2/5] END ............................................C=1; total time= 0.0s [CV 3/5] END ............................................C=1; total time= 0.0s [CV 4/5] END ............................................C=1; total time= 0.0s [CV 5/5] END ............................................C=1; total time= 0.0s [CV 1/5] END ...........................................C=10; total time= 0.0s [CV 2/5] END ...........................................C=10; total time= 0.0s [CV 3/5] END ...........................................C=10; total time= 0.0s [CV 4/5] END ...........................................C=10; total time= 0.0s [CV 5/5] END ...........................................C=10; total time= 0.0s [CV 1/5] END ..........................................C=100; total time= 0.0s [CV 2/5] END ..........................................C=100; total time= 0.0s [CV 3/5] END ..........................................C=100; total time= 0.0s [CV 4/5] END ..........................................C=100; total time= 0.0s [CV 5/5] END ..........................................C=100; total time= 0.0s GridSearchCV(cv=5, estimator=LogisticRegression(), param_grid={'C': [0.01, 0.1, 1, 10, 100]}, return_train_score=True, scoring='accuracy', verbose=3)
11. Getting the Best Hyper-parameter from the Grid-Search performed above
# getting the best hyper-parameter print(model_cv.best_params_)
Corresponding Output
{'C': 10}
12. Re-training the Logistic Regression Classifier with the best hyper-parameter, C = 10 (obtained above)
# re-training the Logistic Regression Classifier with the best hyper-parameter, C = 10 model = LogisticRegression(C = 10).fit(X_train_pca, y_train)
13. Obtaining the Training Set and Test Set Predictions given by the model, trained in the last step
# getting the Training Set Predictions y_train_pred = model.predict(X_train_pca) # getting the Test Set Predictions y_test_pred = model.predict(X_test_pca)
14. Performance Analysis of the Logistic Regression Model in terms of Accuracy, Precision, Recall and F1-Score
# Getting the Training and Test Accuracy of the Logistic Regression Model print('Training Accuracy of the Model: ', metrics.accuracy_score(y_train, y_train_pred)) print('Test Accuracy of the Model: ', metrics.accuracy_score(y_test, y_test_pred)) print() # Getting the Training and Test Precision of the Logistic Regression Model print('Training Precision of the Model: ', metrics.precision_score(y_train, y_train_pred)) print('Test Precision of the Model: ', metrics.precision_score(y_test, y_test_pred)) print() # Getting the Training and Test Recall of the Logistic Regression Model print('Training Recall of the Model: ', metrics.recall_score(y_train, y_train_pred)) print('Test Recall of the Model: ', metrics.recall_score(y_test, y_test_pred)) print() # Getting the Training and Test F1-Score of the Logistic Regression Model print('Training F1-Score of the Model: ', metrics.f1_score(y_train, y_train_pred)) print('Test F1-Score of the Model: ', metrics.f1_score(y_test, y_test_pred)) print()
Corresponding Output
Training Accuracy of the Model: 0.9648351648351648 Test Accuracy of the Model: 0.9035087719298246 Training Precision of the Model: 0.9520958083832335 Test Precision of the Model: 0.9473684210526315 Training Recall of the Model: 0.9520958083832335 Test Recall of the Model: 0.8 Training F1-Score of the Model: 0.9520958083832335 Test F1-Score of the Model: 0.8674698795180723
15. Plotting the Decision Boundary given by the Trained Logistic Regression both on the Training and Test sets
# plotting the decision boundary in the scatter plot of Training and Test Set with labels indicated by colors x_min, x_max = X_train_pca[:, 0].min() - 1, X_train_pca[:, 0].max() + 1 y_min, y_max = X_train_pca[:, 1].min() - 1, X_train_pca[:, 1].max() + 1 xx_train, yy_train = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1)) Z_train = model.predict(np.c_[xx_train.ravel(), yy_train.ravel()]) Z_train = Z_train.reshape(xx_train.shape) x_min, x_max = X_test_pca[:, 0].min() - 1, X_test_pca[:, 0].max() + 1 y_min, y_max = X_test_pca[:, 1].min() - 1, X_test_pca[:, 1].max() + 1 xx_test, yy_test = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1)) Z_test = model.predict(np.c_[xx_test.ravel(), yy_test.ravel()]) Z_test = Z_test.reshape(xx_test.shape) plt.figure(figsize = (20, 6)) plt.subplot(1, 2, 1) plt.contourf(xx_train, yy_train, Z_train) plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c = y_train, s = 30, edgecolor = 'k') plt.xlabel('Training 1st Principal Component') plt.ylabel('Training 2nd Principal Component') plt.title('Scatter Plot with Decision Boundary for the Training Set') plt.subplot(1, 2, 2) plt.contourf(xx_test, yy_test, Z_test) plt.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c = y_test, s = 30, edgecolor = 'k') plt.xlabel('Test 1st Principal Component') plt.ylabel('Test 2nd Principal Component') plt.title('Scatter Plot with Decision Boundary for the Test Set') plt.show()
Corresponding Output
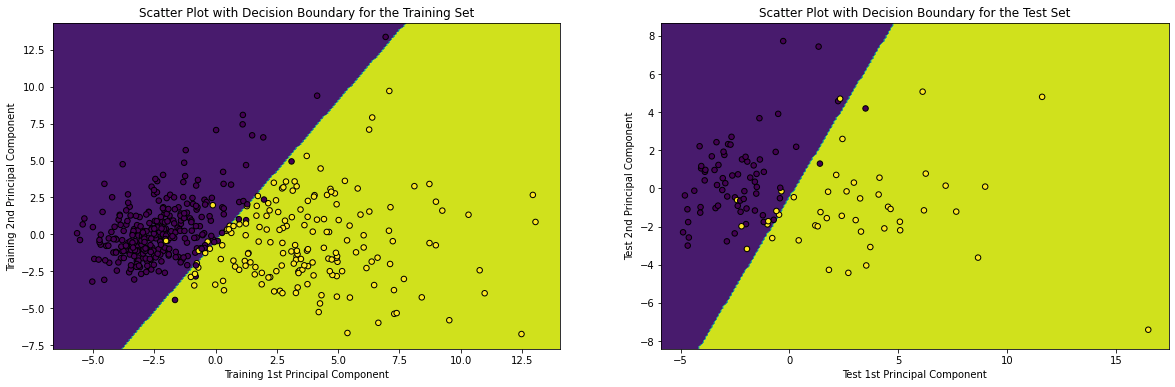
Conclusion
So, from the Decision Boundaries generated above, it can be re-interpreted and re-established that Logistic Regression Classifier belongs to the class of linear models. Apart from that, it can also be concluded that in addition to Performance Metrics like Accuracy, Precision, Recall and F1-Score, Decision Boundary is a visual representation of the Model Performance as well.





.png)


