Any number can be written in the form of binary representations, with just 0 and 1 bits. For example, the binary representation of 2 is 10, 7 is 111, and 8 is 1000. So in this article, we will discuss the Sort Integers By The Number Of 1 Bits leetcode problem based on Dynamic Programming.
Sort Integers by the Number Of 1 Bits problem
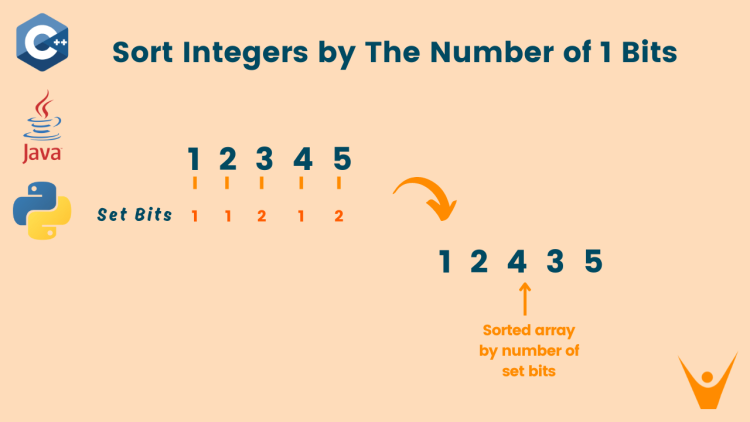
In the Sort Integers by the Number of 1 Bits problem, we have given an integer array and we have to sort this array according to the number of set bits of each integer. If there is a tie, you should sort them in ascending order.
Let’s understand this with an example:
Input: [1, 2, 3, 4, 5]
Output: [1, 2, 4, 3, 5]
Explanation: Integers having set bit 1: 1, 2, 4 as shown in the image
Integers having set-bit 2: 3, 5 as shown in the image
Bubble Sorting Approach
Using Bubble sorting to sort integers by the number of 1 bits, we will calculate the total number of set bits (bits with value 1) for each integer in the array and store them in another array with their indexes. Once we have calculated all the set-bits, we will sort the array using bubble sort in which we will keep on pushing the large value at the end of the array.
Here’s how that will happen. Take this example:
- First, create a vector of pairs that will store the number of set bits and the index of that set bits.
- Now calculate set bits for all the integers in the array and store them in the vector.
- Now sort them by pushing the largest value at the end of the array. As you can see in this example.
- Now create another vector and store the values of the integers from the original array associated with the indexes in the sorted array.
The time complexity for the above solution is O(n^2) where n is the size of the array. As we are doing bubble sort whose time complexity is O(n^2). So the overall time complexity is O(n^2). The space complexity for the above code is O(n) as we are storing the value in another vector for sorting.
Optimized Approach: Sorting Function
In the previous approach, we are doing bubble sort which causes our time complexity to O(n^2) which is huge. To reduce this time complexity we can use a hash map which reduces the time complexity to O(n log(n)).
But we can also reduce the time complexity by using an in-built function i.e. sorting. If you do not want to solve it using the inbuilt function, you can also solve it using merge sort.
Let’s examine this approach step by step:
- First, create a vector of pairs that will store the number of set bits and the index of that set bits.
- Now calculate set bits for all the integers in the array. This could be done by iterating over the number till it becomes 0 and performing an AND operation with that number and 1.
- If it returns 1 after the operation means the bit present at the 0th position is set. Now increase your count by 1. Now right-shift the number and repeat the whole process till we reach 0.
- Now sort them by using the inbuilt sort function
- Now create another vector and store the values of the integers from the original array associated with the indexes in the sorted array.
The time complexity is now O(n log(n)) where n is the size of the array. As we are doing merge sort whose time complexity is O(n log(n)). So the overall time complexity is O(n log(n)). The space complexity is O(n) as we are storing the value in another vector for sorting.
Sorting Original Array
In the above approaches, we are sorting our resultant array. We can also solve this question by sorting the given array. If the original array is sorted means all the values are already in ascending order so we will create a vector of vector. Each index represents a total number of set bits and stores the integers having that set bit.
Here’s how to do it:
- First sort the given array by either inbuilt function or merge sort.
- After that create vector of vector of size 32. At most 31 set bits are possible.
- Now traverse each integer in the array and calculate the total number of setbits present in each integer. Store that integer in the vector corresponding to the total number of set bits.
- Now traverse each vector and traverse integers stored in it. Stores them in a new array in the same order they are stored in the vector.
Now we have the process in hand, we just have to code it.
C++ Code
Here is the C++ program to Sort Integers By The Number of 1 Bits:
#include<bits/stdc++.h>
using namespace std;
int binary_search(vector<int>& v,int target, int p){
int r=v.size();
int start=0,end=r-1,ans=-1;
while(start<=end){
int mid=start+((end-start)/2);
if(target > v[mid]){
start=mid+1;
}
else if(target < v[mid]){
end=mid-1;
}
else {
ans=mid;
if(p)start=mid+1;
else end=mid-1;
}
}
return ans;
}
int main(){
vector<int>arr = {2, 3, 4, 4, 4, 5, 5, 6};
int target = 4;
int first = binary_search(arr, target, 0);
int last = binary_search(arr, target, 1);
cout<<"First position of "<<target<<" is: "<<first<<endl;
cout<<"Last position of "<<target<<" is: "<<last<<endl;
return 0;
}
Java Code
Here is the solution in Java:
import java.util.*;
class SortFunction {
public static List<Integer> sortFun(List<Integer> arr) {
Collections.sort(arr);
List<List<Integer>> v = new ArrayList<>(32);
for (int i = 0; i < 32; i++) {
v.add(new ArrayList<>());
}
for (int i = 0; i < arr.size(); i++) {
int x = 0;
int y = arr.get(i);
while (y > 0) {
if ((y & 1) == 1) x++;
y >>= 1;
}
v.get(x).add(arr.get(i));
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < 32; i++) {
for (int j = 0; j < v.get(i).size(); j++) {
ans.add(v.get(i).get(j));
}
}
return ans;
}
public static void main(String[] args) {
List<Integer> arr = Arrays.asList(1, 2, 3, 4, 5);
List<Integer> res = sortFun(arr);
// output is 1 2 4 3 5
for (int i = 0; i < res.size(); i++) {
System.out.print(res.get(i) + " ");
}
}
}Python Code
We can program it with Python also:
def sort_fun(arr): arr.sort() v = [[] for _ in range(32)] for num in arr: x = 0 y = num while y: if y & 1: x += 1 y >>= 1 v[x].append(num) ans = [] for i in range(32): ans.extend(v[i]) return ans if __name__ == "__main__": arr = [1, 2, 3, 4, 5] res = sort_fun(arr) # output is 1 2 4 3 5 for num in res: print(num, end=" ")
Output:
1, 2, 4, 3, 5The time complexity to Sort Integers by the Number of 1 Bits problem will be O(N log(N)) as we are storing the array using merge sort whose time complexity is O(N log(N)). The space complexity is O(N).
Here you might be confused that it should be O(32) are the size of the vector is 32 but you are creating a vector of vector and inside this, we are storing all the integers present in the array. So the space complexity is O(N).
Notice how the optimized approach is better when compared with others:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n^2) | O(n) | We are using bubble sort whose time complexity is O(n^2). |
| Optimized | O(n log(n) ) | O(n) | We are using merge sort or an inbuilt function whose time complexity is O(n log(n)). |
| Sorting Original Array | O(n log(n) ) | O(n) | Here instead of sorting the resultant array, we are sorting our actual array. |
Conclusion
This is a complete solution to Sort Integers by the Number of 1 Bits leetcode problem. We had seen overall 3 approaches in which we found out the best way of sorting is merge sort. Finding a total number of set bits helps you with many questions related to Dynamic Programming.