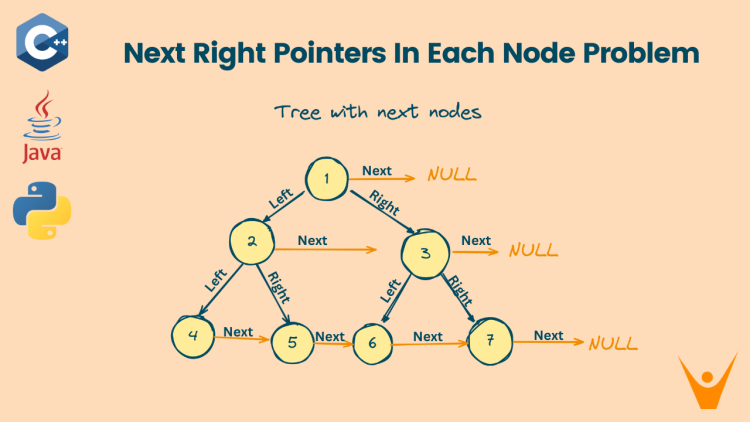
A perfect binary tree is where all leaves are on the same level with every parent having two children. In this article, we will discuss the leetcode problem where we will Populate Next Right Pointers In Each Node based on a perfectly balanced binary tree.
Next Right Pointers In Each Node Problem
In this problem, we are given a perfectly balanced binary tree where all the leaf nodes of the tree are at the same level. We have to place the right pointers as the next node in each node. If there is no right node present mark its next node as NULL.
Let’s examine this with an example:
In the above example, orange lines indicate the next pointer to each node.
The basic approach to solving this question is to visit each node find its level and store that node in a map according to its level. After traversing the whole array we will traverse the map according to levels and keep marking the next node with the next value of that level. If it is the last node we will mark its next node NULL.
Let’s examine the approach step by step:
- First, create a hash map that will store the nodes of the tree level-wise.
- After that create a function that will take the current node and level as variables, now push the value of a node in the hash map according to its level.
- After that call the function for the left and the right node by increasing the level by 1.
- Once we have visited the whole tree, call the hash map and mark the next node with the next value of that level. If the next value is not present mark its next node NULL.
The time complexity for the above process is O(n) as we are visiting the tree once using DFS. DFS time complexity is O(n) so the overall time complexity is O(n). The space complexity will be O(n) as we are storing the values into the hash map whose time complexity is O(n).
Optimized Solution
In the above approach, we are storing the values into the hash map which is taking O(n) space complexity. To reduce this space complexity to constant space we will do level-wise traversal. Here’s how to do it:
- First, create a queue that will store the nodes on a level.
- Store the root node in the queue. After pushing the root node push NULL. NULL indicates that this level ends here. After that next level will start.
- Now iterate the queue till its size becomes 0.
- Now take out the current node from the queue and store it in a temp variable. Check if the next node present in the queue is NULL or not.
- If it is not NULL mark the next of temp as this node If it is NULL mark the next of temp NULL and take out that node from the queue. Push the NULL node in the queue.
- After that push the left and the right node in the queue.
Now, it’s time to implement it.
C++ Code
Below is the C++ implementation to populate the next right pointers in each node:
#include<bits/stdc++.h>
using namespace std;
class Node{
public:
int val;
Node* left;
Node* right;
Node* next;
Node(int x){
val = x;
left = NULL;
right = NULL;
next = NULL;
}
};
Node* find_next(Node* root){
if(root == NULL) return root;
queue<Node*>q;
q.push(root);
q.push(NULL);
while(q.size()){
Node* temp = q.front();
if(temp ==NULL){
q.pop();
if(q.size()) q.push(NULL);
continue;
}
q.pop();
if(q.front()){
temp->next = q.front();
}
if(temp->left) q.push(temp->left);
if(temp->right) q.push(temp->right);
}
return root;
}
int main(){
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
find_next(root);
return 0;
}Java Code
Below is the Java program for the solution:
import java.util.LinkedList;
import java.util.Queue;
class Node {
int val;
Node left, right, next;
Node(int x) {
val = x;
left = null;
right = null;
next = null;
}
}
class NextPointer {
static Node findNext(Node root) {
if (root == null) return root;
Queue<Node> q = new LinkedList<>();
q.add(root);
q.add(null);
while (!q.isEmpty()) {
Node temp = q.poll();
if (temp == null) {
if (!q.isEmpty()) q.add(null);
continue;
}
if (q.peek() != null) {
temp.next = q.peek();
}
if (temp.left != null) q.add(temp.left);
if (temp.right != null) q.add(temp.right);
}
return root;
}
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
findNext(root);
}
}Python Code
We can implement it in Python also:
from queue import Queue class Node: def __init__(self, x): self.val = x self.left = None self.right = None self.next = None def find_next(root): if root is None: return root q = Queue() q.put(root) q.put(None) while not q.empty(): temp = q.get() if temp is None: if not q.empty(): q.put(None) continue if not q.empty() and q.queue[0] is not None: temp.next = q.queue[0] if temp.left: q.put(temp.left) if temp.right: q.put(temp.right) return root if __name__ == "__main__": root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.left = Node(6) root.right.right = Node(7) find_next(root)
The time complexity to populate the next right pointers in each node is O(n). The space complexity is O(1) as we are not using any extra space. Here’s how both the approaches compare and reduce space complexity:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n) | O(n) | We are storing the values into the hash map whose space complexity is O(n). |
| Optimized | O(n) | O(1) | We are doing level-wise traversal which reduced our space complexity to O(1). |
Conclusion
In this article, we discussed various methods to populate Next Right Pointers In Each Node problem from leetcode. We had seen that by using hash-map we are taking extra O(n) space which can be reduced if we use level-wise traversal. Now, check how to print the right-side view of a binary tree, which is also as interesting.