One of the fun leetcode problems is related to Permutation in String. You can solve it using various methods like backtracking, and recursion, which we will learn how to do right here.
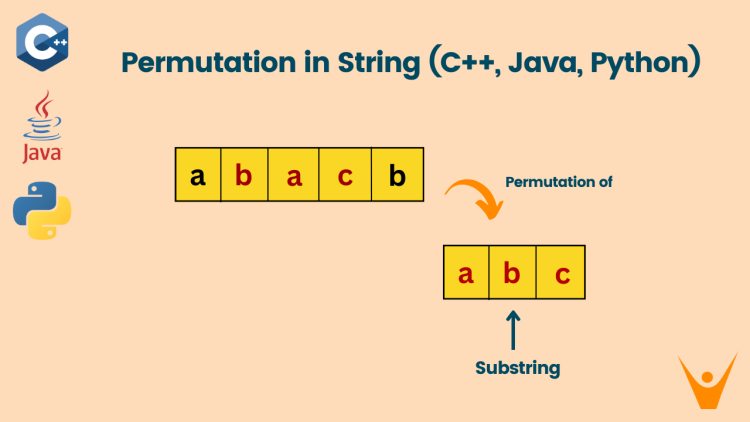
Permutation in String problem
A permutation is a set of all the possible values which is formed by rearranging the given value. For example, permutations of 123 are 123, 132, 213, 231, 312, and 321. In all the permutations, the frequency of each element should remain the same as in the given value.
In the Permutation in String problem, you have given two strings. String ‘A’ and string ‘B’. You have to find whether any permutation of string A lies in string B. If it is returned true, if not, return false.
Here is an example:
Input: A: ab
B: cdbaha
Output: True
Explanation: Permutations of ab are ab and ba. In “cdbaha” ba lies inside it. This means the permutation of a is a substring of string B.
The naive solution is to find out all the permutations of string A and then check if any of the strings is a substring of B. If it is returned true. If not return false.
Let’s examine this approach step by step:
- First, find all the permutations of the string. You can find this by backtracking.
- After finding all the permutations go to each permutation and check if it lies inside string B or not. You can find this by sliding the window approach. In this approach, you have to take a substring starting from 0 and of size the same as A and then keep on adding the next index value and removing the previous index values.
- If you find any substring in B same as the permutation of string A return true.
- If not, return false.
The time complexity of the above solution is O((n*n!) + (k*n!)) where n is the size of string A and k is the size of string B. As we are calculating the permutation of string A whose time complexity is O(n*n!) and for finding whether the permutation lies in string B or not it took O(k*n!) time complexity so overall time complexity is O((n*n!) + (k*n!)).
The space complexity is O(n!) as there are total n!. A permutation is possible for string A.
Optimized Approach
In the above approach, we find all permutations of a string, which leads to a significant increase in time complexity. Instead of finding the permutations of the string, we can utilize the properties of permutations.
In a permutation, the frequency of each element remains the same across all permutations. Therefore, we store the frequency of each element in an array and check in string B whether any substring has the same frequency or not. If the frequencies match, we return true; otherwise, we return false.
Let’s learn how to do it:
- First, check if the size of A is greater than B and return false.
- First, create an array arr, of size 26 which stores the frequency of each character in string A.
- Store the frequency of each element in string A.
- Create another array of size 26 and name this array a temp array. Now run a loop of size n (n is the size of string A) and store the frequency of each character in string B till size n.
- Check if the temp array is the same as arr. If it is returned true.
- If not check for the next n elements in string B by sliding window approach and check at any point temp become equal to array arr return true.
- At last return false.
Now is the time to code it.
C++ Code
Here is the C++ solution for Permutation in String problem:
#include<bits/stdc++.h>
using namespace std;
bool check_permutation(string A, string B){
vector<int>v(26,0);
vector<int>temp(26,0);
// if s1 length is greater than s2
int k=A.size();
if(k>B.size()) return false;
for(int i=0;i<k;i++) {
v[A[i]-'a']++;
}
for(int i=0;i<k;i++){
temp[B[i]-'a']++;
}
if(temp==v) return true;
int ind=1;
for(int i=ind;i+k<=B.size();i++){
temp[B[i-1]-'a']--;
temp[B[i+k-1]-'a']++;
if(temp==v) return true;
}
return false;
}
int main(){
string A = "otut";
string B = "favtutor";
bool ans = check_permutation(A, B);
ans? cout<<"True"<<endl: cout<<"False"<<endl;
return 0;
}Java Code
We can implement the approach in Java as well:
import java.util.Arrays;
public class Main {
static boolean checkPermutation(String A, String B) {
int[] v = new int[26];
int[] temp = new int[26];
// if s1 length is greater than s2
int k = A.length();
if (k > B.length()) return false;
for (int i = 0; i < k; i++) {
v[A.charAt(i) - 'a']++;
}
for (int i = 0; i < k; i++) {
temp[B.charAt(i) - 'a']++;
}
if (Arrays.equals(temp, v)) return true;
for (int i = 1; i + k <= B.length(); i++) {
temp[B.charAt(i - 1) - 'a']--;
temp[B.charAt(i + k - 1) - 'a']++;
if (Arrays.equals(temp, v)) return true;
}
return false;
}
public static void main(String[] args) {
String A = "otut";
String B = "favtutor";
boolean ans = checkPermutation(A, B);
System.out.println(ans ? "True" : "False");
}
}Python Code
Here is the Python program for Permutation in String problem:
def check_permutation(A, B):
v = [0] * 26
temp = [0] * 26
# if s1 length is greater than s2
k = len(A)
if k > len(B):
return False
for i in range(k):
v[ord(A[i]) - ord('a')] += 1
for i in range(k):
temp[ord(B[i]) - ord('a')] += 1
if temp == v:
return True
ind = 1
for i in range(ind, len(B) - k + 1):
temp[ord(B[i - 1]) - ord('a')] -= 1
temp[ord(B[i + k - 1]) - ord('a')] += 1
if temp == v:
return True
return False
if __name__ == "__main__":
A = "otut"
B = "favtutor"
ans = check_permutation(A, B)
print("True" if ans else "False")Output:
TrueThe time complexity to solve the Permutation in a String is O(n + k), where n is the size of string A and k is the size of string B. This is because we are running a loop to store the frequency of all elements in the string A whose time complexity is O(n). After that, we check every substring of size n has the same frequency as of array arr, which takes O(k) time complexity.
The space complexity is O(26) ~ O(1), As we are just storing the frequency of each character.
Here is the comparison that shows how the optimized approach is better:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O((n* n!) +(k*n!)) | O(n!) | We are finding all the permutations which laid our time complexity to O(n*n!) |
| Optimized Approach | O(n + k) n: the size of A k: the size of B | O(n!) | We are using the array to store the frequency of each element in string A. |
Conclusion
We have seen various approaches to solve the Permutation in String problem from leetcode. The storing frequency approach saved our time complexity to a large extent. You can now solve other questions based on the Sliding window approach, Valid Anagram, etc.