Partition Equal Subset Sum (C++, Java, Python)

The array contains many programming problems asked in interviews, and one of the interesting ones involves balancing the sum of numbers into two equal subsets. In this article, we will discuss the Partition Equal Subset problem from leetcode and try to solve it using recursion, and optimize it using dynamic programming.

Partition Equal Subset Sum Problem

In this Partition Equal Subset Sum problem, we are given an array with N positive integers. We need to check if we can divide the array into two subsets so that the sum of elements of each subset is equal. If this is possible we have to return true otherwise false.

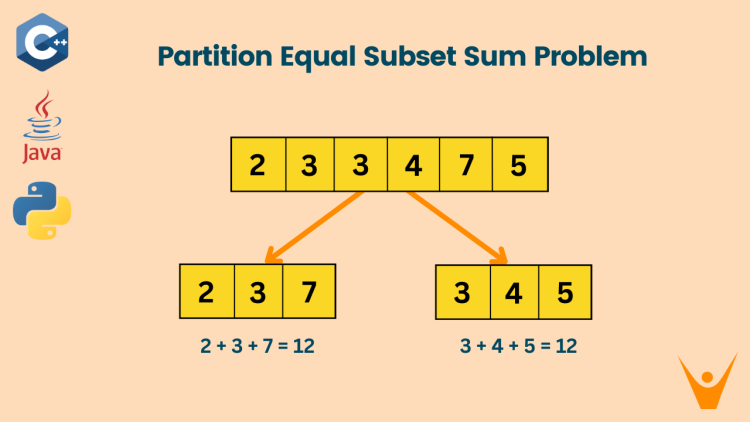
Let us take an example:

Input: [2,3,3,4,7,5]

Output: [2,3,7] [3,4,5]

So two main steps to solve the problem: we will calculate the sum of all the elements. If the sum is odd then partition will never be possible. But, if sum is even then we will find if there is a subset with sum = sum/2 then it is possible to find subsets.

Brute Force using Recursion

Recursion helps us to solve a problem in which we have to explore all cases and in this problem, we have to explore all possible cases to return our answer. In this approach, we have to find a subset whose sum is equal to sum/2.

Here are the steps to be followed in this approach:

We will start from the last index with a target value of sum/2 for each index we have 2 choices either to pick that element or to not pick that element
So if we pick that element our target is equal to target – arr[ind] and we just move to another index.
For not picking there will be no change in target value we just move to another index
We will check base cases at every recursive call.

Base cases:

If the target value becomes 0 at some point means we have found a subset then we will return a true
If we reach the final index and arr[index] is equal to the target then we will return true.

Complexity Analysis

The time complexity of solving the Partition Equal Subset Sum problem using recursion is O(2^N) because, for each index, there are two recursive calls: one when we include the element in the subset and another when we exclude it. The space complexity includes the space used by recursive stack space in worst case the maximum depth of the call stack is equal to the size of the array, i.e. O(n).

Dynamic Programming Approach

The recursive approach will solve the problem but it is not an effective way to solve the problem so to optimize our solution we will memoize our solution. Below are the steps to memoize our solution:

Firstly we will create a 2-D array of dimensions (N+1)*(sum+1)
Now when the recursive function with the input array, size, the target sum, and the dp array as parameter invokes.
Then If the target sum is zero, return true, or if the size is zero and the target sum is not zero, return false
If the solution for this subproblem has been previously computed, return the stored answer from the dp array.
Otherwise, we will compute the solution for this subproblem using the recursive formula from the earlier approach and store the result in the dp array.
At last, we will return the answer.

C++ Code

Below is the C++ program to solve the Partition Equal Subset Sum problem:

#include <iostream>
#include <vector>

using namespace std;

bool canPartitionHelper(vector<int>& nums, int n, int sum, vector<vector<int>>& dp) {
    // Base cases
    if (sum == 0) {
        return true;
    }
    if (n == 0 && sum != 0) {
        return false;
    }

    // If the result for this subproblem is already calculated, return it
    if (dp[n][sum] != -1) {
        return dp[n][sum];
    }

    // Recursive cases
    // Check if including or excluding the current element leads to a valid partition
    if (nums[n - 1] <= sum) {
        dp[n][sum] = (canPartitionHelper(nums, n - 1, sum - nums[n - 1], dp) || 
                      canPartitionHelper(nums, n - 1, sum, dp));
    } else {
        dp[n][sum] = canPartitionHelper(nums, n - 1, sum, dp);
    }

    // Return the result for this subproblem
    return dp[n][sum];
}

bool canPartition(vector<int>& nums) {
    int totalSum = 0;
    for (int num : nums) {
        totalSum += num;
    }

    // If the total sum is odd, partition is not possible
    if (totalSum % 2 != 0) {
        return false;
    }

    int target = totalSum / 2;
    int n = nums.size();

    // Create a 2-D vector for memoization and initialize with -1
    vector<vector<int>> dp(n + 1, vector<int>(target + 1, -1));

    // Call the recursive helper function
    return canPartitionHelper(nums, n, target, dp);
}

int main() {
    vector<int> nums = {2, 3, 3, 4, 7, 5};
    bool result = canPartition(nums);

    cout << (result ? "True" : "False") << endl;  // Output: True

    return 0;
}

Java Code

You can implement it in Java as well:

import java.util.Arrays;

public class PartitionEqualSubsetSum {
    public static boolean canPartition(int[] nums) {
        int totalSum = Arrays.stream(nums).sum();

        // If the total sum is odd, partition is not possible
        if (totalSum % 2 != 0) {
            return false;
        }

        int target = totalSum / 2;
        int n = nums.length;

        // Create a 2D array for memoization and initialize with -1
        int[][] dp = new int[n + 1][target + 1];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }

        // Call the recursive helper function
        return canPartitionHelper(nums, n, target, dp);
    }

    private static boolean canPartitionHelper(int[] nums, int n, int sum, int[][] dp) {
        // Base cases
        if (sum == 0) {
            return true;
        }
        if (n == 0 && sum != 0) {
            return false;
        }

        // If the result for this subproblem is already calculated, return it
        if (dp[n][sum] != -1) {
            return dp[n][sum] == 1;
        }

        // Recursive cases
        // Check if including or excluding the current element leads to a valid partition
        if (nums[n - 1] <= sum) {
            dp[n][sum] = (canPartitionHelper(nums, n - 1, sum - nums[n - 1], dp) ||
                          canPartitionHelper(nums, n - 1, sum, dp)) ? 1 : 0;
        } else {
            dp[n][sum] = canPartitionHelper(nums, n - 1, sum, dp) ? 1 : 0;
        }

        // Return the result for this subproblem
        return dp[n][sum] == 1;
    }

    public static void main(String[] args) {
        int[] nums = {2, 3, 3, 4, 7, 5};
        boolean result = canPartition(nums);

        System.out.println(result);
    }
}

Python Code

Here is the Python code the dynamic programming approach:

def can_partition(nums):
    total_sum = sum(nums)

    # If the total sum is odd, partition is not possible
    if total_sum % 2 != 0:
        return False

    target = total_sum // 2
    n = len(nums)

    # Create a 2D array for memoization and initialize with -1
    dp = [[-1 for _ in range(target + 1)] for _ in range(n + 1)]

    # Call the recursive helper function
    return can_partition_helper(nums, n, target, dp)


def can_partition_helper(nums, n, sum, dp):
    # Base cases
    if sum == 0:
        return True
    if n == 0 and sum != 0:
        return False

    # If the result for this subproblem is already calculated, return it
    if dp[n][sum] != -1:
        return dp[n][sum] == 1

    # Recursive cases
    # Check if including or excluding the current element leads to a valid partition
    if nums[n - 1] <= sum:
        dp[n][sum] = 1 if (can_partition_helper(nums, n - 1, sum - nums[n - 1], dp) or
                           can_partition_helper(nums, n - 1, sum, dp)) else 0
    else:
        dp[n][sum] = 1 if can_partition_helper(nums, n - 1, sum, dp) else 0

    # Return the result for this subproblem
    return dp[n][sum] == 1


# Example usage
nums = [2, 3, 3, 4, 7, 5]
result = can_partition(nums)
print(result)

Output:

True

Complexity Analysis

The Time complexity is O(N * sum), where N is the number of elements in the array and sum is the sum of all elements. The Space complexity is O(N * sum) due to the memoization table.

Memoization is also useful when solving the subset sum problem.

Conclusion

In conclusion, we solved the Partition Equal Subset Sum problem from leetcode with a recursive approach and dynamic programming approach. We have also discussed the implementation in C++, Java, and Python.