The Binary Search is the best way to find a value in any sorted array. Similarly, we can also search for a given value in the sorted matrix. This article will discuss the leetcode problem “Kth Smallest Element in a Sorted Matrix” using Binary Search.
Kth Smallest Element in a Sorted Matrix problem
In the Kth Smallest Element in a Sorted Matrix problem, we are given a matrix of size (n*m). The rows and columns of this matrix are sorted in ascending order. We have to find the Kth smallest element in this matrix.
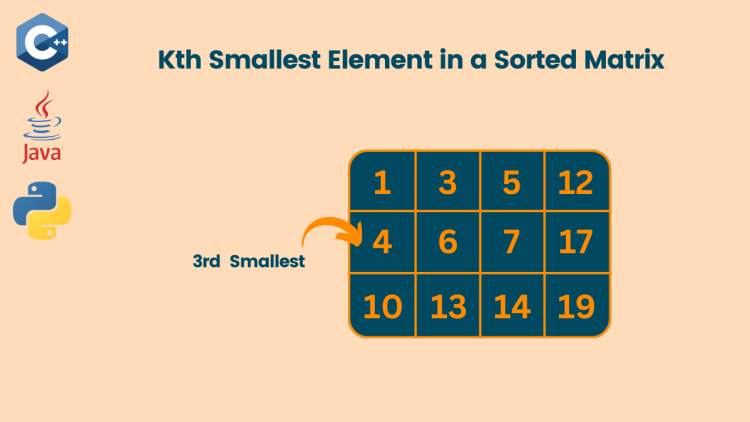
Not that the rows and columns are sorted, not the whole matrix, as shown here, with the first row having 1, 3, 5, and 12, but the second row’s first element being 4, which is greater than 1 but less than 5.
Now the 9th smallest element in the given matrix is 13, as we can see by arranging these elements into the sorted array.
Naive Brute Force Approach
To find the Kth element in the sorted matrix, one naive approach that comes to mind is to store all the elements of the matrix in an array or vector. After that sort that array. The Kth element of the sorted array will be the answer.
Let’s look at this approach step by step:
- The first step is to create an empty array of size (n*m). Here n is the number of rows in the matrix and m is the number of columns in the matrix.
- The second step is to store all the matrix values in the array.
- The third step is to sort that array.
- The final step is to print the kth element from the array.
The time complexity of the above code is NLog(N). Here N=(n*m). As N for two loops which is sorting value into the array and Nlog(N) for sorting array, the time complexity will be N+ Nlog(N) ~ Nlog(N). The space complexity of the above code is O(N) as we need an (n*m) size array to store all the values in the matrix.
Max Heap Approach
As the above approach is taking up too much extra space, this can be reduced by using the min or max heap.
In the minimum or maximum heap, the values are already sorted in stored order, so we will maintain a max heap of size k; in that case, the Kth smallest element would be the first element of the max heap. This will reduce our space complexity to O(k).
Here is how to do it:
- The first step is to create a max heap or a priority queue.
- Now store elements in it. Check that at each time the size of the max heap is less than or equal to k. If the size exceeds at any point in time, remove the element from the top of the priority queue.
- Return the top element from the priority queue.
The time complexity will remain the same i.e. Nlog(N) where N= (n*m). Inserting the values into the priority queue will take Log(N) time, and as we are running two loops one of size n and the other of size m it becomes Nlog(N).
The space complexity will reduce to O(k) from O(N) as at each point size of the priority queue is less than or equal to k.
Optimized Binary Search Approach
The above approach reduces the space complexity, but it still has a large time complexity, which can be reduced with the help of a binary search as the matrix is already sorted. Here comes the binary search!
Binary search can be used here by finding the middle element and then finding the position of that element in the matrix.
Look at this matrix:
- In the matrix if we need to find the 3rd smallest value. We will start with the middle of 1st and 4th i.e. 2.
- The position of 2 is 2. So we will look at the right side by updating our low value to mid+1. So the new value will be the middle value of 3 and 4 i.e. 3.
- The position of 3 is 3. So we will look at the right side by updating our high to mid. As the low and high are both equal to 3 our loop will break.
- It will print the low value.
Now we have to do the below process:
- First make two variables: one is storing the minimum value, and the other is storing the maximum value, say, low for the minimum and high for the maximum. Calculate the middle value from those lows and highs, say mid.
- Count the number of values that are lower and equal to the mid-value using the upper bound, which results in all the values that are less than or equal to the middle value.
- If the count is greater than or equal to k, then update the high to mid as the value will lie on the left side. Otherwise, update low to mid+1.
- Now repeat the same process till the low is less than the high and at last return the low value.
Another similar problem is to Find Peak Element in an Array using Binary Search.
C++ Code
Here is the C++ program to find the kth smallest element in a sorted matrix:
#include <bits/stdc++.h>
using namespace std;
int kthSmallest(vector<vector<int>>& arr, int k) {
int n= arr.size();
int m=arr[0].size();
int low=arr[0][0], high=arr[n-1][m-1]; // initializing the low and high value
while(low<high){
int mid= (low+high)/2; // calculating middle-value
int count=0; // count variable to track the total value less than equal to the middle
for(int i=0; i<n; i++){
count+= upper_bound(arr[i].begin( ), arr[i].end(), mid)-arr[i].begin();
}
if(count<k){
low=mid+1; // updating low value as count is less than k => value lies in right side
}else{
high=mid; // updating high value as count is greater than k => value lies in left side
}
}
return low; // returning the kth smallest value
}
int main(){
// matrix.
vector<vector<int>>v = {{1, 3, 5, 12},
{4, 6, 7, 17},
{10, 13, 14, 19}};
int k = 7;
// calling function kth smallest that return the 7th smallest elemet in the given matrix.
int value = kthSmallest(v,k);
// print the value.
cout<<value<<endl;
return 0;
}Java Code
Here is the binary search solution in Java:
import java.util.*;
class KthSmallestElement {
public static int binarySearch(int []arr, int k){
int n = arr.length;
int low = 0, high = n-1;
while(low <= high){
int mid = (low + high)/2;
if( arr[mid] <= k ) {
low = mid+1;
}else {
high = mid-1;
}
}
return low;
}
public static int kthSmallest(int[][] arr, int k) {
int n = arr.length;
int m = arr[0].length;
int low = arr[0][0], high = arr[n - 1][m - 1];
while (low < high) {
int mid = (low + high) / 2;
int count = 0;
for (int i = 0; i < n; i++) {
int x = binarySearch(arr[i], mid);
count = count + x;
}
if (count < k) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
}
public static void main(String[] args) {
int[][] v = { { 1, 3, 5, 12 }, { 4, 6, 7, 17 }, { 10, 13, 14, 19 } };
int k = 7;
int value = kthSmallest(v, k);
System.out.println(value);
}
}Python Code
Below is the Python program for this:
def kth_smallest(arr, k):
n = len(arr)
m = len(arr[0])
low = arr[0][0]
high = arr[n - 1][m - 1]
while low < high:
mid = (low + high) // 2
count = 0
for i in range(n):
count += len([x for x in arr[i] if x <= mid])
if count < k:
low = mid + 1
else:
high = mid
return low
if __name__ == "__main__":
v = [[1, 3, 5, 12],
[4, 6, 7, 17],
[10, 13, 14, 19]]
k = 7
value = kth_smallest(v, k)
print(value)Output:
10The time complexity of the above code is reduced to O(x * n * log(n)), where x = log(high-low). x for binary search, n for iterating over the loop, and log(n) for the upper bound. Space complexity will be O(1).
Here is how the three approaches are compared:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force Approach | O(N log(N)) N = (n*m) | O(N) | We are storing all the matrix values in the array and then sorting those values. |
| Max Heap Approach | O(N log(N)) | O(k) k is the same as the index given. | We are using max heap to store the k smallest element at every index. |
| Optimized Approach | O(x*n*log(n)) x = log(high – low) | O(1) | We are using the binary search here whose time complexity is Log(n). |
Conclusion
In this article, we learn how we can reduce our time complexity to find the kth smallest element in a sorted matrix from n to log(n) with the help of binary search. This a very interesting leetcode problem to solve.