There are many situations in our daily life where we need to choose the path best for us to reach our destination. In programming, one such problem in Data Structures and Algorithms is the Minimum Path Sum, which we will try to solve using various approaches.
Minimum Path Sum Problem
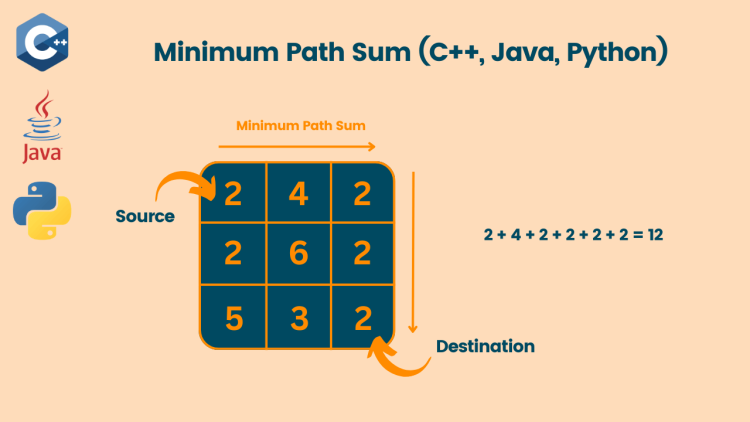
In the Minimum Path Sum problem, we are given a 2D grid of size m x n, and we have to find the path from the top-left element to the right element, with the sum of those elements being the minimum.
Let’s understand this with an example:
Input:
matrix = [ [2,4,2],
[2,6,2],
[5,3,2] ]Output:
12
The path 2 → 4 → 2 → 2 → 2, which sums up to 12 has the minimum sum.
Recursion Approach
The simplest approach that will first come to our mind is to find out all the possible paths and compare them to find the lowest sum path, that would be our answer. Since we need to perform the repetitive steps, we can make use of recursion to try out all possible paths. Here is how we can do it:
- Call a recursive function by passing i and j as 0, where i and j represent the row and column index respectively.
- The base case for the recursive function is when i>=m or j>=n, we need to stop calling the function.
- If we are at the right-bottom element, we can return the value of that element, as we have reached our destination.
- Otherwise, if we are at any other element, we have two options, i.e. to go right or down:
- Add the element to sum1 and call the function by passing i as i+1, as we have moved right, i.e. sum1 = matrix[i][j] + solve(i+1, j)
- To move down, perform the same in sum2 but pass j+1 instead of j, i.e. sum2 = matrix[i][j] + solve(i, j+1)
- Return the minimum of sum1 and sum2.
The time complexity for this solution will be O(2^(m*n)), where m and n are the number of rows and columns of the matrix. The space complexity is O(m*n ) which is used by the call stack.
Memoization Approach
We can improve the time complexity of the recursive solution by using the concept of memoization. Since we are calculating the sum of all the paths, we can store them to reuse them for overlapping paths. We can use the concept of dynamic programming in the following way:
- Create the same recursive function as done in the recursive approach, we will apply the concept of dynamic programming in this approach.
- Create a 2D dp array of size m x n.
- Before calculating again the sum for the path, we will first check it in our dp array ( dp[i][j] ), if we have calculated it before, we can simply use it.
- Else, calculate the sum and set dp[i][j] = sum, so that we can use it again for the sub-problems.
The time complexity for this approach will be O(m*n), where m and n are the number of rows and columns of the matrix. There will be a maximum of m*n calls of recursion. The space complexity is O(m*n) which is used by the 2D dp array and recursion stack.
Tabulation Approach
In the previous approach, we started from i = 0 and j = 0, and moved to the bottom right column, so it was a top-down approach. We can use a bottom-up approach also to solve the same problem. Here is how we can use the Tabulation approach:
- Create a 2D dp array of size m*n.
- Initialize the base conditions as dp[0][0] = matrix[0][0], as if we have only one element left, we have to take it to reach our destination.
- Use two nested loops to fill the dp array starting from the bottom except for i=0 and j=0, as we have already filled the value for them.
- We have two options at each point, i.e. dp[i-1][j] and dp[i][j-1], take the minimum of them and add it to matrix[i][j] to get the minimum sum for this path.
- Return dp[m-1][n-1] as the answer.
The time complexity now will be O(m*n), where m and n are the numbers of rows and columns of the matrix since we are using the nested loops from 0 to m and 0 to n. The space complexity is also O(m*n).
Optimal Approach: Tabulation + Space Optimization
As we have seen in the above approaches, we have significantly reduced the time complexity, but space is still an issue for us. To reduce the space complexity, we need to optimize our tabulation solution.
We can observe that the answer for any sub-problem depends on two things, dp[i-1][j] and dp[i][j-1], which is nothing but a previous value of the same row, and the same value from the previous row.
In simpler language, our answer for each point depends on just the current and previous row. So instead of storing answers for each point, we can store just the current and previous rows. This will eventually bring the complexity down to O(2*n).
The following modifications are needed to be done in the tabulation solution:
- Use two arrays, i.e. current and previous of size n, instead of a 2d dp array.
- The current[j-1] represents our dp[i][j-1] and previous[j] represents our dp[i-1][j].
- Initialize the current vector inside the loop 0 to m, so that we can calculate its values for each index.
- Update the previous = current once the calculations are performed, as the current row becomes previous when we move to the next row.
- Finally, return the answer as previous[n-1] which is nothing but equal to dp[m-1][n-1].
Let’s take our matrix and look at the steps:
Initialize the previous and current vector:
Iteration 1: Index = 0
Iteration 2: Index = 1
Iteration 3: Index = 2
The answer is equal to the previous[m – 1], i.e. 12.
C++ Code
Here is the C++ program to find the Minimum Path Sum problem:
#include <bits/stdc++.h>
using namespace std;
int main() {
// Input matrix
vector<vector<int>> matrix{
{2, 4, 2},
{2, 6, 2},
{5, 3, 2}
};
// Finding number of rows and columns
int m = matrix.size(), n = matrix[0].size();
// Used to store the previous row's minimum path sums
vector<int> previous(m, 0);
for(int i=0; i<m; i++) {
vector<int> current(m,0);
for(int j=0; j<n; j++) {
if(!(i == 0 && j == 0)) {
// previous column of current row
int left = j > 0 ? current[j-1] : INT_MAX;
// same column of previous row
int up = i > 0 ? previous[j] : INT_MAX;
current[j] = matrix[i][j] + min(left,up);
}
else{
// If we have only one element, it will be the answer
current[j] = matrix[0][0];
}
}
previous = current;
}
// prev[m-1] represents the final result
cout << "Minimum sum path is: " << previous[m - 1];
return 0;
}Java Code
Here is the Java program:
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
// Input matrix
int[][] matrix = {
{2, 4, 2},
{2, 6, 2},
{5, 3, 2}
};
// Finding number of rows and columns
int m = matrix.length, n = matrix[0].length;
// Used to store the previous row's minimum path sums
int[] previous = new int[m];
for (int i = 0; i < m; i++) {
int[] current = new int[m];
for (int j = 0; j < n; j++) {
if (!(i == 0 && j == 0)) {
// Previous column of current row
int left = j > 0 ? current[j - 1] : Integer.MAX_VALUE;
// Same column of previous row
int up = i > 0 ? previous[j] : Integer.MAX_VALUE;
current[j] = matrix[i][j] + Math.min(left, up);
} else {
// If we have only one element, it will be the answer
current[j] = matrix[0][0];
}
}
previous = Arrays.copyOf(current, m);
}
// previous[m-1] represents the final result
System.out.println("Minimum sum path is: " + previous[m - 1]);
}
}Python Code
We can implement it with Python also:
import sys
# Input matrix
matrix = [
[2, 4, 2],
[2, 6, 2],
[5, 3, 2]
]
# Finding number of rows and columns
m = len(matrix)
n = len(matrix[0])
# Used to store the previous row's minimum path sums
previous = [0] * m
for i in range(m):
current = [0] * m
for j in range(n):
if not (i == 0 and j == 0):
# Previous column of current row
left = current[j - 1] if j > 0 else sys.maxsize
# Same column of previous row
up = previous[j] if i > 0 else sys.maxsize
current[j] = matrix[i][j] + min(left, up)
else:
# If we have only one element, it will be the answer
current[j] = matrix[0][0]
previous = current
# previous[m-1] represents the final result
print("Minimum sum path is:", previous[m - 1])Output:
Minimum sum path is: 12The time complexity is also O(m*n), where m and n are the number of rows and columns of the matrix since we are using the nested loops from 0 to m and 0 to n. The space complexity is O(n) which is used by the current and previous arrays.
Below is a comparison of all the approaches to solve this problem, and how combining two methods makes it easier to solve:
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force: Find out all the possible paths using recursion and compare them to find the lowest sum path. | O(2^(m*n)) | O(m*n) |
| Memoization: Use dynamic programming to store the answers for overlapping paths. | O(m*n) | O(m*n) |
| Tabulation: A bottom-up approach is used to solve the problem in the same manner. | O(m*n) | O(m*n) |
| Tabulation + Space Optimization: Instead of storing answers for each point, we can store just the current and previous rows as our answer depends on them only. | O(m*n) | O(n) |
Conclusion
Overall, Minimum Path Sum is an interesting leetcode problem that involves recursion and dynamic programming. We were able to reduce the time complexity from exponential to O(m*n).