Recursion is an amazing way to solve many coding problems, but sometimes we repeatedly solve the same thing we have already solved. This can be reduced with the help of dynamic programming. In this article, we will discuss the popular programming problem called the “Word Break” and get it using dynamic programming.
What is the Word Break Problem?
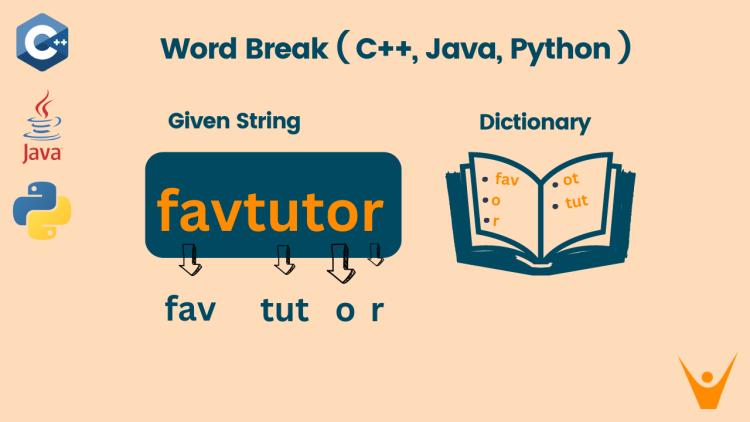
In the Word Break problem, you are given a string and an array containing words that lie in a dictionary. We have to find if we can break the string into substrings such that each substring lies in the dictionary. Note that the same word may be used for more than one substring.
Let’s understand this with an example:
The array given to you is
The simple way to get the answer is by storing the elements of an array in the hash map. After that we will recursively check for the substring if it lies in the hashmap check for the next substring. If all the substring lies in the hash map return true. Otherwise, return false.
Here is how to do it:
- First store elements of the array into the hash map.
- Now create a function that has parameters start index, end index, hash map, and the string.
- Now call the function with a starting index of 0 and an ending index of 0.
- Check if the substring starting from the start index and of length (end-start+1) lies between the hash map or not. If it lies in the hash map check for the next substring.
- If it does not lie between the hashmap call the function by increasing the end to end+1.
- If we reach the last index, return false.
The time complexity for the above approach is O(n*n) where n is the size of the string. As we are recursively calling the function for all the substrings in contains in a given string. The space complexity of the above code is O(n*n) as we are memorizing our previously calculated values into a 2-D array.
But there is a better way possible!
Optimized Approach
In the above approach, we are storing the values of the array in the hash map which increases our memory. Also, we are storing the starting and ending index of the substring which is laid to space complexity of O(n^2).
In the dynamic programming approach to solve the Word Break problem, we will iterate all the words in the array. Check if any of the words can be formed from the substring starting from the start index given to you. If it can be formed check for the index start = start + word. size(). If all the substring contains in the array return true, Otherwise return false.
Let’s examine the step-by-step approach for the above process.
- First, create an array for memorizing the values of the string. Initialize all the values with -1.
- Create a function that will check if we can break the string or not. The function took parameters starting index, string, array, and the memorized array.
- Check if the starting index is equal to the size of the string if it returns 0. As we are out of the string.
- If not, check if we had previously checked for this index or not. If dp[ start ] == -1 means we have not checked it yet. If dp[ start ] == 0 means we cannot break that string. If dp[ start] == 1 means we can break the string.
- If we had not checked this index, iterated over the array and checked if the substring starting from the start till the word length is the same as the word or not. If it is the same check for index start = start + word. size(). If it is not, return false.
Let’s now implement it in programming.
C++ Code
Below is the C++ program for the Word Break problem:
#include<bits/stdc++.h>
using namespace std;
bool word_break(int start, string& s, vector<string>& arr, vector<int>& dp){
if(dp[start]>=0) return dp[start]? true:false;
int n = s.size();
bool flag = false;
for(int i=0;i<arr.size();i++){
int sz = arr[i].size();
if(start + sz > n) continue;
string temp = s.substr(start, sz);
if(temp == arr[i]){
if(start + sz == n) flag = true;
else flag = flag || word_break(start+sz, s, arr, dp);
}
if(flag) break;
}
if(flag) dp[start] = 1;
else dp[start] = 0;
return flag;
}
int main(){
string s = "favtutor";
vector<string>v = {"tut", "fav", "o", "r", "ot"};
// dp array for memorizing.
vector<int>dp(s.size()+2,-1);
(word_break(0, s, v, dp))? cout<<"True"<<endl: cout<<"False"<<endl;
return 0;
}Java Code
You can do it with Java also:
import java.util.*;
public class WordBreak {
static boolean wordBreak(int start, String s, List<String> arr, int[] dp) {
if (dp[start] >= 0) return dp[start] == 1;
int n = s.length();
boolean flag = false;
for (String word : arr) {
int sz = word.length();
if (start + sz > n) continue;
String temp = s.substring(start, start + sz);
if (temp.equals(word)) {
if (start + sz == n) flag = true;
else flag = flag || wordBreak(start + sz, s, arr, dp);
}
if (flag) break;
}
dp[start] = flag ? 1 : 0;
return flag;
}
public static void main(String[] args) {
String s = "favtutor";
List<String> v = Arrays.asList("tut", "fav", "o", "r", "ot");
// dp array for memorizing.
int[] dp = new int[s.length() + 2];
Arrays.fill(dp, -1);
System.out.println(wordBreak(0, s, v, dp) ? "True" : "False");
}
}Python Code
Here is the proper Python implementation:
def word_break(start, s, arr, dp):
if dp[start] >= 0:
return dp[start] == 1
n = len(s)
flag = False
for word in arr:
sz = len(word)
if start + sz > n:
continue
temp = s[start:start + sz]
if temp == word:
if start + sz == n:
flag = True
else:
flag = flag or word_break(start + sz, s, arr, dp)
if flag:
break
dp[start] = 1 if flag else 0
return flag
if __name__ == "__main__":
s = "favtutor"
v = ["tut", "fav", "o", "r", "ot"]
# dp array for memorizing.
dp = [-1] * (len(s) + 2)
print("True" if word_break(0, s, v, dp) else "False")Output:
TrueThe time complexity for the above code is O(n*m). Where n is the size of the string and m is the size of the array given to you. As we are iterating over each index of the string and while iterating we are checking for each word present in the array. The space complexity is reduced to O(n) as we are not storing the array values in the hash map.
Let’s compare both approaches in the end:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n*n) | O(n*n) | We are storing the values in the 2D- array which is laid to the space complexity of O(n*n). |
| Optimized | O(n*m) | O(n) | We are checking at each index if any substring forms a word that lies in the array. |
Conclusion
In this article, we see various approaches to solving the Word Break leetcode problem. It helps us to determine which approach is best by time and space complexity. We can also see how calling the loop inside the function reduced our time complexity.