A subarray is a continuous sequence of an array and a lot of algorithms like Kadane’s algorithm, sliding window, etc. help to determine the maximum sum of the subarray or to find the sum of the maximum k-length subarray, etc. In this article, we will discuss the Maximum product Subarray problem with implementation in C++, Java, and Python.
Maximum Product Subarray Problem
In the Maximum Product Subarray problem, we are given an array and we have to find a subarray such that the product of all the elements in that subarray will be the largest.
For example:
INPUT: -1, 2, 3, -2
OUTPUT: 12 ( -1 * 2 * 3 * -2)
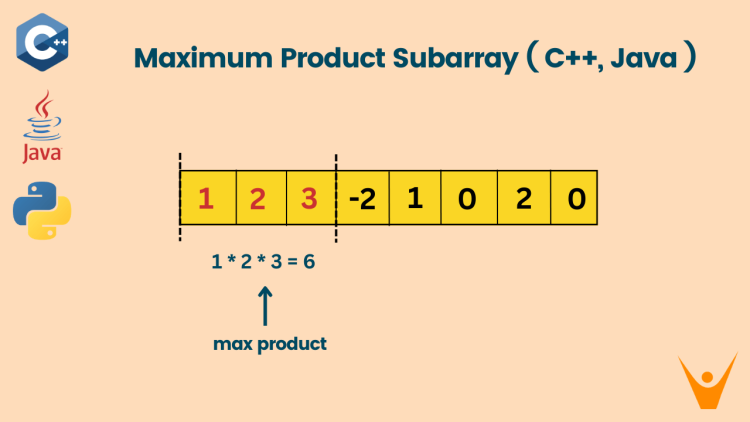
INPUT: 1, 2, 3,- 2
OUTPUT: 6 ( 1 * 2 * 3)
The basic or naive approach is to find all the subarrays and then find which among them have the largest product. Let’s see step by step solution.
- Create a loop of size n
- Create another loop starting from the index of the previous loop.
- Now find the product of the given subarray and compare it with the max value.
- If it is greater than max variable update max to this new product.
- Return the max element.
The time complexity for the above process is O(n*n). Where n is the size of the array. We are iterating two loops to generate all the subarrays. The space complexity for the above code is O(1) as we are not using any extra space.
Optimized Approach for Maximum Product Subarray
In the above approach, the time complexity is huge is can be reduced if we use the concept of Kadane’s algorithm. In this, we will first traverse the array from the left side and find its maximum value then traverse the array from the right side and find its maximum value. Return the maximum value among both of them.
We are doing this as we know if we have a negative value the maximum product either lies on the left side or right. But if we have two negative values, the product will be positive only.
Let’s understand this step by step:
- First, create a variable large that stores the maximum value.
- Now create another variable curr that keeps track of the current product of the subarray. Iterate the loop from left to right and keep updating the curr value by multiplying the current value by curr.
- Update the large to a maximum value of curr and mx.
- Repeat the above two steps from the right to the left side.
- Return the large value.
Let’s Examine the code for the above process.
C++ Code
Below is the C++ program to find Maximum Product Subarray:
#include<bits/stdc++.h>
using namespace std;
int find_max(vector<int>&arr){
int large = INT_MIN;
int curr = 1;
// left iteration
for(int i=0;i<arr.size();i++){
curr = curr*arr[i];
large = max(large, curr);
if(curr==0) curr=1;
}
curr = 1;
// right iteration
for(int i=arr.size()-1;i>=0;i--){
curr = curr*arr[i];
large = max(large, curr);
if(curr==0) curr=1;
}
// return the largest value
return large;
}
int main(){
vector<int>arr = {1, 0, -1, 2, 3};
int and = find_max(arr);
cout<<"maximum product of subarray is: "<<ans<<endl;
return 0;
}Java Code
You can implement it in Java also:
import java.util.*;
class MaximumProductSubarray {
static int findMax(ArrayList<Integer> arr) {
int large = Integer.MIN_VALUE;
int curr = 1;
// Left iteration
for (int i = 0; i < arr.size(); i++) {
curr *= arr.get(i);
large = Math.max(large, curr);
if (curr == 0) curr = 1;
}
curr = 1;
// Right iteration
for (int i = arr.size() - 1; i >= 0; i--) {
curr *= arr.get(i);
large = Math.max(large, curr);
if (curr == 0) curr = 1;
}
// Return the largest value
return large;
}
public static void main(String[] args) {
ArrayList<Integer> arr = new ArrayList<>(Arrays.asList(1, 0, -1, 2, 3));
int ans = findMax(arr);
System.out.println("Maximum product of subarray is: " + ans);
}
}Python Code
Here is the Python program for the optimized approach:
def find_max(arr):
large = float('-inf')
curr = 1
# Left iteration
for num in arr:
curr *= num
large = max(large, curr)
if curr == 0:
curr = 1
curr = 1
# Right iteration
for i in range(len(arr) - 1, -1, -1):
curr *= arr[i]
large = max(large, curr)
if curr == 0:
curr = 1
# Return the largest value
return large
if __name__ == "__main__":
arr = [1, 0, -1, 2, 3]
ans = find_max(arr)
print("Maximum product of subarray is:", ans)Output:
Maximum product of subarray is: 6The time complexity for the above-optimized approach to finding the maximum product array is O(n) where n is the size of the array. As we are just iterating two loops whose total time complexity is 2*O(n) the overall time complexity becomes O(n). The space complexity will remain the same i.e. O(1).
Here is a comparison of how much better is the optimized approach:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n*n) | O(1) | We are finding all the subarrays of the given array which laid time complexity to O(n*n). |
| Optimized Approach | O(n) | O(1) | We are just iterating the loop two times one to find value from left to right and another from right to left. |
Conclusion
In this article, we explore many ways to find the maximum product of the subarray, a famous leetcode problem. Through careful analysis of all the approaches, we find the most efficient way to do it in O(n) time complexity.