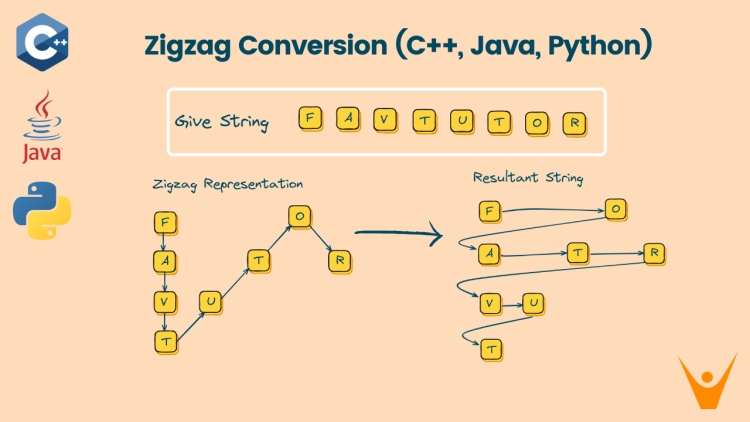
Pattern questions are complex; that’s why they are asked in lots of coding interviews. For example, create a triangle with the use of the ‘*’ symbol, print a string in a zigzag way, etc. All these types of questions need a basic understanding of any programming language. In this article, we will discuss the problem of “Zigzag Conversion”.
What is the Zigzag Conversion problem?
In the ZigZag Conversion problem, you have been given a string that is written in a zigzag way with a given number of rows in it.
Brute Force: Using Array
In this approach, we will create an array of size rows and push characters into the array according to their respective row number. Once we have stored all the characters in the array, we will iterate the array and create a string from it.
Let’s examine the approaches one by one:
- First, create a vector of vector, of size = number of rows. It is used to store the characters of the string.
- Now, create a Boolean variable flag that takes care of the direction in which we are moving, either upward or downward.
- Create another variable j that takes care of the current row.
- Now iterate over the string and check if we reached the 1st row or not. If it is the 1st row, change flag = false, which means we are now moving downward.
- If we are at the last row, change flag = true which means we are now moving upward.
- Store the character in the vector in their respective row.
- At last, check if flag = true then decrease the j = j-1. Otherwise, increase j = j+1.
- Now iterate over the vector row by row and store and append each row character into the resultant string.
The time complexity for the above approach is O(n), where n is the size of the string. As we are iterating over the string once which takes O(n) time complexity. The space complexity is O(n) as we are storing each character of the string into a vector.
Optimized Approach
In the above approach, we are taking extra space. To reduce that extra space we will directly store that character in the resultant string instead of storing it first into the vector. This can be achieved with a simple observation.
All the characters that are present in the 1st and the last row will be (2*n)-2 distance apart from their neighboring characters. All the characters present other than these rows will repeat them after (2*(n-j) – 2) if we are moving downward and (2*j) if we are moving upward.
Let’s examine this approach step by step.
- Create a resultant string res. Now create a variable j which takes care of the current index.
- Iterate over the rows and check if we are at the 1st or last row. Then, we update our current index with j = j + (2*n-2). Keep iterating till j < size of the string.
- If we are at any other row, then update our current index with j = j + (2*(n-j)-2) if the flag is true. Otherwise, update the index with j = j + (2*j). Keep iterating till j < size of the string.
- Keep adding the characters of the current index into the resultant string.
- Return the resultant string at last.
Let’s examine the code for the above approach.
C++ Code
Here is how you can implement the Optimized Approach in C++:
#include<bits/stdc++.h>
using namespace std;
string zigzag_conversion(string s, int n){
if(n <= 1) return s;
string res = "";
int j = 0, sz = s.size();
for(int i=0;i<n;i++){
bool flag = true;
j = i;
while(j<sz){
res+= s[j];
if(i == 0 || i == n-1){
j += (2*n)-2;
}
else{
if(flag){
j += (2*(n-i))-2;
}else{
j += (2*i);
}
flag = !flag;
}
}
}
return res;
}
int main(){
string s = "FAVTUTOR";
int n = 4;
string ans = zigzag_conversion(s, n);
cout<<"Resultant string is: "<<ans<<endl;
return 0;
}Java Code
Here is the same solution in Java:
class ZigzagConversion {
public static String zigzagConversion(String s, int n) {
if (n <= 1) return s;
StringBuilder res = new StringBuilder();
int j = 0, sz = s.length();
for (int i = 0; i < n; i++) {
boolean flag = true;
j = i;
while (j < sz) {
res.append(s.charAt(j));
if (i == 0 || i == n - 1) {
j += (2 * n) - 2;
} else {
if (flag) {
j += (2 * (n - i)) - 2;
} else {
j += (2 * i);
}
flag = !flag;
}
}
}
return res.toString();
}
public static void main(String[] args) {
String s = "FAVTUTOR";
int n = 4;
String ans = zigzagConversion(s, n);
System.out.println("Resultant string is: " + ans);
}
}Python Code
You can implement in Python also:
def zigzag_conversion(s, n):
if n <= 1:
return s
res = ""
j = 0
sz = len(s)
for i in range(n):
flag = True
j = i
while j < sz:
res += s[j]
if i == 0 or i == n - 1:
j += (2 * n) - 2
else:
if flag:
j += (2 * (n - i)) - 2
else:
j += 2 * i
flag = not flag
return res
if __name__ == "__main__":
s = "FAVTUTOR"
n = 4
ans = zigzag_conversion(s, n)
print("Resultant string is:", ans)Output:
Resultant srting is: FOATRVUTThe time complexity for the above code is O(n) as we are just iterating the string once, which takes O(n) time complexity. The space complexity is O(1) as we are not using any extra space because we are directly storing the characters into the resultant string.
Here’s the difference between both approaches:
| Analysis | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n) | O(n) | We are using extra space to first store the characters in their respective rows. Then, using those rows, we will create a string. |
| Optimized | O(n) | O(1) | We are storing the values directly into the resultant string. |
Conclusion
In this article, we see various ways to solve the “Zigzag Conversion” problem. We had seen that we can store the characters in their respective rows and then for the resultant string from them. But we are using extra space to store the characters, which can be reduced if we iterate the string row-wise instead of column-wise. There are some more questions on patterns like “Longest Palindromic Substring,” “Valid Parentheses,” etc. Try to solve these questions on your own to clear your fundamentals.