In the world of computer programming, word search puzzles have always been a popular and challenging game to solve. The task of finding words in a grid of letters has fascinated both enthusiasts and developers alike. In this article, we will explore the concept of word search, and discuss an approach to solve the ‘word search II’ leetcode problem.
What is the Word Search II Problem?
The goal of the classic problem word search II is to locate a list of given words that are hidden within a grid of letters. The words can be spelled forward or backward and arranged horizontally, vertically, or diagonally. Each letter in the grid can only be used once to form a word, the main task is to identify words from a jumble of letters and mark them as found.
Let us take an example to understand clearly:
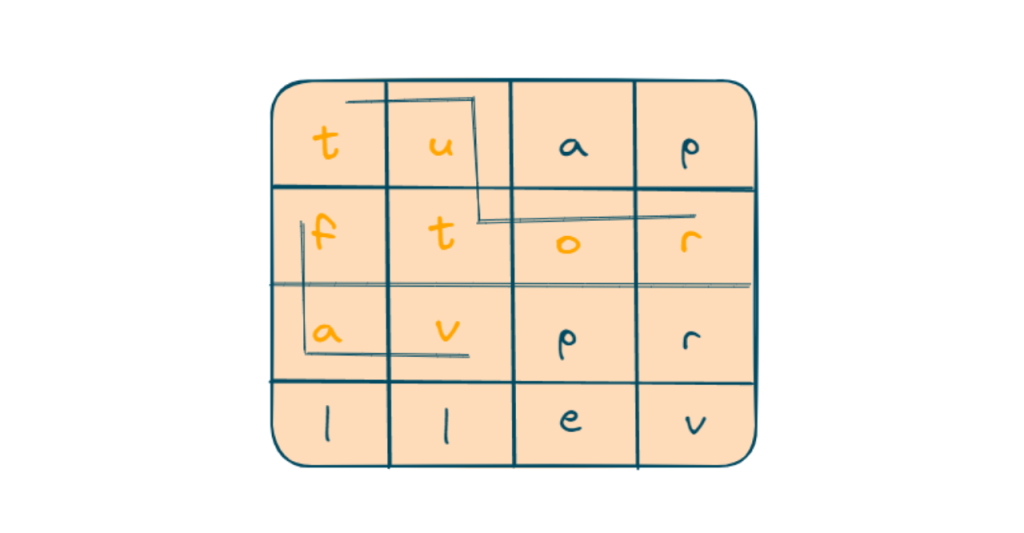
Input:
words = [“fav”, “tutor”, “pear”]
board = [
[‘t’, ‘u’, ‘a’, ‘p’],
[‘f’, ‘t’, ‘o’, ‘r’ ],
[‘a’, ‘v’, ‘p’, ‘r’],
[‘l’, ‘l’, ‘e’, ‘v’ ] ]
Output:
[“fav”, “tutor”]
In this example, we have a 2D board and a list of words. The task is to find all the words from the list that can be constructed using the letters on the board. In this case, the words “fav” and “tutor” can be found on the board.
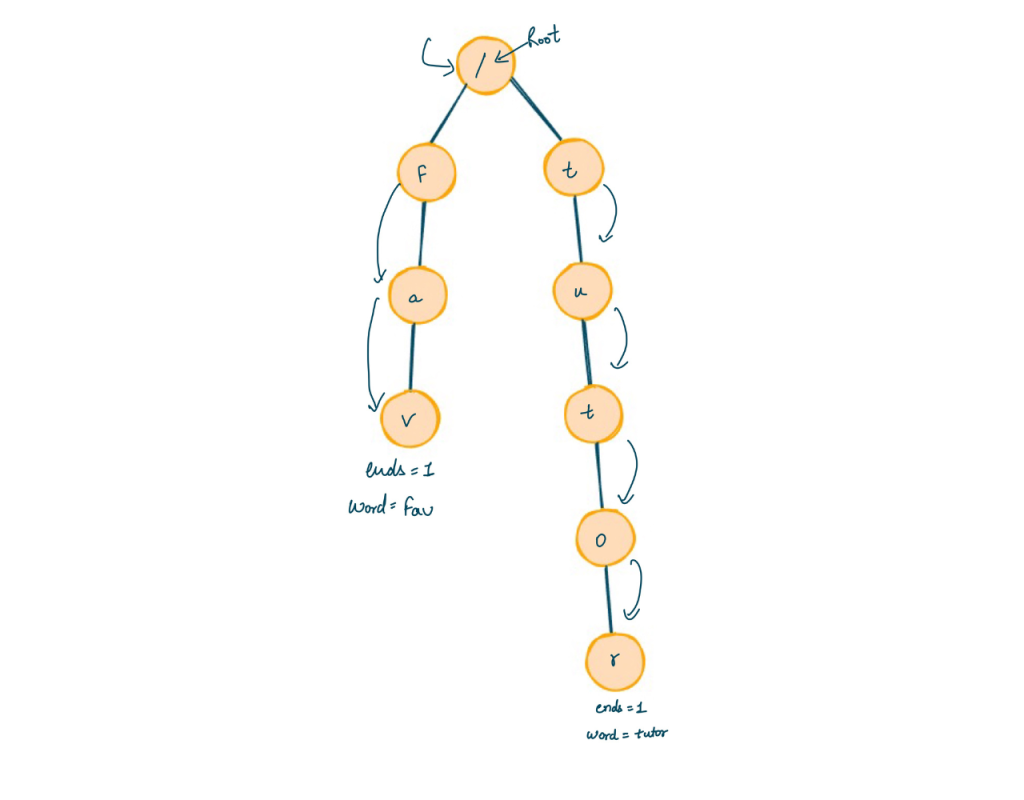
Backtracking Approach: Using Trie
Solving the Word Search II problem using backtracking efficiently involves using the Trie data structure to store the list of words. The Trie data structure allows us to build a hierarchical representation of the list words. Each node in the Trie represents a letter, and the paths from the root to the nodes form words.
We will follow the given steps to solve this problem:
- Create a Trie data structure and insert all the words from the list into the Trie.
- Iterate over each cell in the 2D board and perform a depth-first search (DFS) starting from that cell.
- In the DFS, check if the current letter in the board exists in the Trie. If it does, move to the next letter and continue the DFS recursively.
- If we reach a node in the Trie that represents the end of a word, add that word to the result list.
- Keep track of visited cells to avoid reusing the same letter in a word.
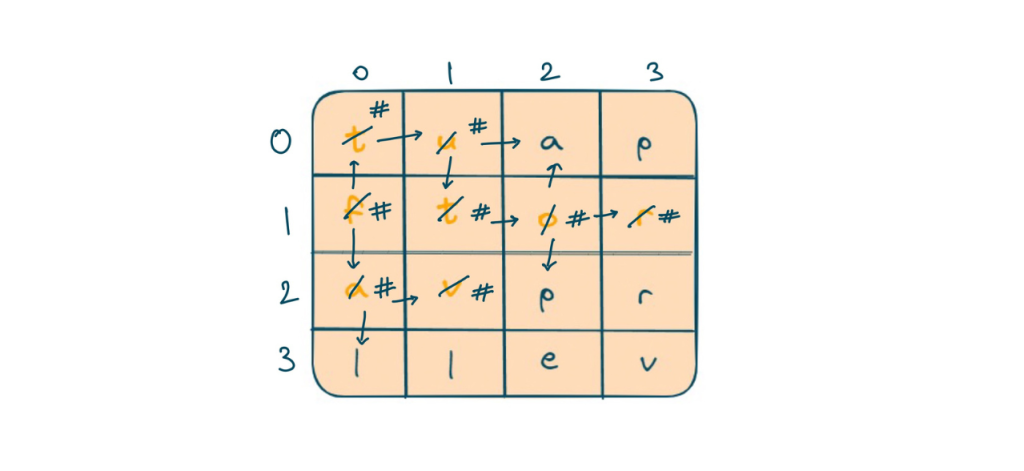
- Repeat the DFS for each cell on the board.
- After completing the DFS for a cell, mark it as unvisited to allow other paths to use it.
C++ Code
Below is the C++ program to solve Word Search II problem:
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
class TrieNode {
public:
unordered_map<char, TrieNode*> children;
bool isEnd;
TrieNode() : isEnd(false) {}
};
class Trie {
public:
TrieNode* root;
Trie() : root(new TrieNode()) {}
void insert(const string& word) {
TrieNode* node = root;
for (char c : word) {
if (!node->children.count(c)) {
node->children[c] = new TrieNode();
}
node = node->children[c];
}
node->isEnd = true;
}
};
class Solution {
public:
vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
Trie trie;
for (const string& word : words) {
trie.insert(word);
}
vector<string> result;
int m = board.size();
int n = board[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
dfs(board, trie.root, i, j, "", result);
}
}
return result;
}
private:
void dfs(vector<vector<char>>& board, TrieNode* node, int i, int j, string path, vector<string>& result) {
char c = board[i][j];
if (!node->children.count(c)) {
return; // Stop DFS if the current path is not a prefix of any word
}
node = node->children[c];
if (node->isEnd) {
result.push_back(path + c);
node->isEnd = false; // Remove the word from the Trie to avoid duplicates
}
board[i][j] = '#'; // Mark the cell as visited
// Explore neighbors in all directions
static const vector<pair<int, int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (const auto& dir : directions) {
int ni = i + dir.first;
int nj = j + dir.second;
if (ni >= 0 && ni < board.size() && nj >= 0 && nj < board[0].size() && board[ni][nj] != '#') {
dfs(board, node, ni, nj, path + c, result);
}
}
board[i][j] = c; // Restore the cell to its original state
}
};
int main() {
Solution solution;
vector<string> words = {"fav", "tutor", "pear"};
vector<vector<char>> board = {
{'t', 'u', 'a', 'p'},
{'f', 't', 'o', 'r'},
{'a', 'v', 'p', 'r'},
{'l', 'l', 'e', 'v'}
};
vector<string> result = solution.findWords(board, words);
cout << "Output: [";
for (int i = 0; i < result.size(); ++i) {
cout << "\"" << result[i] << "\"";
if (i < result.size() - 1) {
cout << ", ";
}
}
cout << "]" << endl;
return 0;
}Python Code
Below is the Python program to solve the Word Search II problem:
from typing import List
class TrieNode:
def __init__(self):
self.children = {}
self.isEnd = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
node = self.root
for c in word:
if c not in node.children:
node.children[c] = TrieNode()
node = node.children[c]
node.isEnd = True
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
trie = Trie()
for word in words:
trie.insert(word)
result = []
m, n = len(board), len(board[0])
def dfs(node, i, j, path):
nonlocal board, result
if i < 0 or i >= m or j < 0 or j >= n or board[i][j] == '#' or board[i][j] not in node.children:
return
char = board[i][j]
node = node.children[char]
if node.isEnd:
result.append(path + char)
node.isEnd = False # Remove the word from the Trie to avoid duplicates
board[i][j] = '#' # Mark the cell as visited
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for x, y in directions:
ni, nj = i + x, j + y
dfs(node, ni, nj, path + char)
board[i][j] = char # Restore the cell to its original state
for i in range(m):
for j in range(n):
dfs(trie.root, i, j, "")
return result
if __name__ == "__main__":
solution = Solution()
words = ["fav", "tutor", "pear"]
board = [
['t', 'u', 'a', 'p'],
['f', 't', 'o', 'r'],
['a', 'v', 'p', 'r'],
['l', 'l', 'e', 'v']
]
result = solution.findWords(board, words)
print("Output:", result)Java Code
Below is the Java program to solve it:
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
class TrieNode {
Map<Character, TrieNode> children;
boolean isEnd;
TrieNode() {
children = new HashMap<>();
isEnd = false;
}
}
class Trie {
TrieNode root;
Trie() {
root = new TrieNode();
}
void insert(String word) {
TrieNode node = root;
for (char c : word.toCharArray()) {
if (!node.children.containsKey(c)) {
node.children.put(c, new TrieNode());
}
node = node.children.get(c);
}
node.isEnd = true;
}
}
public class WordSearchII {
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
List<String> result = new ArrayList<>();
int m = board.length;
int n = board[0].length;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
dfs(board, trie.root, i, j, "", result);
}
}
return result;
}
private void dfs(char[][] board, TrieNode node, int i, int j, String path, List<String> result) {
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] == '#' || !node.children.containsKey(board[i][j])) {
return;
}
char c = board[i][j];
node = node.children.get(c);
if (node.isEnd) {
result.add(path + c);
node.isEnd = false; // Remove the word from the Trie to avoid duplicates
}
board[i][j] = '#'; // Mark the cell as visited
int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (int[] dir : directions) {
int ni = i + dir[0];
int nj = j + dir[1];
dfs(board, node, ni, nj, path + c, result);
}
board[i][j] = c; // Restore the cell to its original state
}
public static void main(String[] args) {
WordSearchII wordSearch = new WordSearchII();
String[] words = {"fav", "tutor", "pear"};
char[][] board = {
{'t', 'u', 'a', 'p'},
{'f', 't', 'o', 'r'},
{'a', 'v', 'p', 'r'},
{'l', 'l', 'e', 'v'}
};
List<String> result = wordSearch.findWords(board, words);
System.out.print("Output: [");
for (int i = 0; i < result.size(); ++i) {
System.out.print("\"" + result.get(i) + "\"");
if (i < result.size() - 1) {
System.out.print(", ");
}
}
System.out.println("]");
}
}Output:
Output: ["tutor", "fav"]Complexity Analysis
Let’s look at the time and space complexity of the same.
For each word in the words array, the code inserts it into the Trie. The insertion operation takes O(L) time, where L is the length of the word.
- If there are N words and the average length of words is M, the total time complexity for inserting all words into the Trie is O(N * M).
- The code performs a Depth-First Search (DFS) on the board starting from each cell. In the worst case, it explores all possible paths on the board.
- For each cell, the DFS explores four neighboring cells (up, down, left, right).
Therefore, the DFS can take up to O(4^(m*n)) (m&n are board dimensions) time in the worst case.
Total Time Complexity is O(4^(m*n)).
- The space required for the Trie depends on the number and length of words. In the worst case, where there are N words with an average length of M, the space complexity is O(N * M).
- The DFS is performed recursively, and the maximum depth of recursion is the maximum possible path length on the board.
- The maximum depth is O(m * n) in the worst case (when exploring all cells on the board)
The overall space complexity is dominated by the Trie, so it is O(N * M).
Conclusion
In this article, we explored the concept of word search II problem from leetcode and discussed an optimized approach to solve this problem using a trie data structure. The Trie approach leverages the hierarchical structure of the Trie to perform fast searches and provides an elegant solution to the word search II problem.








