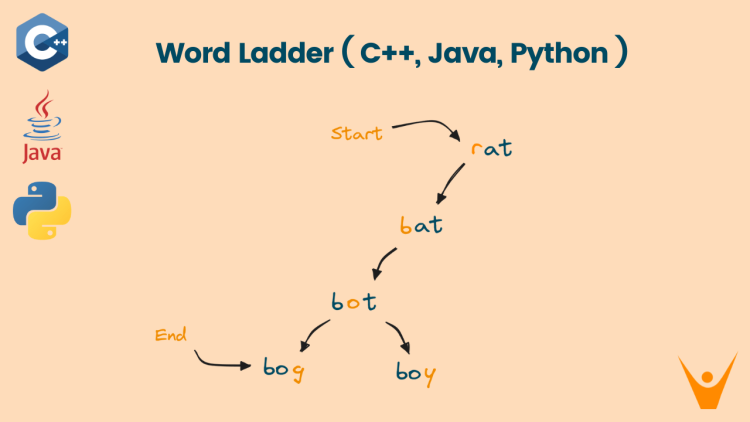
The word ladder is one of the problems that involves creative thinking. In this article, you will come to know about an approach to solving the word ladder problem, analyze their time and space complexity, and provide the solution in C++, Java, and Python.
What is the Word Ladder Problem?
The word ladder is the problem that involves finding the shortest word transformation from a given start word to a target word. Each transformation involves Transforming one word to another by changing only one letter at a time and each transformed word must exist in a provided word list.
For example:
Start Word = “rat”
End Word = “bog”
Word List = { “bat”, “boy”, “bot”, “bog” }
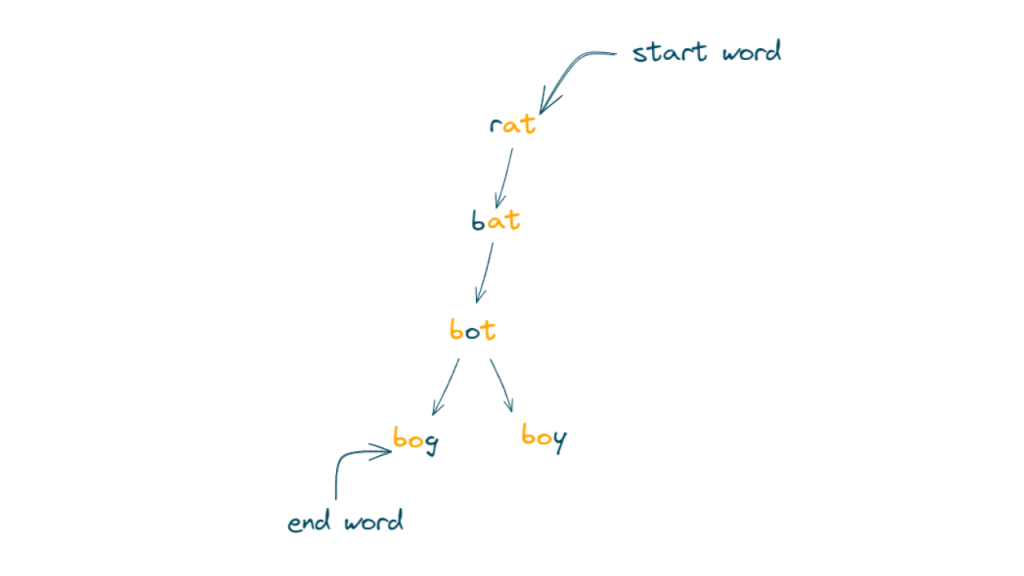
The shortest word transformation from “rat” to “bog” in the given word list is 4, and the sequence is “rat” -> “bat” -> “bot” –> “bog”. Note that the word “boy” was present in the word list but was not a valid transformation in this case.
BFS Traversal Approach to Solve Word Ladder
The breadth-first search (BFS) approach is an efficient approach to solving the World Ladder problem. BFS explores all possible word transformations while keeping track of the shortest path to reach the ending word. The BFS algorithm starts with the starting word, explores its neighboring words, and continues the process until it reaches the ending word.
Start with declaring a queue to store BFS traversal and a HashSet to check whether a new word was present in the word list or not. The hashset is used to reduce the time complexity.
Let’s understand it better with an example.
Step: 1 Enqueue the start word “rat” with a transformation length of 1, and Initialise the word set to [“bat”, “boy”, “bot”, “bog”].
Step: 2 Dequeue “rat” (transformation length = 1). The key step involves generating one-letter transformations from the current word by changing the letter “r” to each letter from ‘a’ to ‘z’ and selecting words present in the word list.
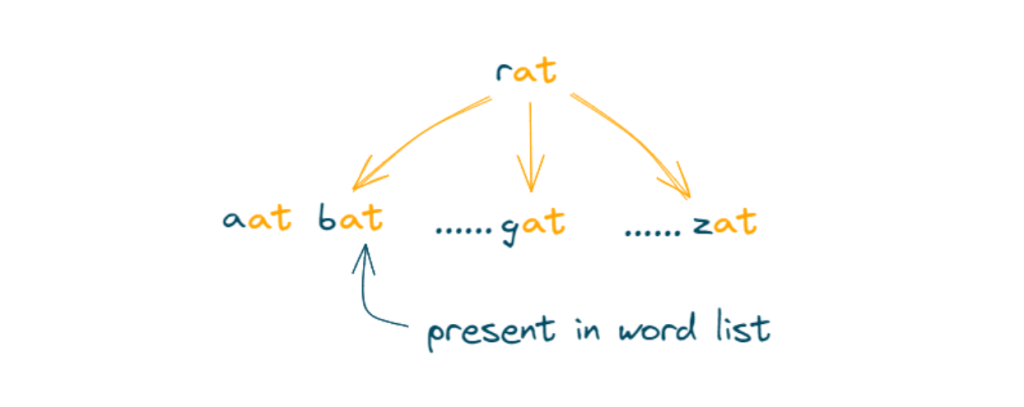
Since “bat” is present in the list, we can transform “rat” to “bat”.
Now, Enqueue “bat” with a transformation length of 2, and mark “bat” as visited by removing it from the word set.
Step: 3 Dequeue “bat” (transformation length = 2).
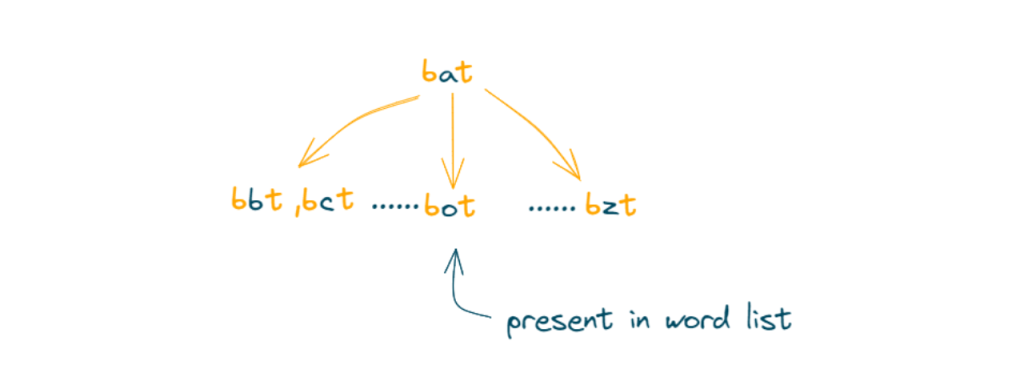
Generate one-letter transformations: “bat” (ignore, as it’s the same as the current word), “bot”.
Enqueue “bot” with a transformation length of 3, and mark “bot” as visited by removing it from the word set.
Step: 4 Dequeue “bot” (transformation length = 3).
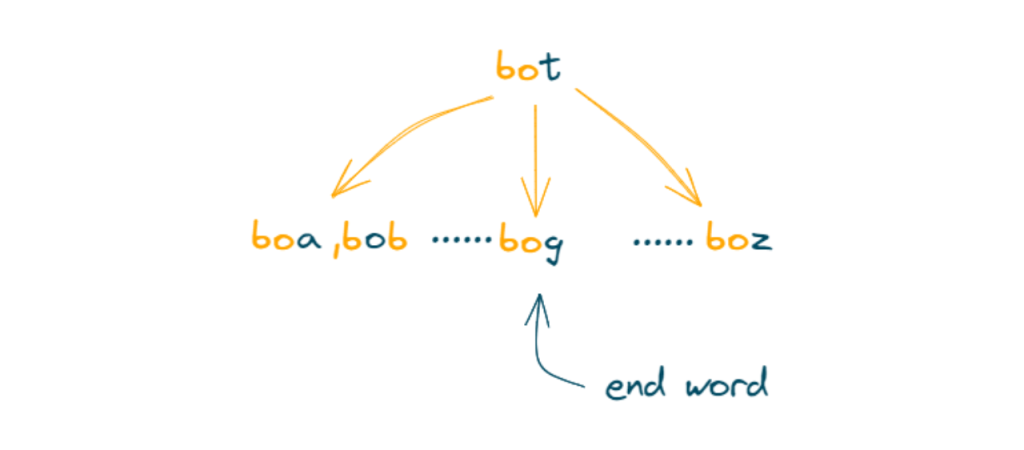
Generate one-letter transformations: “bot” (ignore), “bat” (ignore), “hot”, …, “bot” (ignore).
Enqueue “bog” with a transformation length of 4. Mark “bog” as visited by removing it from the word set.
Step: 5 Dequeue “bog” (transformation length = 4).
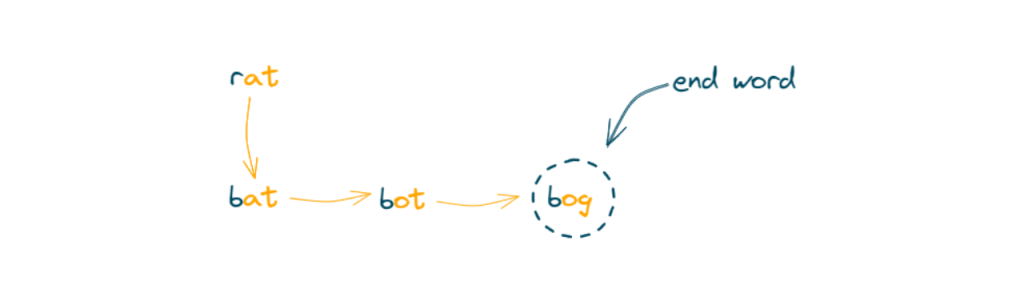
The target word “bog” is reached, and the transformation length is 4.
Return the transformation length, which is 4.
C++ Code
Here is the C++ program to solve the Word Ladder problem:
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_set>
using namespace std;
class Solution {
public:
int wordLadderLength(string startword, string targetword, vector<string>& wordlist) {
queue<pair<string, int>> q;
q.push({startword, 1});
// Using an unordered_set for O(1) word existence check and removal
unordered_set<string> st(wordlist.begin(), wordlist.end());
// Remove the start word from the set
st.erase(startword);
while (!q.empty()) {
string word = q.front().first;
int steps = q.front().second;
q.pop();
if (word == targetword) {
return steps;
}
// Generate one-letter transformations of the current word
for (int i = 0; i < word.size(); i++) {
char original = word[i];
for (char ch = 'a'; ch <= 'z'; ch++) {
word[i] = ch;
if (st.find(word) != st.end()) {
// If the transformed word is in the set, remove it and enqueue
st.erase(word);
q.push({word, steps + 1});
}
}
// Restore the original character at position I
word[i] = original;
}
}
// If no transformation found
return 0;
}
};
int main() {
Solution solution;
string startWord = "rat";
string endWord = "bog";
vector<string> wordList = {"bat", "boy", "bot", "bog"};
int result = solution.wordLadderLength(startWord, endWord, wordList);
if (result > 0) {
cout << "Shortest word ladder length: " << result << endl;
}
else {
cout << "No transformation sequence found." << endl;
}
return 0;
}Python Code
Below is the Python program for the BFS approach to solve Word Ladder problem:
from collections import deque
class Solution:
def word_ladder_length(self, start_word, target_word, word_list):
q = deque([(start_word, 1)])
st = set(word_list)
# Remove the start word from the set
st.discard(start_word)
while q:
word, steps = q.popleft()
if word == target_word:
return steps
# Generate one-letter transformations of the current word
for i in range(len(word)):
original = word[i]
for ch in 'abcdefghijklmnopqrstuvwxyz':
# Generate a new word
new_word = word[:i] + ch + word[i+1:]
if new_word in st:
# If the transformed word is in the set, remove it and enqueue
st.remove(new_word)
q.append((new_word, steps + 1))
# Restore the original character at position i
word = word[:i] + original + word[i+1:]
# If no transformation found
return 0
if __name__ == "__main__":
solution = Solution()
start_word = "rat"
end_word = "bog"
word_list = ["bat", "boy", "bot", "bog"]
result = solution.word_ladder_length(start_word, end_word, word_list)
if result > 0:
print("Shortest word ladder length:", result)
else:
print("No transformation sequence found.")
Java Code
You can the Java program below for Word Ladder:
import java.util.*;
class Solution {
public int wordLadderLength(String startWord, String targetWord, List<String> wordList) {
Queue<Map.Entry<String, Integer>> q = new LinkedList<>();
q.offer(new AbstractMap.SimpleEntry<>(startWord, 1));
Set<String> wordSet = new HashSet<>(wordList);
// Remove the start word from the set
wordSet.remove(startWord);
while (!q.isEmpty()) {
Map.Entry<String, Integer> current = q.poll();
String word = current.getKey();
int steps = current.getValue();
if (word.equals(targetWord)) {
return steps;
}
// Generate one-letter transformations of the current word
for (int i = 0; i < word.length(); i++) {
char[] chars = word.toCharArray();
char original = chars[i];
for (char ch = 'a'; ch <= 'z'; ch++) {
chars[i] = ch;
String transformedWord = new String(chars);
if (wordSet.contains(transformedWord)) {
// If the transformed word is in the set, remove it and enqueue
wordSet.remove(transformedWord);
q.offer(new AbstractMap.SimpleEntry<>(transformedWord, steps + 1));
}
}
// Restore the original character at position i
chars[i] = original;
}
}
// If no transformation found
return 0;
}
public static void main(String[] args) {
Solution solution = new Solution();
String startWord = "rat";
String endWord = "bog";
List<String> wordList = Arrays.asList("bat", "boy", "bot", "bog");
int result = solution.wordLadderLength(startWord, endWord, wordList);
if (result > 0) {
System.out.println("Shortest word ladder length: " + result);
} else {
System.out.println("No transformation sequence found.");
}
}
}Output:
Shortest word ladder length: 4Complexity Analysis
The time complexity of the Word Ladder solution is O(N * M * 26), where N represents the size of the word list array, and M denotes the word length of the words present in the word list. It’s important to note that the constant factor 26 is attributed to the number of characters in the alphabet.
The space complexity is O(N), encompassing the creation of an unordered set and the storage of all values from the wordList array. This space complexity accounts for the memory required for efficient traversal and storage during the execution of the algorithm.
Conclusion
In summary, the Word Ladder problem is a creative challenge with practical applications in natural language processing, spell check and autocorrection systems, and genetic algorithms. We used the BFS traversal approach to solve this problem with the time complexity O(N * M * 26), where N is the size of the word list, and M is the word length.