We know that Sudoku is a popular puzzle game that requires players to fill a 9×9 grid with numbers from 1 to 9. This article will discuss an approach, along with examples, to solve this interesting leetcode problem called ‘Valid Sudoku’ to check if the sudoku board configuration is correct or not.
What is the Valid Sudoku Problem?
In the Valid Sodoku problem, we are given a 9×9 sudoku board, our goal is to check whether it is valid or not. The objective is to ensure that each row, column, and 3×3 sub-grid contains all the digits from 1 to 9 without repetition.
A valid sudoku must follow the 3 following conditions:
- Each row must contain the digits 1 to 9 without repetition.
- Each column must contain the digits 1 to 9 without repetition.
- Each 3×3 sub-grid must contain the digits 1 to 9 without repetition.
We have to consider only the filled value in the grid to check the validity.
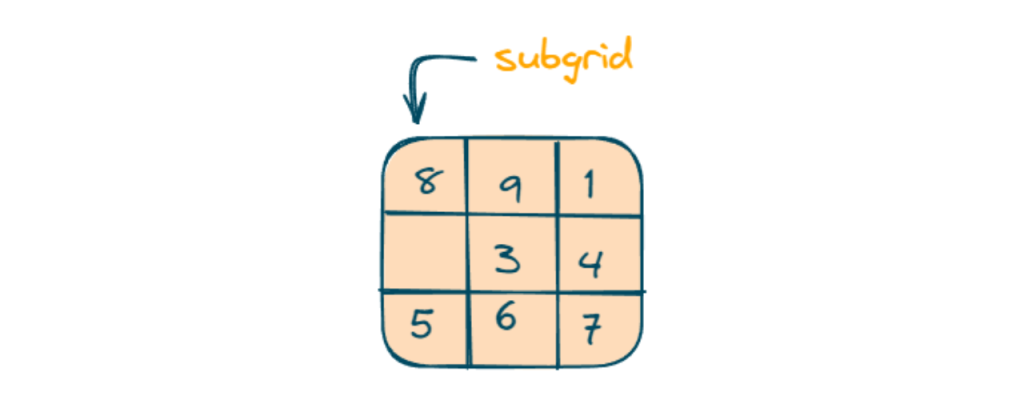
Let us understand it with an example with this board:
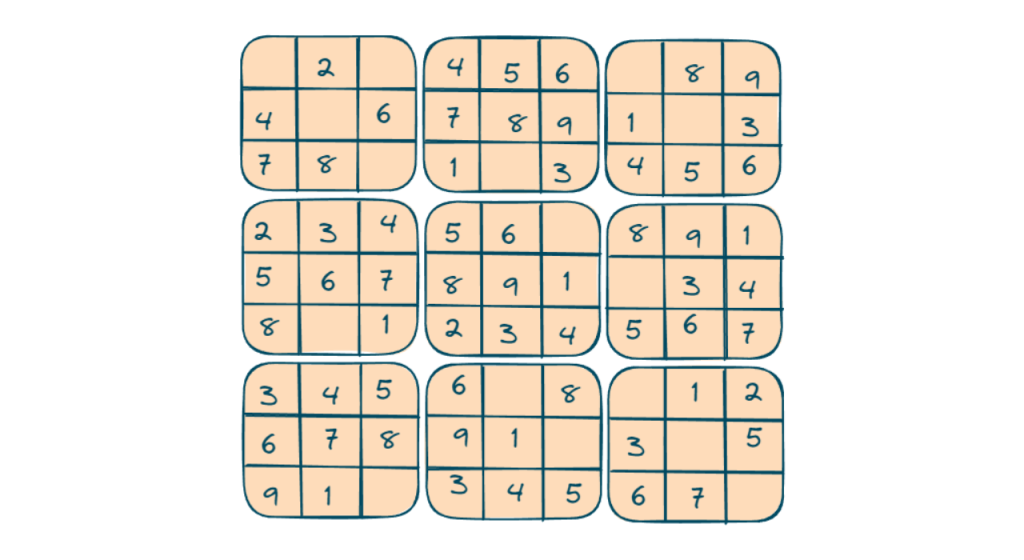
Here are 9 subgrids of 3×3.
Output = valid Because there is no repetition within rows, columns, and subgrids
HashSet to Check Sudoku Configuration is Valid
To solve this problem, we will use a HashSet to check the repetition of numbers within rows, columns, and subgrids.
- We will declare a HashSet of strings to keep track of elements seen during the iteration
- We will run a nested loop and check only for nonempty cells using this condition board[i][j] != ‘ ‘
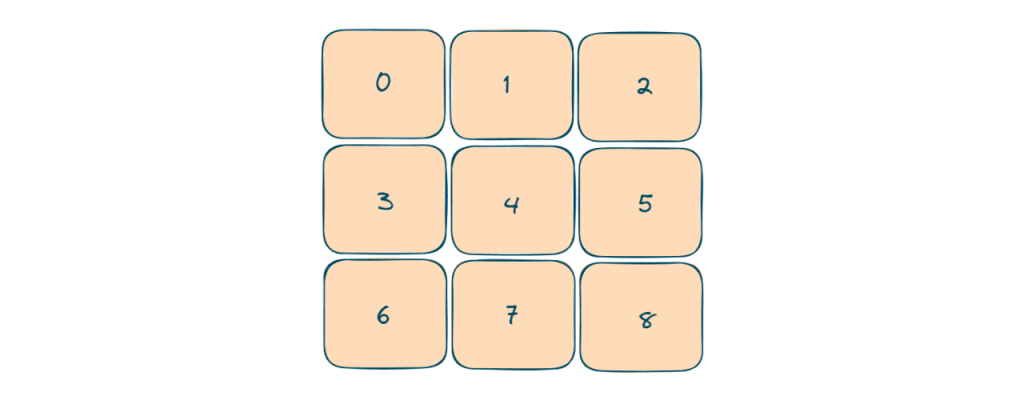
- We will make a string like for row string is “row+i+board[i][j]” (here i is row number), for columns “col+j+board[i][j]” (here j is column number), for box, we will use a formula to obtain box number (i/3)*3+(j/3) and string for the box is “box+(i/3)*3+(j/3)+board[i][j]
- Now we will check if the string of row, column, and box is present in the set then will return false otherwise we will return true. If all iterations run successfully.
C++ Code
Below is the C++ program to solve the Valid Sudoku problem:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
unordered_set<string> seen;
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
if (!seen.insert("row" + to_string(i) + board[i][j]).second ||
!seen.insert("col" + to_string(j) + board[i][j]).second ||
!seen.insert("box" + to_string((i / 3) * 3 + j / 3) + board[i][j]).second) {
return false;
}
}
}
}
return true;
}
};
int main() {
// Example usage:
Solution solution;
vector<vector<char>> board = {
{'.', '2', '.', '4', '5', '6', '.', '8', '9'},
{'4', '.', '6', '7', '8', '9', '1', '.', '3'},
{'7', '8', '.', '1', '.', '3', '4', '5', '6'},
{'2', '3', '4', '5', '6', '.', '8', '9', '1'},
{'5', '6', '7', '8', '9', '1', '.', '3', '4'},
{'8', '.', '1', '2', '3', '4', '5', '6', '7'},
{'3', '4', '5', '6', '.', '8', '.', '1', '2'},
{'6', '7', '8', '9', '1', '.', '3', '.', '5'},
{'9', '1', '.', '3', '4', '5', '6', '7', '.'}
};
bool result = solution.isValidSudoku(board);
cout << (result ? "Valid" : "Invalid") << endl;
return 0;
}Java Code
The implementation is quite similar in Java:
import java.util.HashSet;
class Solution {
public boolean isValidSudoku(char[][] board) {
HashSet<String> seen = new HashSet<>();
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
if (!seen.add("row" + i + board[i][j]) ||
!seen.add("col" + j + board[i][j]) ||
!seen.add("box" + (i / 3) * 3 + j / 3 + board[i][j])) {
return false;
}
}
}
}
return true;
}
public static void main(String[] args) {
Solution solution = new Solution();
char[][] board = {
{'.', '2', '.', '4', '5', '6', '.', '8', '9'},
{'4', '.', '6', '7', '8', '9', '1', '.', '3'},
{'7', '8', '.', '1', '.', '3', '4', '5', '6'},
{'2', '3', '4', '5', '6', '.', '8', '9', '1'},
{'5', '6', '7', '8', '9', '1', '.', '3', '4'},
{'8', '.', '1', '2', '3', '4', '5', '6', '7'},
{'3', '4', '5', '6', '.', '8', '.', '1', '2'},
{'6', '7', '8', '9', '1', '.', '3', '.', '5'},
{'9', '1', '.', '3', '4', '5', '6', '7', '.'}
};
boolean result = solution.isValidSudoku(board);
System.out.println(result ? "Valid" : "Invalid");
}
}Python Code
Here is the Python program as well:
from typing import List
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
seen = set()
for i in range(9):
for j in range(9):
if board[i][j] != '.':
if f"row{i}{board[i][j]}" in seen or \
f"col{j}{board[i][j]}" in seen or \
f"box{(i // 3) * 3 + j // 3}{board[i][j]}" in seen:
return False
seen.add(f"row{i}{board[i][j]}")
seen.add(f"col{j}{board[i][j]}")
seen.add(f"box{(i // 3) * 3 + j // 3}{board[i][j]}")
return True
# Example usage
solution = Solution()
board = [
['.', '2', '.', '4', '5', '6', '.', '8', '9'],
['4', '.', '6', '7', '8', '9', '1', '.', '3'],
['7', '8', '.', '1', '.', '3', '4', '5', '6'],
['2', '3', '4', '5', '6', '.', '8', '9', '1'],
['5', '6', '7', '8', '9', '1', '.', '3', '4'],
['8', '.', '1', '2', '3', '4', '5', '6', '7'],
['3', '4', '5', '6', '.', '8', '.', '1', '2'],
['6', '7', '8', '9', '1', '.', '3', '.', '5'],
['9', '1', '.', '3', '4', '5', '6', '7', '.']
]
result = solution.isValidSudoku(board)
print("Valid" if result else "Invalid")Output:
ValidTo know more about HashSet, we have a detailed guide on Hashing for beginners.
Complexity Analysis
The time complexity of the algorithm is O(N^2), where N is the size of the Sudoku board (N x N) as the algorithm traverses through each cell in the board exactly once, resulting in a nested loop structure iterating over N x N cells.
The space complexity of the algorithm is O(N) due to the usage of additional space for storing sets.
Conclusion
In conclusion, the “valid sudoku” leetcode problem is used to find whether the order of numbers present in the sudoku board is valid or not. It can be efficiently solved using the HashSet.