Arrays play a significant role in the world of programming and there are a lot of interview questions that depend on array data structure. In this article, we will explore different approaches to solving the ‘subarray sum equals k’ problem, starting with the brute force approach and gradually moving towards more efficient solutions using techniques of prefix sums.
What is the Subarray Sum Equals K Problem?
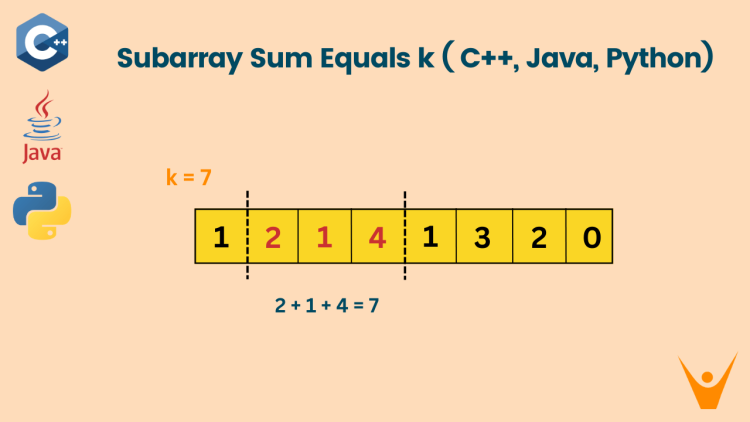
One particular problem that frequently arises is finding subarrays whose sum equals a given number, commonly referred to as the “subarray sum equals k” problem. This problem requires several subarrays with sum k where k is the given target.
In this problem, we are given an array and we have to tell the number of subarrays that sum equals k, a subarray is a contiguous subsequence of an array.
Let us understand it with an example:
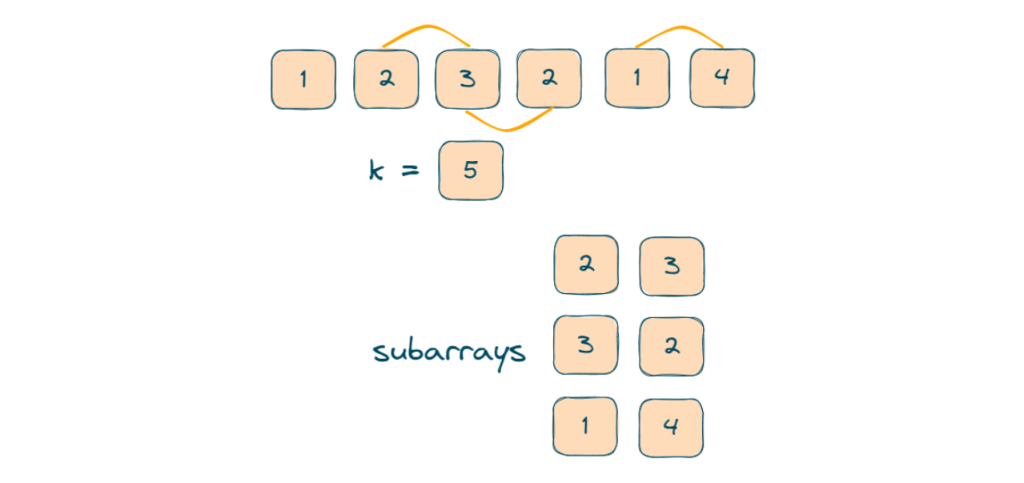
Array = [1,2,3,2,1,4]
k = 5
Output = 3
There are 3 subarrays, i.e. {2,3}, {3,2}, {1,4} whose element’s sum is 5.
Check out Kadane’s Algorithm to learn how to find maximum sum subarray.
Brute Force Approach
In the naive approach, we will generate all possible subarrays and check whether the sum of elements in the array is equal to k or not.
Steps for brute force approach:
- In this approach,
- we will use a nested loop to generate a subarray and inside this nested loop, we will run a loop for the sum of elements.
- We will initialize a count variable initially 0 to count the subarray with the given sum k.
- We will run loop i from 0 to n-1 where n is the size of the array and inside it we will run a loop j from i to n-1.
- i denotes the starting index of the subarray and j denotes the ending index.
- We will add all the elements between index i and j including i,j using another loop.
- When the subarray sum is equal to k we will increment the count variable.
For the above example:
Array = [1,2,3,2,1,4]
k = 5
Output = 3
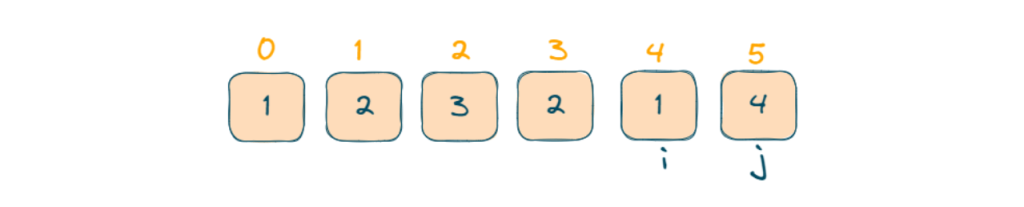
- The subarray with starting index i = 1 to ending index j = 2 has a sum equal to k.
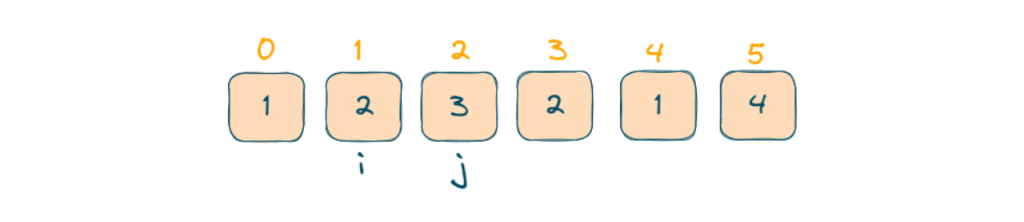
- The subarray with starting index i = 2 to ending index j = 3 has a sum equal to k.
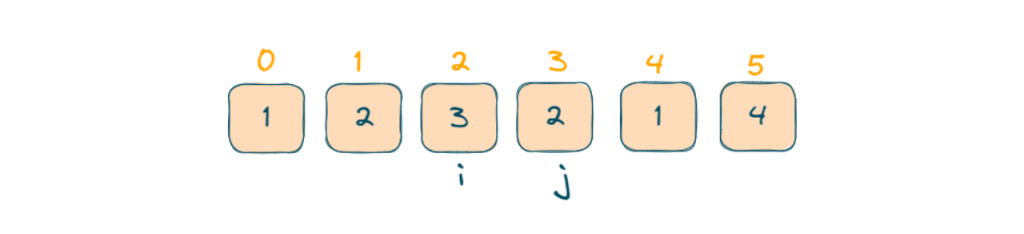
- The subarray with starting index i = 4 to ending index j = 5 has a sum equal to k.
The time complexity for the brute force approach is O(n3) because we are using a nested loop for finding the subarray with sum k and inside the nested loop there is another loop to sum all the elements of the subarray
The space complexity for this approach is O(1) as we have not used any extra space
Optimized Approach: Using Prefix Sum
In this approach, we will use the prefix sum technique to solve this problem. The prefix sum represents the cumulative sum up to the current index.
Steps to solve the problem using the prefix sum approach:
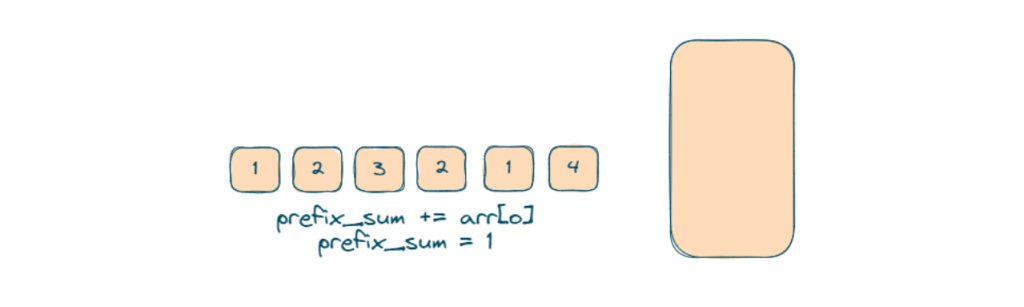
- Firstly we will declare a prefix_sum variable and a hashmap sum_count
- We will use a hashmap that stores the frequency of each prefix sum encountered so
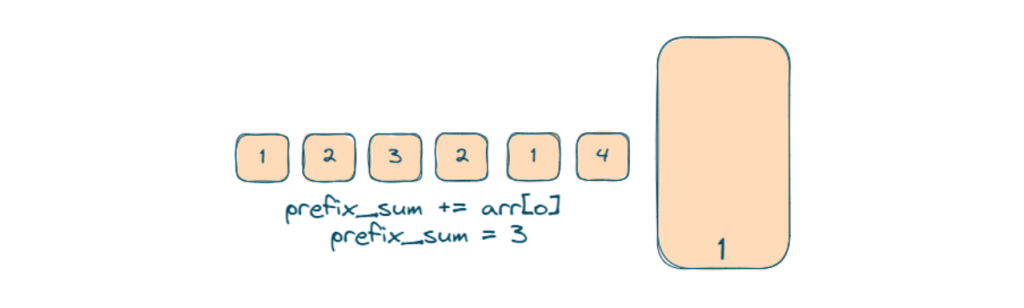
- We will run a loop that iterates through the array, updating prefix_sum and checking if (prefix_sum – k) exists in sum_count.
- The count is updated based on the frequency stored in sum_count
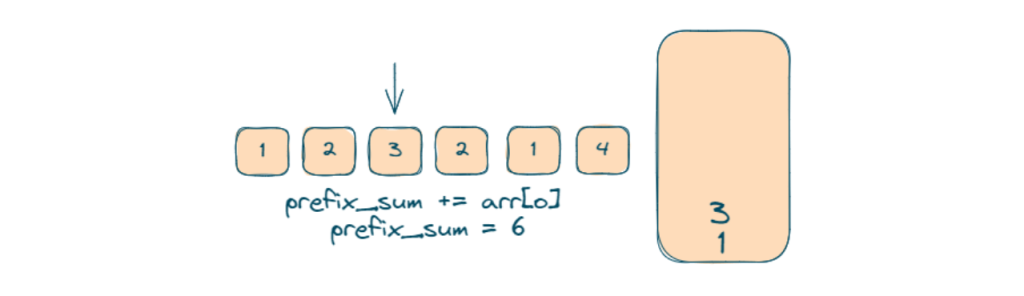
- Now we obtain for index 2 prefix_sum = 6 and (prefix_sum – k) = 1 is already present in hashmap so 2,3 is one of our desired subarray
- We will repeat these steps for all indices and maintain a count that will count all these subarrays.
C++ Code
Below is the C++ solution for ‘Subrray Sum Equals K’ problem:
#include<bits/stdc++.h>
using namespace std;
int subarraySum(vector<int>& array, int k) {
int count = 0;
int prefix_Sum = 0;
unordered_map<int, int> sum_Count;
sum_Count[0] = 1;
for (int num : array) {
prefix_Sum += num;
// Check if (prefix_Sum - k) is in sum_Count
if (sum_Count.find(prefix_Sum - k) != sum_Count.end()) {
count += sum_Count[prefix_Sum - k];
}
// Update sumCount with the current prefixSum
sum_Count[prefix_Sum]++;
}
return count;
}
int main() {
vector<int> array = {1, 2, 3, 2, 1, 4};
int k = 5;
int result = subarraySum(array, k);
cout << "Number of subarrays with sum " << k << " = " << result << endl;
return 0;
}Python Code
You can use the prefix sum approach in Python as well:
def subarray_sum(nums, k):
count = 0
prefix_sum = 0
sum_count = {0: 1}
for num in nums:
prefix_sum += num
# Check if (prefix_sum - k) is in sum_count
if prefix_sum - k in sum_count:
count += sum_count[prefix_sum - k]
# Update sum_count with the current prefix_sum
sum_count[prefix_sum] = sum_count.get(prefix_sum, 0) + 1
return count
if __name__ == "__main__":
array = [1, 2, 3, 2, 1, 4]
k = 5
result = subarray_sum(array, k)
print(f"Number of subarrays with sum {k} = {result}")Java Code
Here is the Java program as well:
import java.util.HashMap;
import java.util.Map;
public class SubarraySum {
public static int subarraySum(int[] nums, int k) {
int count = 0;
int prefixSum = 0;
Map<Integer, Integer> sumCount = new HashMap<>();
sumCount.put(0, 1);
for (int num : nums) {
prefixSum += num;
// Check if (prefixSum - k) is in sumCount
if (sumCount.containsKey(prefixSum - k)) {
count += sumCount.get(prefixSum - k);
}
// Update sumCount with the current prefixSum
sumCount.put(prefixSum, sumCount.getOrDefault(prefixSum, 0) + 1);
}
return count;
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 2, 1, 4};
int k = 5;
int result = subarraySum(array, k);
System.out.println("Number of subarrays with sum " + k + " = " + result);
}
}The time complexity of this code is O(n), where n is the size of the input array. This is because the code iterates through the array once, and for each element, it performs constant-time operations (lookups and updates in the unordered_map).
The space complexity is O(n) for the map data structure that we are using in this approach
Here is a comparative analysis of both the approaches:
| Approaches | Time complexity | Space complexity | Details |
| Brute Force Approach | O(n3) | O(1) | We are using a nested loop for finding the subarray with sum k and inside the nested loop there is another loop to sum all the elements of the subarray. |
| Prefix Sum Approach | O(n) | O(n) | The code iterates through the array once, and for each element, it performs constant-time operations (lookups and updates in the unordered_map). |
Conclusion
In conclusion, the “subarray sum equals k” leetcode problem is used to find the number of subarrays whose sum of elements is equal to the value k. It can be efficiently solved using the prefix sum approach, significantly improving the brute force approach. The prefix sum technique along with a hashmap to efficiently find subarrays with a sum equal to k. With the time complexity of O(n).