Interval-related questions are frequently asked in technical interviews, and they are usually hard to solve. Some of them are Insert Interval, Merge Interval, Meeting Room, etc. This article will explore various approaches to solving the Merge Intervals Problem.
What is the Merge Intervals Problem?
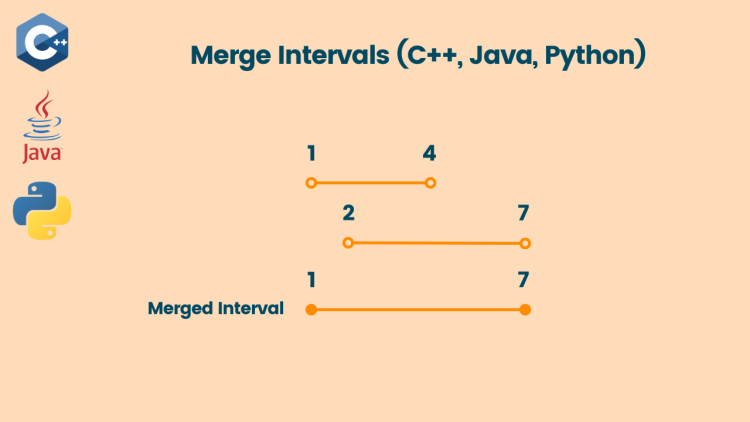
In the Merge Interval problem, you are given an array of intervals that can be arranged in any order. Your task is to return an array of intervals such that no two intervals overlap.
Example:
Input: [[1,4], [2,7], [8,10]]
Output: [[1,7], [8,10]]
Explanation: As 2, 3, 4 lies between 1 to 4 intervals so 1 to 7 become one interval and the other will be 8 to 10.
Brute Force Approach
To solve it the Merge Intervals problem, we will first sort the array based on the starting value of each interval. Once the array is sorted we will compare all the values in the given interval to intervals already present in the resultant array.
Then, Check whether they lie between other intervals or not. If they lie then we will update the interval in the resultant array to a new interval otherwise we will push this interval to the resultant interval.
Let dry run this approach:
- Array given is [[1,4], [7,9], [2,6], [8,10]].
- After sorting the given array, it becomes [[1,4], [2,6], [7,9], [8,10]].
- Create an empty resultant array [].
- Check if the current interval from the given array already lies within the resultant array. If it does, then update the resultant array.
- In the case of [1, 4], the resultant array is empty, so push this interval directly into the resultant array.
- In case [2, 6] as [1, 4] is already there and [2, 6] and [1, 4] overlap so simply update [1, 4] to [1, 6].
- In case [7, 9] as it does not overlap with [1, 6] so push this into the array.
- In case [8, 10] as it overlaps with [7, 9]. Update [7, 9] to [7, 10].
As in this case, we are checking each value of the given array to all the values present in the resultant array so the time complexity will be O(n^2) in the worst case. Space Complexity will be O(n) as we are using an extra array to store our values.
Sorting to Solve Merge Intervals Problem
Before you move forward, you can also go through some sorting algorithms and understand their time complexity. This problem incorporates concepts from sorting.
To solve the Merge Intervals problem, first, we will sort the given array. As the array becomes sorted the interval at a lower index will always have a lower or equal starting time than the intervals at a higher index. Then only two cases are there when they overlap.
One when the latter one will completely lie in between the previous one. Or when the latter has a starting time lower than or equal to the end time of the previous interval.
Let’s do this step-by-step:
- First sort the given array.
- Now create an empty array that will be returning as a resultant. Also, create two variables start and end.
- Initialize start with the starting value and end with the ending value of the first interval.
- Iterate over the array and check if the interval lies between the start and the end values. If they lie between, then update the start with the minimum of the start and the starting value of the current interval, and update the end with the maximum of the end and the ending value of the interval.
- If they do not lie in between then push our start and end to the resultant array.
Time complexity will be O(n log (n) ). As in this case we first sort the array which required n log(n) time and n for iterating over the loop so the total time complexity is n log(n) + n which is around n log(n). Space complexity will remain the same i.e. O(n) for the resultant array.
Space Optimized Approach
In the above approach, we still required O(n) space but this can be reduced to O(1) if we do not use an extra array. It can achieved if we make changes in our actual array only. Here is the optimized approach to merge intervals:
- Sort the given array in ascending order.
- Create a variable with the name temp which points to the current index.
- Iterate over the array and compare if the value at index temp and the value at current index overlap or not. If they overlap then update the interval at index temp as arr[temp][0] = min( arr[temp][0], arr[i][0]), arr[temp][1] = max( arr[temp][1], arr[i][1]). If not then update temp to temp + 1 and then arr[temp] = arr[i].
Let us look at the code for the above solution.
C++ Code
The below C++ program is using space optimized apporach for Merge Interval problem:
#include <bits/stdc++.h>
using namespace std;
int main(){
// inital intervals
vector<vector<int>> intervals = {{1,4},{2,6}, {7,9}, {8,10}};
sort(intervals.begin(), intervals.end());
int temp=0;
int n = intervals.size();
for(int i=1;i<n;i++){
if(intervals[temp][1] >= intervals[i][0]){
intervals[temp][1] = max(intervals[temp][1], intervals[i][1]);
}else {
temp++;
intervals[temp][0]= intervals[i][0];
intervals[temp][1]= intervals[i][1];
}
}
for(int i=0;i<=temp;i++){
cout<<intervals[i][0]<<" "<<intervals[i][1]<<endl;
}
return 0;
}Java Code
You can do it with Java too:
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[][] intervals = {{1,4},{2,6}, {7,9}, {8,10}};
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
int temp = 0;
int n = intervals.length;
for (int i = 1; i < n; i++) {
if (intervals[temp][1] >= intervals[i][0]) {
intervals[temp][1] = Math.max(intervals[temp][1], intervals[i][1]);
} else {
temp++;
intervals[temp][0] = intervals[i][0];
intervals[temp][1] = intervals[i][1];
}
}
for (int i = 0; i <= temp; i++) {
System.out.println(intervals[i][0] + " " + intervals[i][1]);
}
}
}Python Code
Here is the Python program to solve it:
intervals = [[1,4],[2,6], [7,9], [8,10]]
intervals.sort()
temp = 0
n = len(intervals)
for i in range(1, n):
if intervals[temp][1] >= intervals[i][0]:
intervals[temp][1] = max(intervals[temp][1], intervals[i][1])
else:
temp += 1
intervals[temp][0] = intervals[i][0]
intervals[temp][1] = intervals[i][1]
for i in range(temp + 1):
print(intervals[i][0], intervals[i][1])Output:
1 6
7 10In the above approach, we can see that we are not using any extra space so space complexity will reduced to O(1). Time complexity will remain the same as above i.e. O(n log(n)) because we are doing sorting here.
You can compare all the 3 approaches to find out which works for you:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O( n^2) | O(n) | We are using two loops to find the overlapping intervals. |
| Optimized Approach | O(n Log(n) ) | O(n) | We are using a sorting function that requires O( n Log(n) ) time complexity. |
| Space Optimized | O(n Log(n) ) | O(1) | We are not using any extra space. |
Conclusion
We have seen various approaches to solve the Merge Interval problem from leetcode. The best is the space-optimized approach because it minimizes both time and space complexity.