In programming interviews, there are many leetcode problems related to arrays and one of them is the majority element. In this article, we will explore different approaches to find the optimal solution for this problem and discuss their time complexities.
What is the Majority Element?
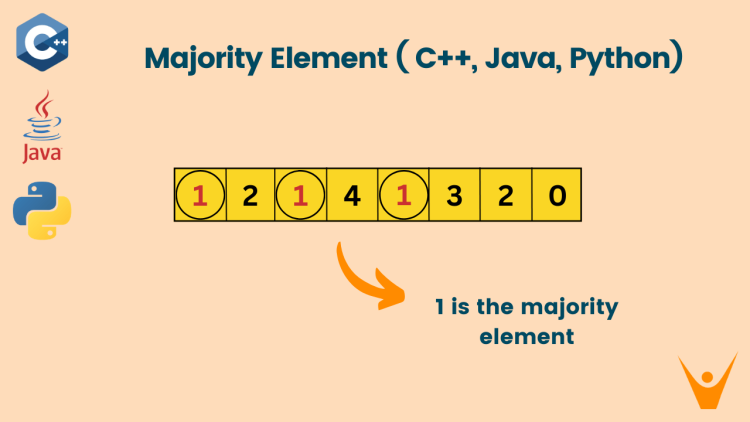
In this problem, we are given an array and our main goal is to find the majority element in an array. The majority element is defined as an element that occurs more than N/2 times in the given array, where N represents the size of the array.
Let us understand it better with an example:
Array = [3, 3, 4, 2, 4, 4, 2, 4, 4]
Output = 4
Output is 4 as 4 appears 5 times and the total length of the array is 9:

Brute Force Approach: Using Hashmap
In this approach, we will use hashmap to count the number of occurrences of each element and check which element is occurring more than n/2 times where n is the size of our array.
Here are the steps to solve this problem:
- Firstly we will declare a hashmap to store the count of each element and then we will run a loop to store the element with their occurrence in the hashmap.

- Now we will run a loop to search for the majority element in the map and if there is no such element in the map then we will return -1.
The time complexity for this approach is O(n*logn) + O(n) where n is the size of the array as the map data structure takes logN time for insertion as we are doing it for n elements in the array and O(n) for searching it.
The space complexity of this approach is O(m) as we are using map data structure and m is the number of unique elements present in the map
Optimal Approach: Moore’s Voting Algorithm
The Boyer-Moore Majority Vote Algorithm is an optimal algorithm for finding the majority element in a sequence of elements. The algorithm was proposed by Robert S. Boyer and J Strother Moore in 1980 and is particularly efficient for our purpose.
Here are the steps to implement this algorithm:
- Firstly we will declare a count variable to keep track of the count and an element variable to store the potential majority element.
- We will start iterating through the array and if the count is 0 set the value of the element equal to the current element and increment count.
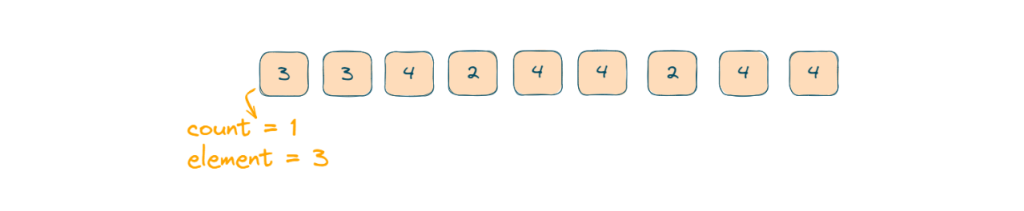
- If the current element is equal to the element, increment count; otherwise, decrement count. And if the count goes less than 0 set it to 0

- Here 4 is not equal to 3 so we will decrease the count and as the count is not 0 our element will remain the same.
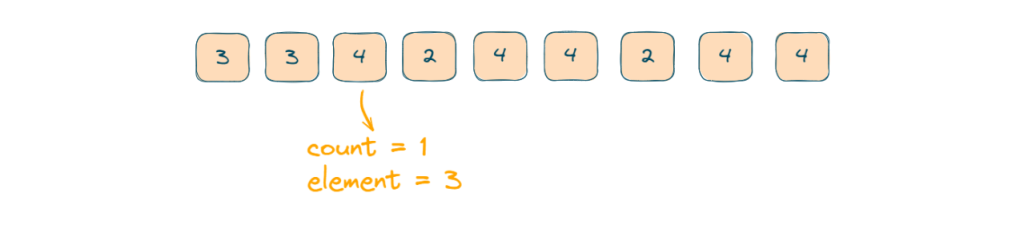
- Now when our pointer comes on 2 again count will decrement and becomes 0.
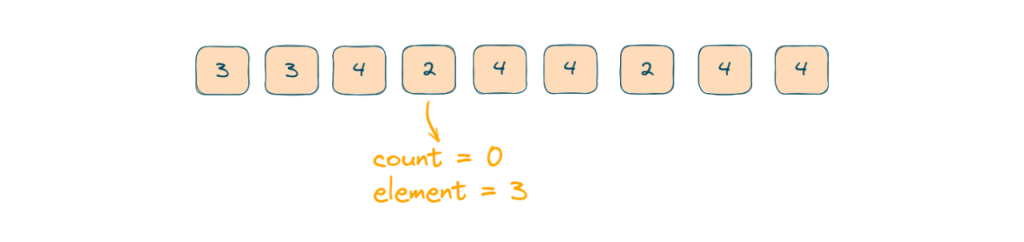
- The count is 0 and the current element is not equal to the element so our element will update and the count will increment.
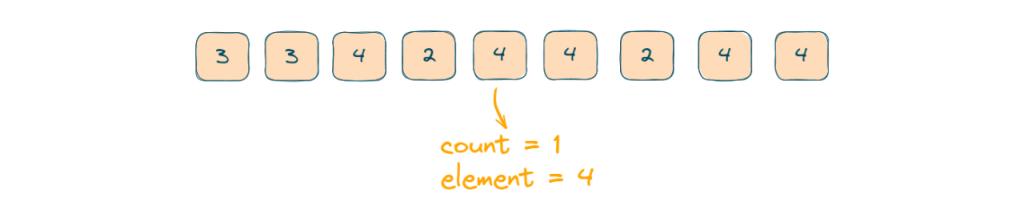
- The current element is equal to the element so the count will increment and the element will remain the same.
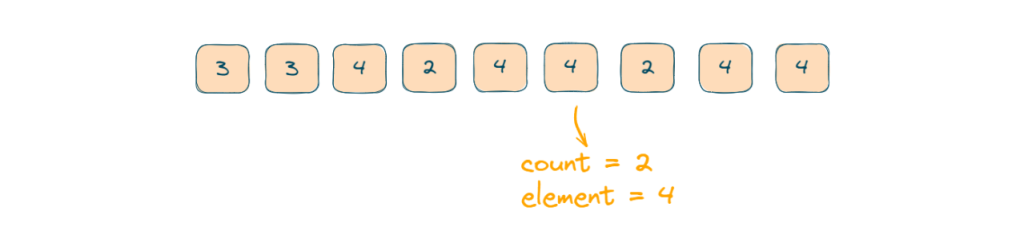
- The count will decrease as the current element is not the same as the element but the element will not change as the count is not 0.

- For the next two steps count will increment as the current element is equal to the element.


- After the iteration element is the potential element to verify it we will run a loop to check whether the potential element is the actual majority element or not.
C++ Code
Here is the C++ program to find the majority element in an array:
#include<bits/stdc++.h>
using namespace std;
int majorityElement(vector<int>& nums) {
// Initialize variables to track the current candidate element and its count
int element = 0;
int count = 0;
// Traverse the array
for (int i = 0; i < nums.size(); i++) {
// If the count is 0, update the current element
if (count == 0) {
element = nums[i];
}
// Update count based on whether the current element is equal to the candidate element
if (nums[i] == element) {
count++;
} else {
count--;
}
}
// Check if the candidate element is the majority element
int countCheck = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] == element) {
countCheck++;
}
}
// If the count of the candidate element is greater than half the array size, it is the majority element
if (countCheck > nums.size() / 2) {
return element;
}
// If there is no major element, return -1
return -1;
}
int main() {
// Example array
vector<int> nums = {3, 3, 4, 2, 4, 4, 2, 4, 4};
// Find the majority element using the function
int result = majorityElement(nums);
// Print the result
if (result != -1) {
cout << "The majority element is: " << result << endl;
}
else {
cout << "There is no majority element." << endl;
}
// Return 0 to indicate successful completion
return 0;
}Java Code
Below is the Java code to solve this problem:
import java.util.HashMap;
import java.util.Map;
public class MajorityElement {
public static int majorityElement(int[] nums) {
// Initialize variables to track the current candidate element and its count
int element = 0;
int count = 0;
// Traverse the array
for (int num : nums) {
// If the count is 0, update the current element
if (count == 0) {
element = num;
}
// Update count based on whether the current element is equal to the candidate element
if (num == element) {
count++;
}
else {
count--;
}
}
// Check if the candidate element is the majority element
int countCheck = 0;
for (int num : nums) {
if (num == element) {
countCheck++;
}
}
// If the count of the candidate element is greater than half the array size, it is the majority element
if (countCheck > nums.length / 2) {
return element;
}
// If there is no major element, return -1
return -1;
}
public static void main(String[] args) {
// Example array
int[] nums = {3, 3, 4, 2, 4, 4, 2, 4, 4};
// Find the majority element using the function
int result = majorityElement(nums);
// Print the result
if (result != -1) {
System.out.println("The majority element is: " + result);
}
else {
System.out.println("There is no majority element.");
}
}
}Python Code
You can implement the algorithm in Python too:
def majority_element(nums):
# Initialize variables to track the current candidate element and its count
element = 0
count = 0
# Traverse the array
for num in nums:
# If the count is 0, update the current element
if count == 0:
element = num
# Update count based on whether the current element is equal to the candidate element
if num == element:
count += 1
else:
count -= 1
# Check if the candidate element is the majority element
count_check = 0
for num in nums:
if num == element:
count_check += 1
# If the count of the candidate element is greater than half the array size, it is the majority element
if count_check > len(nums) // 2:
return element
# If there is no major element, return -1
return -1
# Example array
nums = [3, 3, 4, 2, 4, 4, 2, 4, 4]
# Find the majority element using the function
result = majority_element(nums)
# Print the result
if result != -1:
print("The majority element is:", result)
else:
print("There is no majority element.")Output:
The majority element is: 4The time complexity for this approach is O(n) + O(n): O(n) for finding the potential majority element and another O(n) for checking whether it is the actual majority element or not.
The space complexity for this approach is O(1) as we are not using any extra space.
Below is a comparison of both methods:
| Approach | Time complexity | Space complexity | Detail |
| Hashmap approach | O(n*logn) + O(n) | O(m) | It takes logN time for insertion and we are doing it for n element in the array and O(n) for searching it. |
| Moore voting algorithm | O(n) + O(n) | O(1) | O(n) for finding the potential element and another O(n) for checking whether the it is the actual majority element or not. |
Conclusion
In conclusion, the majority element leetcode problem involves finding an element that occurs more than n/2 times in an array. In this article, we have discussed two approaches with their time complexities and came to know that the Moore voting algorithm helps us to solve this problem in linear time complexity.