In the domain of computer science and data management, efficient caching mechanisms play an important role in enhancing system performance. One of the cache replacement policies is the least recently used algorithm. In this article, we will discuss the fundamentals of the LRU cache problem from leetcode, exploring its concept, and the queue hashing approach with solution.
What is LRU Cache Implementation?
LRU, or Least Recently Used, is a caching strategy where the system keeps track of the usage history of cached elements and discards the least recently used item when the cache reaches its capacity. This strategy ensures that the most recently used items are retained, optimizing cache utilization and improving overall performance.
Let’s discuss how we can implement LRU Cache!
Using Queue and Hashing Approach
The Queue Hashing Approach is a common method for implementing LRU cache. It combines the efficiency of a queue for tracking usage history and a hashmap for quick lookups. The queue maintains the order of element access, and the hash map facilitates fast retrieval of elements.
The Data Structures used in this approach:
- Queue: We will maintain a queue to represent the order of access. When an element is accessed or inserted, it is moved to the front of the queue.
- Hash Map: Utilize a hashmap to store the elements along with their corresponding positions in the queue.
The functions to be implemented in this problem:
- Firstly we will declare a member variable in a private class
- capacity: This indicates the maximum number of elements the cache can hold.
- cacheMap: An unordered map that stores the key-value pairs along with iterators pointing to their positions in the cacheList.
- cacheList: A doubly-linked list that maintains the order of element access.
- LRUCache(int capacity): Initialize the LRU cache with positive size capacity.
- int get(int key): Return the value of the key if the key exists, otherwise, return -1.
- The get function checks if the key is present in the cache. If it’s not found, it returns -1. If the key is found, it moves the corresponding element to the front of the cache list using the splice function and returns the value associated with the key.
- void put(int key, int value): Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.
- The put function handles inserting a new element or updating an existing one. If the key is already present, it updates the value and moves the element to the front of the cache list.
- If the key is not present, it inserts the new element at the front. If the cache is at full capacity, it removes the least recently used element from both the cacheList and cacheMap.
Let’s consider an example:
Input = [“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
Output = [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Here is an explanation for the example:
- In this firstly we are declaring LRU of size 2
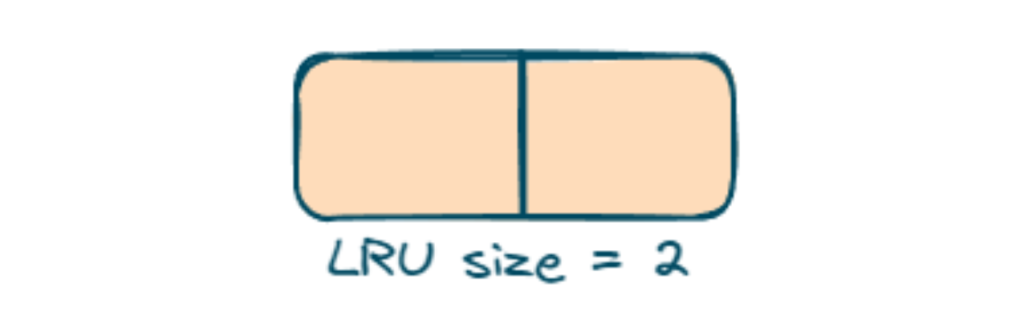
- lRUCache.put(1, 1); we will put value one with key 1
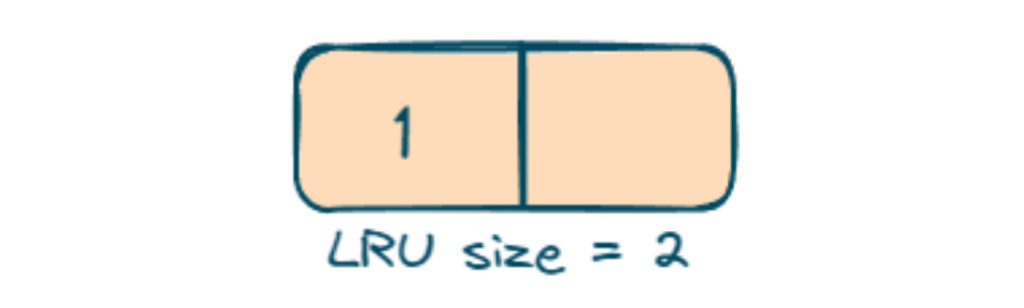
- lRUCache.put(2, 2); we will put value 2 with key 2
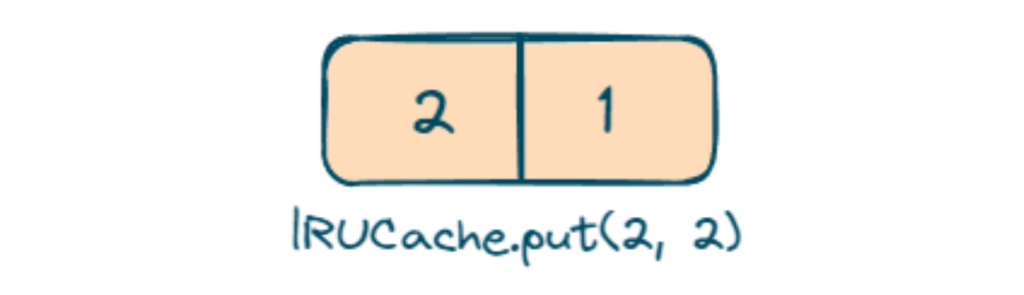
- Now if we do LRUCache.get(1) we will get 1 because 1 is present in the queue
- lRUCache.put(3, 3); we will put the value 3 with key 3 now key 2 is evicted because 1 was recently used.
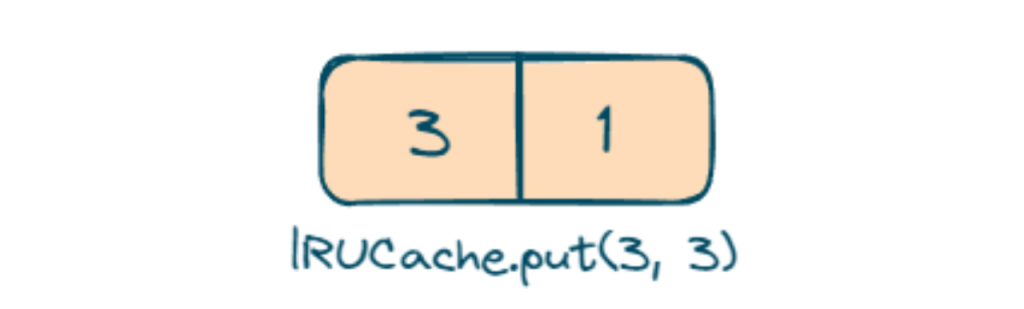
- lRUCache.put(4, 4); we will put value 4 with key 4
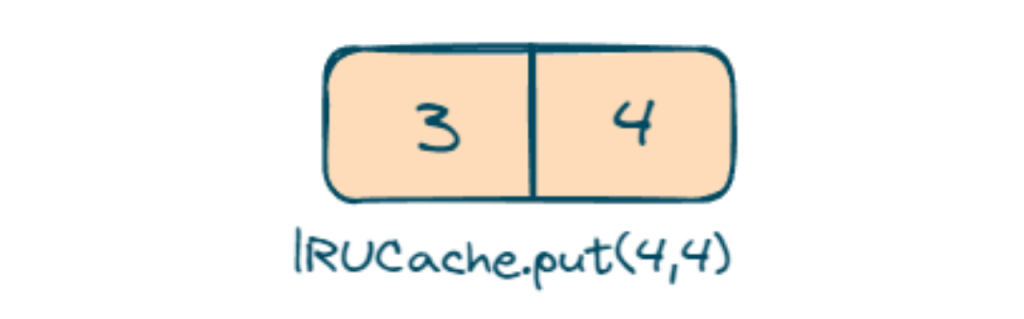
- lRUCache.get(1); return -1 because 1 is not present.
- Now if we do LRUCache.get(3) we will get 3 because 3 is present in the queue
- LRUCache.get(4) we will get 4 because 4 is present in the queue
C++ Code
Here is the C++ program to implement LRU cache using Queue and Hashing:
#include <iostream>
#include <unordered_map>
#include <list>
using namespace std;
class LRUCache {
private:
int capacity;
unordered_map<int, list<pair<int, int>>::iterator> cacheMap;
list<pair<int, int>> cacheList;
public:
LRUCache(int capacity) : capacity(capacity) {}
int get(int key) {
if (cacheMap.find(key) == cacheMap.end()) {
return -1;
}
// Move the accessed element to the front of the list
cacheList.splice(cacheList.begin(), cacheList, cacheMap[key]);
return cacheMap[key]->second;
}
void put(int key, int value) {
if (cacheMap.find(key) != cacheMap.end()) {
// Update the value and move the element to the front
cacheMap[key]->second = value;
cacheList.splice(cacheList.begin(), cacheList, cacheMap[key]);
} else {
// Insert the new element
if (cacheList.size() == capacity) {
int lastKey = cacheList.back().first;
cacheMap.erase(lastKey);
cacheList.pop_back();
}
cacheList.emplace_front(key, value);
cacheMap[key] = cacheList.begin();
}
}
};
int main() {
// Example Usage
LRUCache lruCache(2);
lruCache.put(1, 1);
lruCache.put(2, 2);
cout << lruCache.get(1) << endl; // Output: 1
lruCache.put(3, 3);
cout << lruCache.get(2) << endl; // Output: -1 (not found)
lruCache.put(4, 4);
cout << lruCache.get(1) << endl; // Output: -1 (not found)
cout << lruCache.get(3) << endl; // Output: 3
cout << lruCache.get(4) << endl; // Output: 4
return 0;
}Java Code
Here is the Java program to implement LRU cache:
import java.util.LinkedHashMap;
import java.util.Map;
class LRUCache {
private final int capacity;
private final LinkedHashMap<Integer, Integer> cache;
public LRUCache(int capacity) {
this.capacity = capacity;
this.cache = new LinkedHashMap<>(capacity, 0.75f, true) {
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
};
}
public int get(int key) {
return cache.getOrDefault(key, -1);
}
public void put(int key, int value) {
cache.put(key, value);
}
public static void main(String[] args) {
// Example Usage
LRUCache lruCache = new LRUCache(2);
lruCache.put(1, 1);
lruCache.put(2, 2);
System.out.println(lruCache.get(1)); // Output: 1
lruCache.put(3, 3);
System.out.println(lruCache.get(2)); // Output: -1 (not found)
lruCache.put(4, 4);
System.out.println(lruCache.get(1)); // Output: -1 (not found)
System.out.println(lruCache.get(3)); // Output: 3
System.out.println(lruCache.get(4)); // Output: 4
}
}Python Code
You can implement it in Python as well:
from collections import OrderedDict
class LRUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.cache = OrderedDict()
def get(self, key: int) -> int:
return self.cache.get(key, -1)
def put(self, key: int, value: int) -> None:
if key in self.cache:
del self.cache[key]
elif len(self.cache) >= self.capacity:
self.cache.popitem(last=False)
self.cache[key] = value
# Example Usage
lru_cache = LRUCache(2)
lru_cache.put(1, 1)
lru_cache.put(2, 2)
print(lru_cache.get(1)) # Output: 1
lru_cache.put(3, 3)
print(lru_cache.get(2)) # Output: -1 (not found)
lru_cache.put(4, 4)
print(lru_cache.get(1)) # Output: -1 (not found)
print(lru_cache.get(3)) # Output: 3
print(lru_cache.get(4)) # Output: 4Output:
1
-1
-1
3
4
Complexity Analysis
Let’s try to understand the time and space complexity of the same.
Time Complexity:
get(key):
- Searching for the key in the unordered_map takes O(1) time.
- Moving the accessed element to the front of the list using splice also takes O(1) time. Therefore, the overall time complexity of get is O(1).
put(key, value):
- If the key already exists, updating the value and moving the element to the front both take O(1) time.
- If the key is not present: Inserting a new element into the list takes O(1) time.
- If the cache is at full capacity, removing the least recently used element from both the list and the map takes O(1) time.
Therefore, the overall time complexity of put is O(1).
Space Complexity:
- The space complexity is determined by the capacity of the cache.
- The unordered_map (cacheMap) stores at most ‘capacity’ entries, each taking O(1) space.
- The doubly-linked list (cacheList) also stores at most ‘capacity’ entries, each taking O(1) space.
Therefore, the overall space complexity is O(capacity).
Conclusion
In conclusion, understanding and implementing LRU cache is crucial for optimizing data retrieval in systems with limited resources, and the Queue Hashing Approach provides an efficient solution to this need. The provided code examples demonstrate the versatility of LRU cache implementation across different programming languages. Learn about Hashing in Data Structures to know how it works as well.








