The Longest Increasing Subsequence (LIS) problem is a classic problem in computer science. In this article, we will explore different approaches to solving this problem and discuss their time and space complexities.
What is the Longest Increasing Subsequence?
The longest subsequence problem involves finding the longest subsequence in the array that is in increasing order.
Let us try to understand the problem using an example.
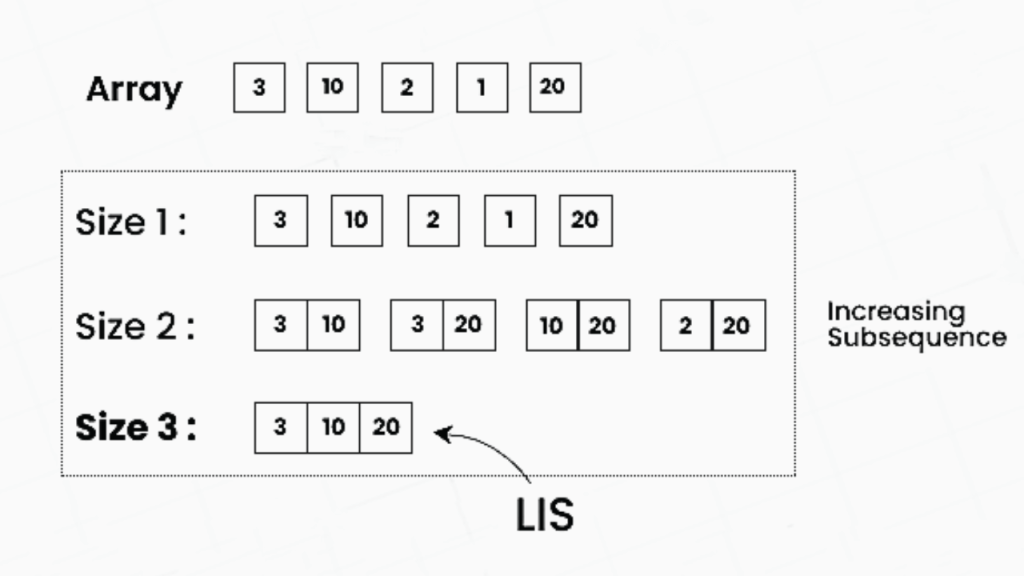
- Consider the following array {9, 20, 8, 5, 30}
- Please note that a consecutive subsequence of an array is a subarray formed by elements of the array, by erasing the elements to the right if required.
- Hence, to find the increasing subsequence, we can remove the element next, if it is not greater.
- Hence, we can make 1-size, 2-size, and 3-size subsequences as shown below.
Let’s now discuss the various approaches with different time complexities.
Naive Approach
The naive recursive approach to finding the Longest Increasing Subsequence (LIS) involves exploring all possible subsequences of the input array to identify the longest increasing subsequence. This approach provides a clear illustration of the problem.
The naive recursive approach exhaustively explores all possibilities, which can be quite slow for large input arrays.
This approach is less efficient in terms of time complexity and may not be suitable for solving large instances of the problem, but it provides a clear understanding of the problem’s nature and can serve as a foundation for developing more optimized solutions.
The time complexity of the naive recursive approach is exponential, specifically O(2^n), where ‘n’ is the number of elements in the input array. This is because the algorithm explores all possible subsequences, resulting in a branching factor of 2 for each element in the array.
Dynamic Programming Approach
The dynamic programming approach to solve the Longest Increasing Subsequence problem involves using a table to store the length of the LIS ending at each index in the array.
Here’s how the dynamic programming approach works:
- Initialize an array to keep track of the length of the LIS ending at each index in the input array.
- Iterate through the elements in the input array, one by one.
- For each element, compare it with all the previous elements in the array.
- If the current element is greater than a previous element, update the LIS length for the current element, considering the possibility of extending the LIS.
- Continuously keep track of the maximum LIS length as you go through the array.
- The final answer to the problem is the maximum length found during this process.
C++ Code
Here is the C++ program to find the longest increasing subsequence using dynamic programming:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Function to find the length of the Longest Increasing Subsequence (LIS)
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
/**
*Create a DP (Dynamic Programming) array to
*store the length of LIS ending at each index
*/
vector<int> dp(n, 1);
// Iterate through the elements of the input array
for (int i = 0; i < n; i++) {
// Compare the current element with all previous elements
for (int j = 0; j < i; j++) {
/**
* If the current element is greater than the previous element,
* update the LIS length at the current index
*/
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
// Find the maximum value in the DP array
return *max_element(dp.begin(), dp.end());
}
int main() {
vector<int> nums = {10, 9, 2, 5, 3, 7, 101, 18};
int result = lengthOfLIS(nums);
cout << "Length of the Longest Increasing Subsequence: " << result << endl;
return 0;
}Python Code
Here is the complete python program:
def lengthOfLIS(nums):
n = len(nums)
# Create a DP (Dynamic Programming) array to store the length of LIS ending at each index
dp = [1] * n
# Iterate through the elements of the input array
for i in range(n):
# Compare the current element with all previous elements
for j in range(i):
# If the current element is greater than the previous element,
# update the LIS length at the current index
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
# Find the maximum value in the DP array, which represents the longest LIS
return max(dp)
nums = [10, 9, 2, 5, 3, 7, 101, 18]
result = lengthOfLIS(nums)
print("Length of the Longest Increasing Subsequence:", result)Java Code
Here is the Java program to look for the longest increasing subsequence:
import java.util.Arrays;
public class LongestIncreasingSubsequence {
public static int lengthOfLIS(int[] nums) {
int n = nums.length;
/**
* Create a DP (Dynamic Programming) array to
* store the length of LIS ending at each index
*/
int[] dp = new int[n];
Arrays.fill(dp, 1);
// Iterate through the elements of the input array
for (int i = 0; i < n; i++) {
// Compare the current element with all previous elements
for (int j = 0; j < i; j++) {
/**
* If the current element is greater than the previous element,
* update the LIS length at the current index
*/
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
// Find the maximum value in the DP array
int max = 0;
for (int len : dp) {
max = Math.max(max, len);
}
return max;
}
public static void main(String[] args) {
int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};
int result = lengthOfLIS(nums);
System.out.println("Length of the Longest Increasing Subsequence: " + result);
}
}Output:
Length of the Longest Increasing Subsequence: 4The time complexity of the dynamic programming approach for solving the Longest Increasing Subsequence (LIS) problem is O(n^2), where ‘n’ represents the number of elements in the input array. This is mainly due to the nested loops where we compare elements and update the DP array.
In the worst case, the algorithm iterates through all elements in the outer loop and checks against all previous elements in the inner loop, resulting in a quadratic time complexity.
Greedy Approach with Binary Search
The greedy approach with binary search is an optimized version of the dynamic programming approach. The efficient approach uses a combination of greedy strategy and binary search to find the longest increasing subsequence.
In this approach, we maintain an array tail where tail[i] represents the smallest possible ending element of all increasing subsequences of length i+1. We iterate through the input array and update the tail array accordingly.
The length of the longest increasing subsequence is equal to the length of the tail array. We can use binary search to find the correct position to update the tail array, ensuring that the array remains sorted in ascending order.
Let us try to understand the approach using an example.
Consider the following array {1, 5, 2, 4, 3}
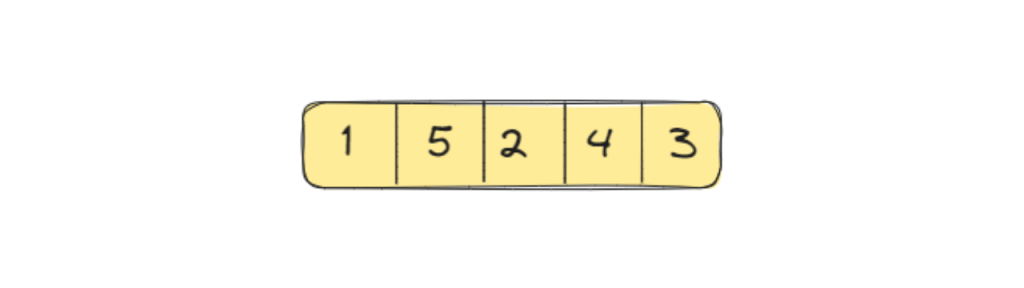
Now, we will be maintaining an array of tails and updating it accordingly.
We will start by keeping a pointer at the 0th index and then update it accordingly.
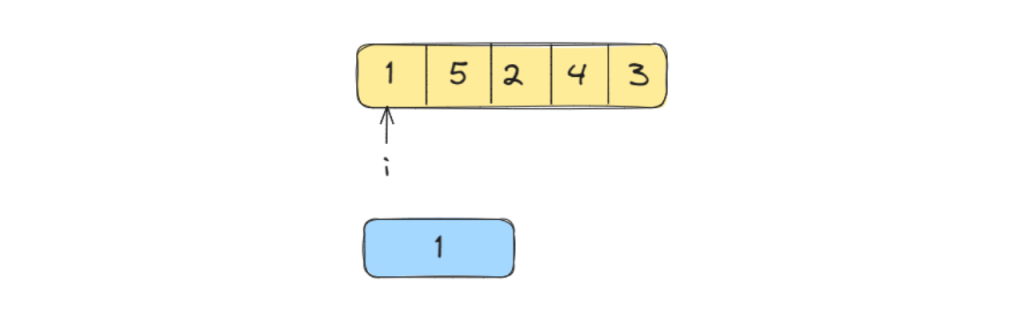
Since the array is empty, we can add 1 directly into it as there is no number that can be greater than it in the array.
Similarly, we will move forward and check whether the next number is greater than the current number in the array.
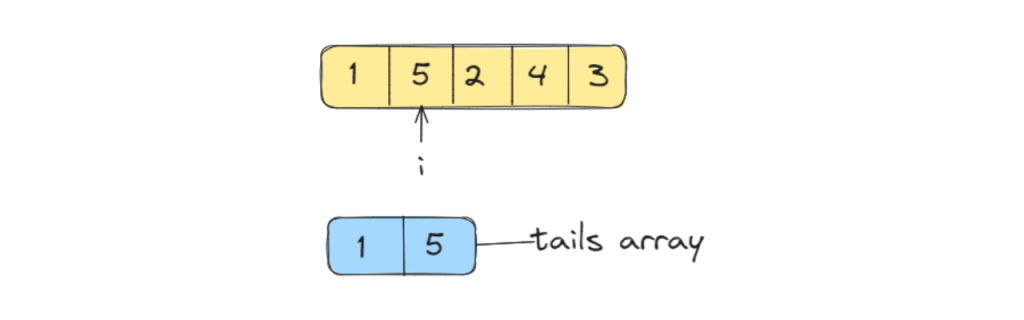
Again since 5 is greater than 1, it will be directly added to the array.
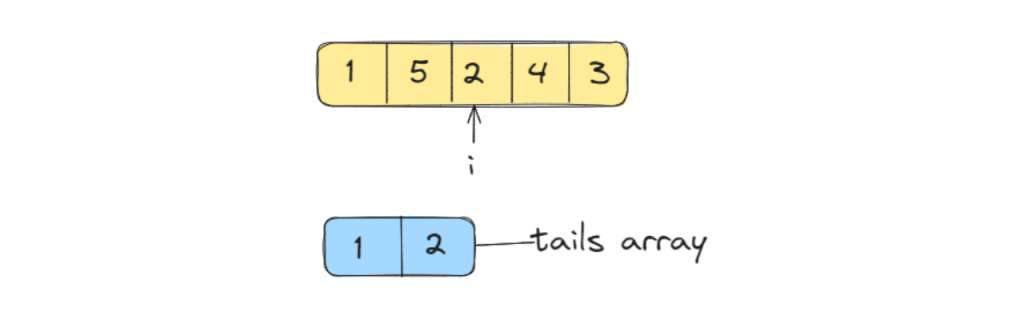
Now, we can see that 2 is not greater than 5, hence it cannot be included in the current sequence. But it is greater than 1 and can start a new subsequence which can eventually turn out to be greater than the current subsequence. Hence, we will replace it with the position of 5.
Similarly, we will proceed further.
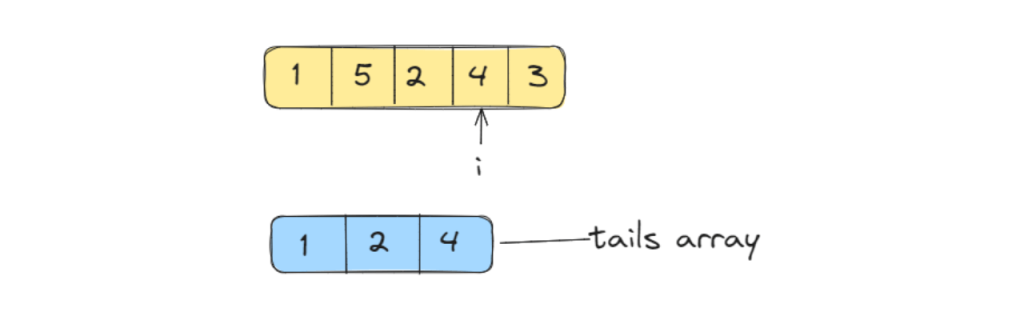
Again, since 4 is greater than 2, it will directly be added to the array.
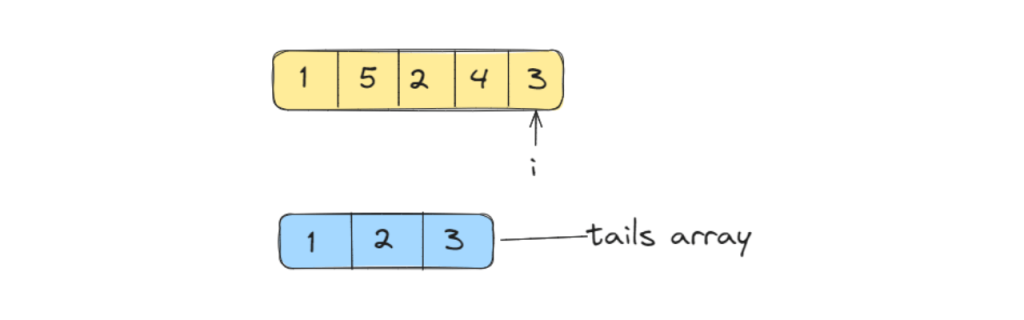
Finally, we can see that 3 is lesser than 4 but greater than 2. Therefore, it will replace 4 in the array.
We can thus realize that the length of our final array is 3.
Hence, the longest increasing subsequence of the array is 3.
C++ Code
Here is the C++ program to solve LIS using Greedy Approach:
#include <bits/stdc++.h>
using namespace std;
/**
* Function to find the length of the Longest Increasing Subsequence (LIS).
*
* @param nums: The input array of integers.
* @return The length of the Longest Increasing Subsequence.
*/
int lengthOfLIS(vector<int>& nums) {
// Create an empty vector 'tail' to store the elements of the LIS.
vector<int> tail;
// Iterate through the input 'nums'.
for (int num : nums) {
// Use binary search to find the position where 'num' should be inserted.
auto it = lower_bound(tail.begin(), tail.end(), num);
// If 'it' points to the end of 'tail', 'num' is greater than all elements.
if (it == tail.end()) {
// Add 'num' to the end of 'tail'.
tail.push_back(num);
} else {
// Replace the element at 'it' with 'num' to maintain an increasing subsequence.
*it = num;
}
}
// Return the size of 'tail', which represents the length of the LIS.
return tail.size();
}
int main() {
vector<int> nums = {10, 9, 2, 5, 3, 7, 101, 18};
int result = lengthOfLIS(nums);
cout << "Length of the Longest Increasing Subsequence: " << result << endl;
return 0;
}Python Code
Below is the Python program:
def lengthOfLIS(nums):
# Create an empty list 'tail' to store the elements of the LIS.
tail = []
# Iterate through the input 'nums'.
for num in nums:
# Use binary search to find the position where 'num' should be inserted.
it = bisect_left(tail, num)
# If 'it' points to the end of 'tail', 'num' is greater than all elements.
if it == len(tail):
# Add 'num' to the end of 'tail'.
tail.append(num)
else:
# Replace the element at 'it' with 'num' to maintain an increasing subsequence.
tail[it] = num
# Return the length of 'tail', which represents the length of the LIS.
return len(tail)
nums = [10, 9, 2, 5, 3, 7, 101, 18]
result = lengthOfLIS(nums)
print("Length of the Longest Increasing Subsequence:", result)Java Code
Below is the Java program for Longest Increasing Subsequence using Greedy Approach:
import java.util.Arrays;
public class LongestIncreasingSubsequence {
/**
* Function to find the length of the Longest Increasing Subsequence (LIS).
*
* @param nums: The input array of integers.
* @return The length of the Longest Increasing Subsequence.
*/
public static int lengthOfLIS(int[] nums) {
// Create an empty array 'tail' to store the elements of the LIS.
int[] tail = new int[nums.length];
int len = 0;
// Iterate through the input 'nums'.
for (int num : nums) {
// Use binary search to find the position where 'num' should be inserted.
int it = Arrays.binarySearch(tail, 0, len, num);
// If 'it' is negative, calculate the index where 'num' should be inserted.
it = -(it + 1);
// If 'it' is equal to 'len', 'num' is greater than all elements.
if (it == len) {
// Add 'num' to 'tail'.
tail[len] = num;
len++;
}
else {
// Replace the element at 'it' with 'num' to maintain an increasing subsequence.
tail[it] = num;
}
}
// 'len' represents the length of the LIS.
return len;
}
public static void main(String[] args) {
int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};
int result = lengthOfLIS(nums);
System.out.println("Length of the Longest Increasing Subsequence: " + result);
}
}Output:
Length of the Longest Increasing Subsequence: 4The time complexity of this algorithm is O(nlog(n)), where ‘n’ is the number of elements in the input ‘nums’. The dominant factor in the time complexity is the lower_bound function, which performs binary search on the ‘tail’ vector. For each element in ‘nums’, the lower_bound operation takes logarithmic time. Therefore, in the worst case, the entire loop takes O(nlog(n)) time.
The greedy approach is more efficient than a standard dynamic programming solution for finding the Longest Increasing Subsequence, which has a time complexity of O(n^2).
Let’s see a quick review of all three approaches.
| Approach | Time Complexity | Space Complexity | Details |
| Naive/ Recursive | O(2^n) | O(1) | The naive recursive approach explores all possible subsequences, making it less efficient for large input arrays |
| Dynamic Programming | O(n^2) | O(n) | The dynamic programming approach uses a table to store the length of the LIS ending at each index in the array. |
| Binary Search | O(n*log(n)) | O(n) | It uses a combination of greedy strategy and binary search to efficiently find the LIS |
Conclusion
In this article, we explored different approaches to solving the Longest Increasing Subsequence problem. We discussed the naive recursive approach, the dynamic programming approach, and the optimized greedy approach with binary search. Each approach has its advantages and trade-offs, and understanding them is crucial when choosing the right approach for a specific problem.








