K closest point is a classic coding problem that tells the nearest k points from the origin in a 2-D plane we are given n coordinates of a 2-D plane and we have to tell k points which are closest to the origin. In this article, we will see how to find k closest points to the origin using a heap.
What is the K Closest Point to the Origin Problem?
In the K Closest Point to the Origin problem, we are given n number of coordinates of a 2-D plane and we have to tell the k nearest coordinates that are closest to the origin (0,0). The closest points are those whose Euclidean distance from the origin is minimal.
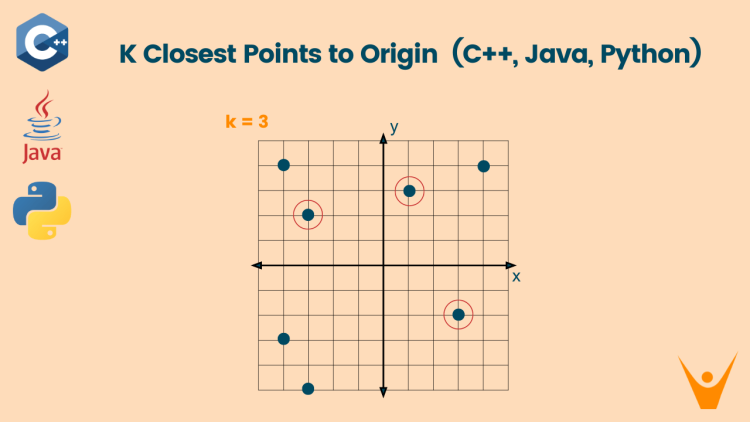
Let us understand it with an example, look at the following figure:
Here is the solution:
Points = [[2,3], [3,5], [-2,2]]
K = 2
Output = [-2, 2] [2, 3]
One way to solve this problem is to find the distance of all the points from the origin and store it in a data structure, let’s say, vector. We will then sort the vector to get the closest distance first. We will iterate the vector till we get k closest points. We will also store the index of the original point along with the distance so that we can reach back to the point.
The time complexity of the brute force technique is O(N log N), where N is the number of points, as we have to sort the vector which will be of size n. The space complexity is O(N) for storing the elements in the vector.
Max-Heap to Find K Closest Points to the Origin
In the max-heap approach to find K closest points to the origin, we will find the Euclidean distance of each point from the origin and store it in max-heap and maintain the size of the priority queue equal to k to store only k closest distance as size increases from k we will pop the highest distance present in the priority queue. By doing this, we will be reducing the space required from O(N) to O(k).
Euclidean distance = √(x-0)2 +(y-0)2 Can be written as √(x)2 +(y)2 Because we are finding distance from origin

Here are the steps to solve this problem using max-heap:
- Firstly we will declare a priority queue (max-heap) where each element is a pair of distance and point.
- Now we will simply run a for loop on points array calculate Euclidean distance from each point and store it in our priority queue
- We will maintain the size of the priority queue as k so whenever the size is more than k we will run a condition and pop the highest element present in the priority queue
- At last, we are left with k elements in the priority queue which are our k closest points.
Now, let’s move to the implementation!
C++ Code
Below is the C++ program to find K closest points to the origin:
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
vector<vector<int>> ans;
// Create a max heap (priority queue) where each element is a pair of distance and point
priority_queue<pair<int, vector<int>>> maxHeap;
// Push points onto the heap, maintaining the size at most k
for (const auto& point : points) {
int distance = point[0] * point[0] + point[1] * point[1];
maxHeap.push({distance, point});
if (maxHeap.size() > k) {
maxHeap.pop(); // Keep the size of the heap at most k
}
}
// Pop elements from the heap and store them in the result
while (!maxHeap.empty()) {
ans.push_back(maxHeap.top().second);
maxHeap.pop();
}
// Reverse the result to get the closest points first
reverse(ans.begin(), ans.end());
return ans;
}
int main() {
// Example usage:
vector<vector<int>> points = {{2, 3}, {3, 5}, {-2, 2}};
int k = 2;
// Find the k closest points
vector<vector<int>> result = kClosest(points, k);
// Print the result
cout << "The " << k << " closest points are:\n";
for (const auto& point : result) {
cout << "[" << point[0] << ", " << point[1] << "] ";
}
return 0;
}Python Code
Here is the Python program for this problem:
import heapq
def k_closest(points, k):
ans = []
# Create a max heap (priority queue) where each element is a pair of distance and point
max_heap = []
# Push points onto the heap, maintaining the size at most k
for point in points:
distance = point[0] ** 2 + point[1] ** 2
heapq.heappush(max_heap, (-distance, point))
if len(max_heap) > k:
heapq.heappop(max_heap) # Keep the size of the heap at most k
# Pop elements from the heap and store them in the result
while max_heap:
distance, point = heapq.heappop(max_heap)
ans.append(point)
# Reverse the result to get the closest points first
ans.reverse()
return ans
# Example usage:
points = [[2, 3], [3, 5], [-2, 2]]
k = 2
# Find the k closest points
result = k_closest(points, k)
# Print the result
print("The", k, "closest points are:")
for point in result:
print(point)Java Code
We have also Java in our arsenal:
import java.util.*;
public class KClosestPoints {
public static List<List<Integer>> kClosest(int[][] points, int k) {
List<List<Integer>> ans = new ArrayList<>();
// Create a max heap (priority queue) where each element is a pair of distance and point
PriorityQueue<int[]> maxHeap = new PriorityQueue<>((a, b) -> Integer.compare(b[0], a[0]));
// Push points onto the heap, maintaining the size at most k
for (int[] point : points) {
int distance = point[0] * point[0] + point[1] * point[1];
maxHeap.offer(new int[]{distance, point[0], point[1]});
if (maxHeap.size() > k) {
maxHeap.poll(); // Keep the size of the heap at most k
}
}
// Pop elements from the heap and store them in the result
while (!maxHeap.isEmpty()) {
int[] point = maxHeap.poll();
ans.add(Arrays.asList(point[1], point[2]));
}
// Reverse the result to get the closest points first
Collections.reverse(ans);
return ans;
}
public static void main(String[] args) {
// Example usage:
int[][] points = {{2, 3}, {3, 5}, {-2, 2}};
int k = 2;
// Find the k closest points
List<List<Integer>> result = kClosest(points, k);
// Print the result
System.out.println("The " + k + " closest points are:");
for (List<Integer> point : result) {
System.out.println(Arrays.toString(point.toArray()));
}
}
}Output:
The 2 closest points are:
[-2, 2] [2, 3]The time complexity of the algorithm is O(N log K), where N is the number of points and K is the value of k. This complexity arises from the insertion and extraction operations on the priority queue.
The space complexity is O(K) for storing the elements in the priority queue. As we are maintaining our priority queue for k elements only.
You can learn more about min and max heap to better understand it.
Conclusion
We have discussed the leetcode problem of finding the k nearest points to the origin. We learned the max-heap approach to solve it efficiently with codes in C++, Python, and Java. Choosing the appropriate algorithm, and considering time and space complexities are crucial aspects when coding.