Intersection of Two Linked Lists (C++, Java, Python)

In the world of linked lists, there are often situations where two lists intersect. By intersecting, it means that the two lists share a common node from a certain point onwards. This can occur due to programming errors or intentional design choices. In this article, we will try to find the intersection of two linked lists from basic brute force to an optimized approach.

Intersection of Two Linked Lists Problem

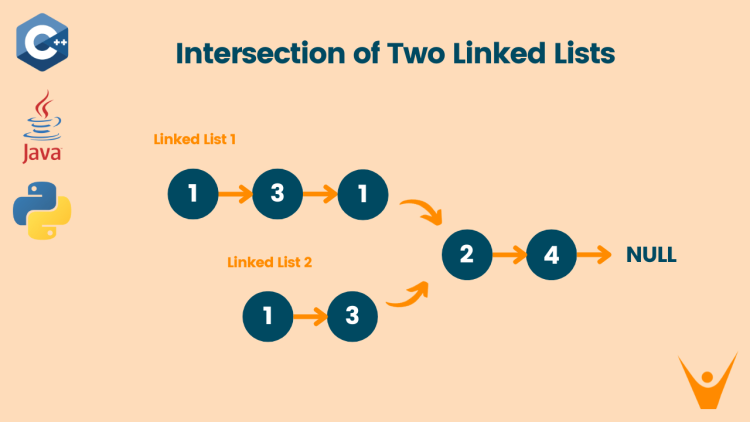
In the Intersection of Two Linked Lists problem, we are given two singly linked lists, let’s call them List 1 and List 2. These lists might have different lengths, and they intersect at some point. Our goal is to develop an algorithm that can efficiently identify the node at which the two lists intersect.

Let’s see an example.

Input: List 1 = [1,3,1,2,4], List 2 = [1,3,2,4]

Output: 2

Example of Intersection of Two Linked Lists

As we can see both the linked lists intersect at node 2.

In the simple brute-force approach, we will iterate through one of the lists and check if each node exists in the other list. If we find a common node, we have found the intersection point. Below are the steps involved:

Firstly we will choose any of the lists and iterate through its nodes.
For each node in List 1, iterate through List 2 and compare each node with the current node from List 1.

If we find a matching node, we have found an intersection point then we will return that node.

If we complete the iteration of List 2 without finding a matching node, there is no intersection between the lists. Return null.

The time complexity is O(m*n) because, for each node in list 2, entire lists 1 are iterated. The space complexity is O(1) as no extra space is required.

Hashing to Find Intersection of Two Linked Lists

The best solution to find the intersection of two linked lists is by using hashing. We will use a hash set to keep track of nodes so that when we find a common node.

Here are the steps used in this approach:

Create a hash table to keep check of the nodes.
Firstly we will Iterate through list 1 and hash its node address.
Then we will iterate through list 2 and search the hashed value in the hash table.
If we find any node address then we will return that node.

The Time Complexity is O(n+m) because iterating through list 1 first takes O(n), then iterating through list 2 takes O(m). The Space Complexity is O(n) because storing list 1 node addresses in unordered_set. Learn more about Hashing in this guide here.

Optimized Approach

In this approach, we will follow the following steps:

We will take two dummy nodes and point each to the head of the lists.

Now we will iterate over them. If anyone becomes null, we will point them to the head of the opposite list and continue iterating until they collide.

Let’s try to understand this approach with an example:

After 2 iterations head 2 will come to NULL.

Now we will point head 2 to the opposite list.

Now we will point head 1 to the opposite list.

Now after 2 iterations, both heads will meet at the intersection point.

C++ Code

Below is the C++ program to find intersection of two linked lists:

#include<bits/stdc++.h>
using namespace std;

class node {
public:
    int num;
    node* next;
    node(int val) {
        num = val;
        next = NULL;
    }
};

// Utility function to insert node at the end of the linked list
void insertNode(node* &head, int val) {
    node* newNode = new node(val);

    if (head == NULL) {
        head = newNode;
        return;
    }

    node* temp = head;
    while (temp->next != NULL) temp = temp->next;

    temp->next = newNode;
    return;
}

// Utility function to check presence of intersection
node* intersectionPresent(node* head1, node* head2) {
    node* d1 = head1;
    node* d2 = head2;

    while (d1 != d2) {
        d1 = (d1 == NULL) ? head2 : d1->next;
        d2 = (d2 == NULL) ? head1 : d2->next;
    }

    return d1;
}

// Utility function to print linked list
void printList(node* head) {
    while (head->next != NULL) {
        cout << head->num << "->";
        head = head->next;
    }
    cout << head->num << endl;
}

int main() {
    // Creation of both lists
    node* head = NULL;
    insertNode(head, 1);
    insertNode(head, 3);
    insertNode(head, 1);
    insertNode(head, 2);
    insertNode(head, 4);
    node* head1 = head;
    head = head->next->next->next;

    // Create the second list
    node* headSec = NULL;
    insertNode(headSec, 1);
    insertNode(headSec, 3);
   
    node* head2 = headSec;
    headSec->next->next = head; // Connect the last node to the intersection point

    // Printing of the lists
    cout << "List1: ";
    printList(head1);
    cout << "List2: ";
    printList(head2);

    // Checking if intersection is present
    node* answerNode = intersectionPresent(head1, head2);
    if (answerNode == NULL)
        cout << "No intersection\n";
    else
        cout << "The intersection point is " << answerNode->num << endl;

    return 0;
}

Java Code

You can do it in Java as well:

import java.util.*;

class Node {
    int num;
    Node next;

    Node(int val) {
        num = val;
        next = null;
    }
}

class Favtutor {
    // Utility function to insert node at the end of the linked list
    static Node insertNode(Node head, int val) {
        Node newNode = new Node(val);

        if (head == null) {
            head = newNode;
            return head;
        }

        Node temp = head;
        while (temp.next != null)
            temp = temp.next;

        temp.next = newNode;
        return head;
    }

    // Utility function to check the presence of intersection
    static Node intersectionPresent(Node head1, Node head2) {
        Node d1 = head1;
        Node d2 = head2;

        while (d1 != d2) {
            d1 = (d1 == null) ? head2 : d1.next;
            d2 = (d2 == null) ? head1 : d2.next;
        }

        return d1;
    }

    // Utility function to print linked list created
    static void printList(Node head) {
        while (head.next != null) {
            System.out.print(head.num + "->");
            head = head.next;
        }
        System.out.println(head.num);
    }

    public static void main(String args[]) {
        // Creation of both lists
        Node head = null;
        head = insertNode(head, 1);
        head = insertNode(head, 3);
        head = insertNode(head, 1);
        head = insertNode(head, 2);
        head = insertNode(head, 4);
        Node head1 = head;
        head = head.next.next.next;

        // Creation of the second list
        Node headSec = null;
        headSec = insertNode(headSec, 1);
        headSec = insertNode(headSec, 3);
        Node head2 = headSec;
        headSec.next.next = head; // Connect the last node to the intersection point

        // Printing of the lists
        System.out.print("List1: ");
        printList(head1);
        System.out.print("List2: ");
        printList(head2);

        // Checking if intersection is present
        Node answerNode = intersectionPresent(head1, head2);
        if (answerNode == null)
            System.out.println("No intersection\n");
        else
            System.out.println("The intersection point is " + answerNode.num);
    }
}

Python Code

Here is the Python solution:

class Node:
    def __init__(self, val):
        self.val = val
        self.next = None

# Utility function to insert a node at the end of the linked list
def insertNode(head, val):
    newNode = Node(val)
    if head is None:
        head = newNode
        return head
    temp = head
    while temp.next is not None:
        temp = temp.next
    temp.next = newNode
    return head

# Utility function to check the presence of an intersection
def intersectionPresent(head1, head2):
    d1 = head1
    d2 = head2
    while d1 != d2:
        # If d1 reaches the end, reset to head2, else move to the next node
        d1 = head2 if d1 is None else d1.next
        # If d2 reaches the end, reset to head1, else move to the next node
        d2 = head1 if d2 is None else d2.next
    return d1

# Utility function to print the linked list
def printList(head):
    while head.next is not None:
        print(head.val, end=' -> ')
        head = head.next
    print(head.val)

if __name__ == '__main__':
    # Creation of the first linked list
    head = None
    head = insertNode(head, 1)
    head = insertNode(head, 3)
    head = insertNode(head, 1)
    head = insertNode(head, 2)
    head = insertNode(head, 4)
    head1 = head
    head = head.next.next.next

    # Creation of the second linked list
    headSec = None
    headSec = insertNode(headSec, 1)
    headSec = insertNode(headSec, 3)
    head2 = headSec
    headSec.next.next = head  # Connect the last node to the intersection point

    # Printing the linked lists
    print('List1: ', end='')
    printList(head1)
    print('List2: ', end='')
    printList(head2)

    # Checking if intersection is present
    answerNode = intersectionPresent(head1, head2)
    if answerNode is None:
        print('No intersection')
    else:
        print('The intersection point is', answerNode.val)

Output:

List1: 1 -> 3 -> 1 -> 2 -> 4
List2: 1 -> 3 -> 2 -> 4
The intersection point is 2

The Time Complexity is O(2*max(length of list1, length of list2)) because the length of the longer list is traversed twice. The Space Complexity is O(1) because no extra space is used.

Finally, here is a comparison of all the three approaches:

Approach	Time complexity	Space complexity	Details
Brute force approach	O(m*n)	O(1)	For each node in list 2, entire lists 1 are iterated.
Hashing Approach	O(n+m)	O(n)	Iterating through list 1 first takes O(n), then iterating through list 2 takes O(m).
Optimized Approach	O(2*max(length of list1,length of list2))	O(1)	length of longer list is traversed twice

Conclusion

In conclusion, we have discussed three approaches to finding the intersection of two linked lists, a commonly asked leetcode problem in technical interviews. We found that traversing through the length of both linked lists optimally helps us to solve this problem more efficiently.