There are many simple technical interview questions with arrays, including finding the missing number. This programming problem incorporates concepts from mathematics, and bit manipulation, and can be solved using hashing and linear search. In this article, we will explore various approaches to solving the Missing Number problem.
What is the Find the Missing Number Problem?
In the Missing Number problem, we have an array of integers containing numbers in a specific range [0 to n], with one number missing from the sequence. Our task is to identify and return the missing number.
Let us understand it better with an example:
Nums = [2,0,1,4,5]
Output = 3
The above array contains all the numbers from 0 to 5 except 3.
Brute Force Approach
Using the simple Brute Force approach, we will try to find every number from 0 to n in the given nums array using linear search and if we are unable to find any number in our array then that number is our missing number.
We will run a nested loop outer loop from 0 to n in our given range:
- For each integer i, we will try to find it in the given array using linear search.
- In the inner loop, we will iterate over the array and consider a bool variable that will tell if the element is present in the array or not firstly we will set the bool to false, and if we will set the bool value to true.
- And if we find a number in the inner array we will break from the inner loop and check for another number.
- After every iteration, we will check our bool if it is false then we will return our number I which is our missing number.
The time complexity of this approach is O(N2), because in the worst case if the missing number is N itself, the outer loop will run N times, and for every number the inner loop will also run for approximately N times. The space complexity O(1) as we are not using any extra space.
Using Hashing to Find the Missing Number
In the Hashing approach to find the missing number, we will use a hash array of size n+1 to store the count of each number. Then we will check the number that is not present.
Let’s say, Nums = [2,0,1,4,5] and N = 5.
Initializing the hash array:
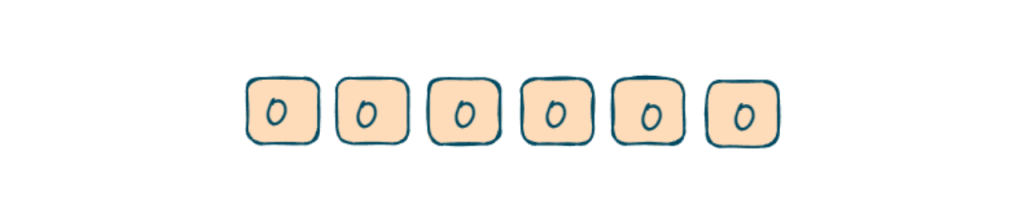
Below are the steps to follow for the hashing approach:
- For every element present in the array we will mark that position as 1 in our hash array because we know that our element is in the range of 0 to N so every index of the hash array represents a number.
- For example, at the 0th index, we have 2 in our nums array. So we will mark the 2nd index as 1.

- Similarly, After marking our hash array for every number present in the nums array our hash array will look like this.

- After marking the hash array for all numbers present in the nums array we will iterate in our hash array and return that index to the hash array where the number is 0.
The time complexity of this approach is O(2*N), O(N) for storing frequencies in the hash array, and O(N) for checking the number with 0 frequency in the hash array.
The space complexity is O(N) where N is the size of array+1. Because we are using an additional hash array. Learn more about hashing in data structures here.
Optimized approach using XOR Operator
We know that the XOR of two numbers is 0 so we can find the missing number using this XOR operator. We will run a loop and calculate the value of XOR of all the elements of the array. Then, if we again XOR this with numbers from 0 to n, the numbers that are already present nullify the effect and what is remaining is our missing number.
Here is how to do it step-by-step:
- In this approach, we will declare two variables with names xor1 and xor2.
- In xor1 we will do bitwise xor of nums array and in xor2 we will do bitwise xor of number from 0 to n using a for loop.
- At last, we will do bitwise xor of xor1 and xor2 and we will get our missing number
- The same number xor gives 0 and one number that is missing will be left at the last
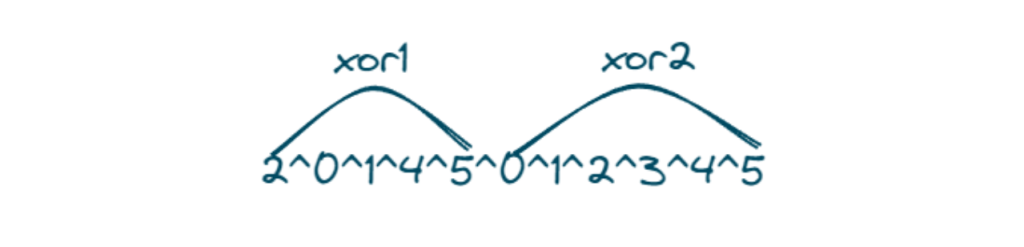
- From this xor1^xor2 we will get our missing number 3.
C++ Code
Here is the C++ program to find the missing number:
#include <iostream>
#include <vector>
using namespace std;
int missingNumber(vector<int>& nums) {
int n = nums.size();
// Initialize XOR results
int xor1 = 0;
int xor2 = 0;
// Calculate XOR of expected values (0 to n) and actual values in the array
for (int i = 0; i <= n; ++i) {
xor1 ^= i;
// XOR each element in the array
if (i < n) {
xor2 ^= nums[i];
}
}
// XOR result will be the missing number
return xor1 ^ xor2;
}
int main() {
// Example usage
vector<int> nums = {2, 0, 1, 4, 5};
int result = missingNumber(nums);
cout << "The missing number is: " << result << endl;
return 0;
}Java Code
Here is the Java program as well:
public class MissingNumber {
public static int missingNumber(int[] nums) {
int n = nums.length;
// Initialize XOR results
int xor1 = 0;
int xor2 = 0;
// Calculate XOR of expected values (0 to n) and actual values in the array
for (int i = 0; i <= n; ++i) {
xor1 ^= i;
// XOR each element in the array
if (i < n) {
xor2 ^= nums[i];
}
}
// XOR result will be the missing number
return xor1 ^ xor2;
}
public static void main(String[] args) {
// Example usage
int[] nums = {2, 0, 1, 4, 5};
int result = missingNumber(nums);
System.out.println("The missing number is: " + result);
}
}Python Code
You can do the same with Python as well:
def missingNumber(nums):
n = len(nums)
# Initialize XOR results
xor1 = 0
xor2 = 0
# Calculate XOR of expected values (0 to n) and actual values in the array
for i in range(n + 1):
xor1 ^= i
# XOR each element in the array
if i < n:
xor2 ^= nums[i]
# XOR result will be the missing number
return xor1 ^ xor2
# Example usage
nums = [2, 0, 1, 4, 5]
result = missingNumber(nums)
print("The missing number is:", result)The time complexity of this approach is O(N) where n is the size of the nums array. Since we are iterating till N two times, we will get linear complexity. The space complexity is O(1) as we are not using any extra space.
Now you have 3 methods, let’s do a small comparative analysis of all of them to find the best one for different situations:
| Approaches | Time complexity | Space complexity | Details |
| Brute force | O(N2) | O(1) | In the worst case if the missing number is N itself, the outer loop will run N times, and for every number the inner loop will also run for approximately N times. |
| Hashing | O(2*N) | O(N) | O(N) for storing frequencies in the hash array, and O(N) for checking the number with 0 frequency in the hash array. |
| Using XOR operator | O(N) | O(1) | O(1) as we are not using any extra space |
Conclusion
In conclusion, the Find the Missing Number leetcode problem can be approached using various methods. We have discussed the approach from brute to hashing to optimal XOR approach.








