Linked lists are the fundamental data structure that provides a dynamic way to store and organize data and one of the problems of linked lists is detecting a cycle in a linked list. In this article, we will discuss the concept of a linked list cycle, and how to detect a cycle or loop in a linked list.
What is the Linked List Cycle Problem?
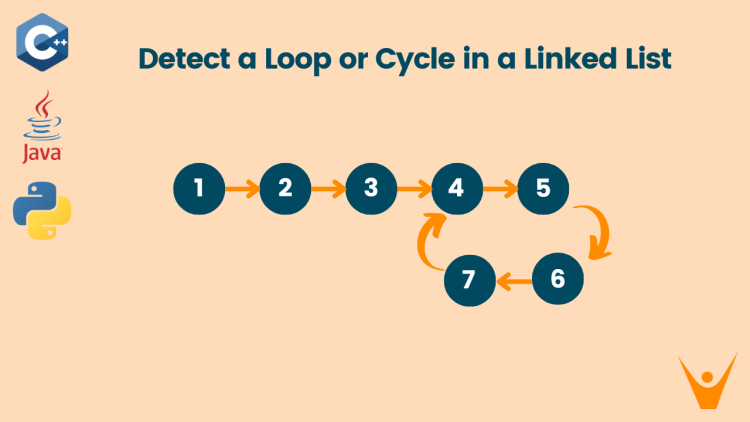
In the Linked List Cycle problem, we are given a linked list and we have to detect a cycle in this linked list, a linked list cycle occurs when a node in the list points to a previous node, creating a loop within the structure.
Let us understand it better with an example:
In the above-linked list, there is a cycle where the last node is connected to the previous node.
Learning about linked list cycles is important for building a strong foundation in computer science. It hones problem-solving skills and provides practical knowledge that can be applied in various real-world scenarios.
Using Hashing to Find Linked List Cycle
In this approach we will use a set data structure because a set data structure only stores unique nodes, if there is any cycle then we will get to know through this set data structure.
Here are the steps to solve the problem using this naive approach:
- Firstly we will declare a set data structure to store unique nodes.
- Now we will start iterating through the list and check if the node is already present in the set or not if it is already present in the set that means there is a cycle
- Let’s implement this approach in the above example.
- Firstly we insert the first node in the set and move our pointer to the node next.
- Now we will insert the 2nd node in our set and move our pointer to the next node.
- Now we will insert the 3rd node in our set and move our pointer to the next node.
- Now we will insert the 4th node in our set and move our pointer to the next node.
- Now we will insert the 5th node in our set and move our pointer to the next node.
- Here we have arrived at the cycle point when we will try to insert this in our set then we will see this node is already present. And return true that there is a cycle.
The time complexity of this approach is O(N) as we are iterating through the list only once and N is the size of the linked list. The space complexity of this approach is O(N) as we are using a set and storing N nodes in it.
Floyd’s Tortoise & Hare Algorithm to Detect Linked List Cycle
Using Floyd’s Tortoise & Hare Algorithm, the concept of the slow and fast pointer is used to detect cycles in a linked list. It is based on the learning that whenever we move a pointer with twice the speed of another pointer if there exists any cycle, both will meet somewhere in the cycle. Since the distance will keep on decreasing between the two after every cycle is completed.
Also known as the cycle detection algorithm Floyd’s Tortoise & Hare Algorithm was developed by Robert W. Floyd. The basic idea behind it is to have two pointers, one moving at a slower pace (tortoise) and the other at a faster pace (hare). If there is a cycle in the sequence, the faster pointer will eventually catch up to the slower one, indicating the presence of a cycle.
Below are the steps to be followed to detect a cycle or loop in a linked list using Floyd’s Tortoise and Hare algorithm:
- Firstly we will Initialise two pointers, slow and fast, at the beginning of the linked list.
- Now Move the slow pointer one step at a time and the fast pointer two steps at a time.
- If there is no cycle, the fast pointer will reach the end of the list (null reference). Else If there is a cycle, the fast pointer will eventually meet the slow pointer within the loop.
- After one more pass, both the pointers met at a point.
C++ Code
Below is the complete C++ program for Linked List Cycle Detection:
#include <bits/stdc++.h>
using namespace std;
// Definition for singly-linked list.
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(nullptr) {}
};
bool hasCycle(ListNode* head) {
// Initialize fast and slow pointers
ListNode* slow = head;
ListNode* fast = head;
// Traverse the linked list
while (fast != nullptr && fast->next != nullptr) {
// Move slow pointer one step
slow = slow->next;
// Move fast pointer two steps
fast = fast->next->next;
// Check if pointers meet, indicating a cycle
if (slow == fast) {
return true;
}
}
// If the end of the list is reached and no cycle is detected
return false;
}
int main() {
// Create a linked list: 1 -> 2 -> 3 -> 4 -> 5 -> 3 (cycle)
ListNode* head = new ListNode(1);
head->next = new ListNode(2);
head->next->next = new ListNode(3);
head->next->next->next = new ListNode(4);
head->next->next->next->next = new ListNode(5);
head->next->next->next->next->next = head->next->next; // Creating a cycle
// Check if the linked list has a cycle
if (hasCycle(head)) {
cout << "The linked list has a cycle." << endl;
} else {
cout << "The linked list does not have a cycle." << endl;
}
return 0;
}Java Code
You can detect loop or cycle in linked list using Java as well:
public class LinkedListCycle {
// Definition for singly-linked list.
static class ListNode {
int val;
ListNode next;
ListNode(int x) {
val = x;
next = null;
}
}
public static boolean hasCycle(ListNode head) {
// Initialize fast and slow pointers
ListNode slow = head;
ListNode fast = head;
// Traverse the linked list
while (fast != null && fast.next != null) {
// Move slow pointer one step
slow = slow.next;
// Move fast pointer two steps
fast = fast.next.next;
// Check if pointers meet, indicating a cycle
if (slow == fast) {
return true;
}
}
// If the end of the list is reached and no cycle is detected
return false;
}
public static void main(String[] args) {
// Create a linked list: 1 -> 2 -> 3 -> 4 -> 5 -> 3 (cycle)
ListNode head = new ListNode(1);
head.next = new ListNode(2);
head.next.next = new ListNode(3);
head.next.next.next = new ListNode(4);
head.next.next.next.next = new ListNode(5);
head.next.next.next.next.next = head.next.next; // Creating a cycle
// Check if the linked list has a cycle
if (hasCycle(head)) {
System.out.println("The linked list has a cycle.");
} else {
System.out.println("The linked list does not have a cycle.");
}
}
}Python Code
Here is the implementation in Python also:
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def hasCycle(head):
# Initialize fast and slow pointers
slow = head
fast = head
# Traverse the linked list
while fast is not None and fast.next is not None:
# Move slow pointer one step
slow = slow.next
# Move fast pointer two steps
fast = fast.next.next
# Check if pointers meet, indicating a cycle
if slow == fast:
return True
# If the end of the list is reached and no cycle is detected
return False
# Create a linked list: 1 -> 2 -> 3 -> 4 -> 5 -> 3 (cycle)
head = ListNode(1)
head.next = ListNode(2)
head.next.next = ListNode(3)
head.next.next.next = ListNode(4)
head.next.next.next.next = ListNode(5)
head.next.next.next.next.next = head.next.next # Creating a cycle
# Check if the linked list has a cycle
if hasCycle(head):
print("The linked list has a cycle.")
else:
print("The linked list does not have a cycle.")Output:
The linked list has a cycle.The time complexity of this approach is O(N) where N is the size of the linked list. In the worst case, all the nodes of the list are visited. The space complexity is O(1) because we are not using any extra space.
Below is a small comparative analysis of both the methods:
| Approaches | Time complexity | Space complexity | Details |
| Hashing Approach | O(N) | O(N) | Here space complexity is O(N) because we are using a set data structure to detect cycle |
| Optimized approach | O(N) | O(1) | Here no extra space is required in this approach |
You might also want to learn how to detect a cycle in an undirected graph as well.
Conclusion
In conclusion, we solve the leetcode problem titled ‘Linked List Cycle’ and how to detect the cycle in a linked list using two different approaches, i.e. using hashing and Floyd’s Tortoise and Hare Algorithm.