Cherry Pickup Problem Solved (C++, Java, Python)

The Dynamic programming method is used in problems where we have to explore all the possibilities and the cherry pickup problem is one of them in which we have to explore all the feasible paths for picking maximum cherries. In this article, we will explore approaches to solve this Cherry Pickup problem from leetcode and how to implement them.

What is the Cherry Pickup Problem?

In the Cherry Pickup problem, we are given a grid that represents a field of cherries, each cell is one of these three possible integers: 0, 1, -1. Among these, an empty cell is represented by 0, a cell that contains cherry is represented by 1, and a cell that thorns is represented by -1.

We have to collect the maximum number of cherries from the fields by following the rules below:

We have to start from (0,0) and reach (n-1,n-1) by moving right and down through valid path cells.
After reaching (n – 1, n – 1) we have to return to (0, 0) by moving left or up through valid path cells.
When we pick a cherry from a valid cell that cell becomes an empty cell.

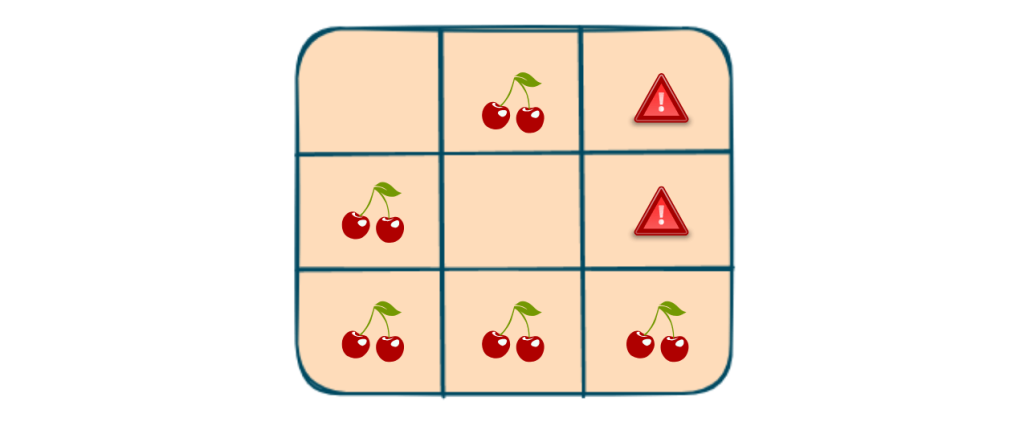
Let’s take an example to solve this problem.

Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]]

Output: 5

Let’s solve it using a dynamic programming approach.

Dynamic Programming Approach

If we want to solve it using dynamic programming, we have to take the cherries in such a way that it takes a maximum of it, reaching (n-1,n-1) from (0,0), if possible and we have to make one traversal from (n-1, n-1) to (0, 0) such that it can take the maximum of the remaining cherries.

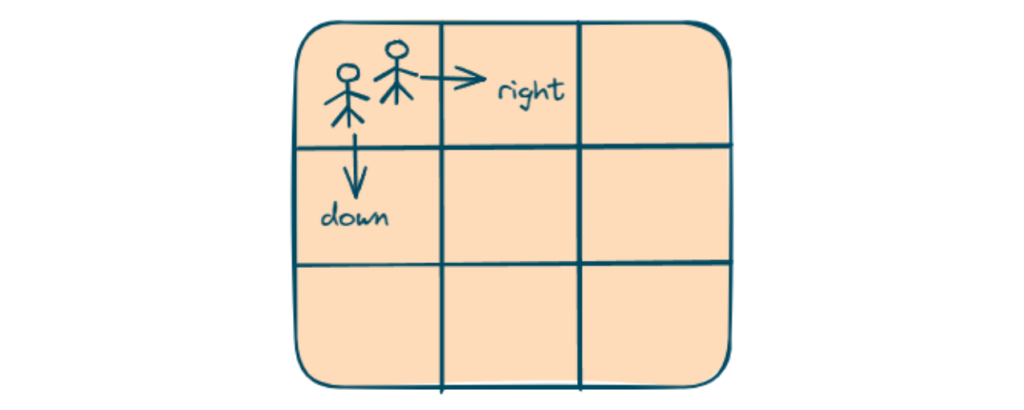
For this, we can think in a way that two people are collecting cherries, and they are following these steps:

In a two-person strategy, we will visualize the two persons simultaneously traversing the grid, each starting from the origin (0, 0) and moving toward the destination (n-1, n-1).
we can say that distance of person1 from origin is equal to distance of person2 from origin i.e r1+c1=r2+c2
At each cell, consider the cherry at the current position of person 1 (grid[r1][c1]).
If person 1 and person 2 are not in the same position (r1 != r2), consider the cherry at the current position of person 2.
They can move in four possible movements (right, right), (right, down), (down, right), and (down, down).

We will Calculate the maximum number of cherries collected at each step by considering all four possibilities.

Some of the edge cases of this problem are:

Either person goes out of bounds or encounters obstacles (-1) in the grid. In such cases, return INT_MIN as it signifies that the path is not possible
If person 1 reaches the destination (n-1, n-1), return the value of the grid at that position.
If both persons reach the destination simultaneously (r1 + c1 = r2 + c2), return the sum of the grid values at that position.
We will use a 3D dynamic programming matrix to store intermediate results, avoiding redundant calculations.
The three dimensions of the matrix represent the positions of the two persons and their distances from the origin.
We will Check if the current state (positions of the two persons) already exists in the 3D dynamic programming matrix. If it does we will return the stored result to optimize computation.

C++ Code

Here is the C++ program to solve the cherry pickup problem using dynamic programming:

#include<bits/stdc++.h>
using namespace std;

int cherryPickupUtil(const vector<vector<int>>& grid, vector<vector<vector<int>>>& dp, int r1, int c1, int r2) {
    int n = grid.size();
    int c2 = r1 + c1 - r2;

    // Check if out of bounds or encountering obstacles
    if (r1 >= n || c1 >= n || r2 >= n || c2 >= n || grid[r1][c1] == -1 || grid[r2][c2] == -1) {
        return INT_MIN;
    }

    // Check if already computed
    if (dp[r1][c1][r2] != -1) {
        return dp[r1][c1][r2];
    }

    // Base case: reached bottom-right corner
    if (r1 == n - 1 && c1 == n - 1) {
        return grid[r1][c1];
    }

    // Calculate cherries collected at the current positions
    int cherries = grid[r1][c1];
    if (r1 != r2) {
        cherries += grid[r2][c2];
    }

    // Calculate the maximum cherries for the two persons' movements
    int maxCherries = cherries + max({
        cherryPickupUtil(grid, dp, r1 + 1, c1, r2 + 1),
        cherryPickupUtil(grid, dp, r1 + 1, c1, r2),
        cherryPickupUtil(grid, dp, r1, c1 + 1, r2 + 1),
        cherryPickupUtil(grid, dp, r1, c1 + 1, r2)
    });

    // Save the result in the memoization table
    dp[r1][c1][r2] = maxCherries;

    return maxCherries;
}

int main() {
    vector<vector<int>> grid = {{0, 1, -1}, {1, 0, -1}, {1, 1, 1}};
    int n = grid.size();

    // Memoization using a 3D vector
    vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(n, -1)));

    // Start the recursion from the top-left corner
    int result = max(0, cherryPickupUtil(grid, dp, 0, 0, 0));

    cout << "Maximum cherries collected: " << result << endl;

    return 0;
}

Java Code

Here is the Java program to solve the cherry pickup problem:

import java.util.Arrays;

public class CherryPickup {

    public static int cherryPickupUtil(int[][] grid, int[][][] dp, int r1, int c1, int r2) {
        int n = grid.length;
        int c2 = r1 + c1 - r2;

        // Check if out of bounds or encountering obstacles
        if (r1 >= n || c1 >= n || r2 >= n || c2 >= n || grid[r1][c1] == -1 || grid[r2][c2] == -1) {
            return Integer.MIN_VALUE;
        }

        // Check if already computed
        if (dp[r1][c1][r2] != -1) {
            return dp[r1][c1][r2];
        }

        // Base case: reached bottom-right corner
        if (r1 == n - 1 && c1 == n - 1) {
            return grid[r1][c1];
        }

        // Calculate cherries collected at the current positions
        int cherries = grid[r1][c1];
        if (r1 != r2) {
            cherries += grid[r2][c2];
        }

        // Calculate the maximum cherries for the two persons' movements
        int maxCherries = cherries + Math.max(
                Math.max(cherryPickupUtil(grid, dp, r1 + 1, c1, r2 + 1),
                        cherryPickupUtil(grid, dp, r1 + 1, c1, r2)),
                Math.max(cherryPickupUtil(grid, dp, r1, c1 + 1, r2 + 1),
                        cherryPickupUtil(grid, dp, r1, c1 + 1, r2)));

        // Save the result in the memoization table
        dp[r1][c1][r2] = maxCherries;

        return maxCherries;
    }

    public static void main(String[] args) {
        int[][] grid = {{0, 1, -1}, {1, 0, -1}, {1, 1, 1}};
        int n = grid.length;

        // Memoization using a 3D array
        int[][][] dp = new int[n][n][n];
        for (int[][] layer : dp) {
            for (int[] row : layer) {
                Arrays.fill(row, -1);
            }
        }

        // Start the recursion from the top-left corner
        int result = Math.max(0, cherryPickupUtil(grid, dp, 0, 0, 0));

        System.out.println("Maximum cherries collected: " + result);
    }
}

Python Code

You can implement it in Python as well:

def cherry_pickup_util(grid, dp, r1, c1, r2):
    n = len(grid)
    c2 = r1 + c1 - r2

    # Check if out of bounds or encountering obstacles
    if r1 >= n or c1 >= n or r2 >= n or c2 >= n or grid[r1][c1] == -1 or grid[r2][c2] == -1:
        return float('-inf')

    # Check if already computed
    if dp[r1][c1][r2] != -1:
        return dp[r1][c1][r2]

    # Base case: reached bottom-right corner
    if r1 == n - 1 and c1 == n - 1:
        return grid[r1][c1]

    # Calculate cherries collected at the current positions
    cherries = grid[r1][c1]
    if r1 != r2:
        cherries += grid[r2][c2]

    # Calculate the maximum cherries for the two persons' movements
    max_cherries = cherries + max(
        cherry_pickup_util(grid, dp, r1 + 1, c1, r2 + 1),
        cherry_pickup_util(grid, dp, r1 + 1, c1, r2),
        cherry_pickup_util(grid, dp, r1, c1 + 1, r2 + 1),
        cherry_pickup_util(grid, dp, r1, c1 + 1, r2)
    )

    # Save the result in the memoization table
    dp[r1][c1][r2] = max_cherries

    return max_cherries


def main():
    grid = [[0, 1, -1], [1, 0, -1], [1, 1, 1]]
    n = len(grid)

    # Memoization using a 3D list
    dp = [[[-1] * n for _ in range(n)] for _ in range(n)]

    # Start the recursion from the top-left corner
    result = max(0, cherry_pickup_util(grid, dp, 0, 0, 0))

    print("Maximum cherries collected:", result)


if __name__ == "__main__":
    main()

Output:

Maximum cherries collected: 5

The time complexity for the dynamic programming approach to solve the cherry pickup problem is O(N³) because it is determined by the number of unique states that the recursive function explores. In this case, the number of unique states is determined by the positions of the two persons and their distances from the origin.

The space complexity for this approach is O(N³) because the 3D array is used for storing the results of subproblems to avoid redundant calculations.

Conclusion

In conclusion, we have used a dynamic programming approach, and the concept of two persons traversing the grid simultaneously, an efficient solution to maximize cherry collection. This strategy ensures that the combined efforts of the two persons result in the optimal collection of cherries.