Binary Search Tree is the most important topic from the interview perspective. It helps you to find the value in the tree in Log(n) time complexity, unlike the normal tree. In this article, we will try the leetcode problem on how to Balance a Binary Search Tree.
Balance a Binary Search Tree problem
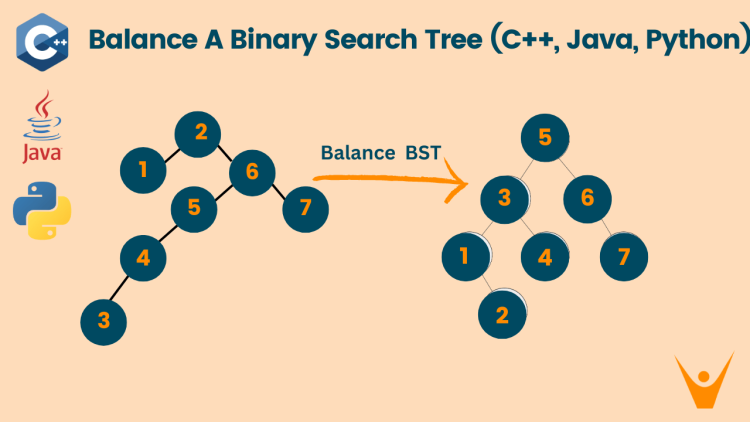
In the Balance BST problem, we have given a binary search tree. We have to create another binary search tree that is a balanced version of the given tree. A balanced BST is a BST in which the absolute difference between the left height – right height <= 1. There may be more than one answer you can return any of them.
Let’s understand this with an example:
Left and right height of the root node.
The Balanced BST of the given tree looks like
An In-order Traversal Approach
In this approach, we will find the in-order traversal of the given BST. After finding the inorder traversal we will create a function that takes the middle element of the inorder traversal and inorder array.
After that, we will call the left side of the middle value to create the left subtree and the right side of the middle value to create the right subtree.
Let’s examine the approach step by step:
- First, create a vector or an array that will store the in-order traversal of the given BST.
- Now create a function name inorder_traversal. Pass the root and the vector into that function.
- Call the same function for the left subtree. Then store the value of the current node in the vector. And call the function for the right subtree.
- Once we get the inorder traversal call the BST function. Pass the vector generated through the in-order function. Pass starting index i.e. 0 and ending index i.e. size of the array.
- Find the middle of the starting and ending index. Call the BST function, passing the left part of the middle value to get the left subtree. Call the BST function, passing the right part of the middle value to get the right subtree.
The below example shows the inorder traversal of the BST.
Let’s examine the code for the above process.
C++ Code
Here is the C++ program to balance a binary search tree:
#include<bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int x){
data = x;
left = NULL;
right = NULL;
}
};
void inorder_traversal(TreeNode* root, vector<TreeNode*>& v){
if(root == NULL) return;
inorder_traversal(root->left, v);
v.push_back(root);
inorder_traversal(root->right, v);
return;
}
TreeNode* BST(int start, int end, vector<TreeNode*>& v) {
if (start > end) return NULL;
int mid = (start + end) / 2;
TreeNode* root = v[mid];
root->left = BST(start, mid - 1, v);
root->right = BST(mid + 1, end, v);
return root;
}
void print_BST(TreeNode* root){
if(root == NULL) return;
print_BST(root->left);
cout<<root->data<<" ";
print_BST(root->right);
return;
}
int main(){
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(4);
root->left->left = new TreeNode(3);
root->left->left->left = new TreeNode(2);
root->left->left->left->left = new TreeNode(1);
vector<TreeNode*>v;
inorder_traversal(root, v);
int n = v.size();
TreeNode* new_root = BST(0, n-1, v);
// in-order traverse of balanced BST
cout<<"inorder traversal of new BST is ";
print_BST(new_root);
return 0;
}Java Code
Here is the Java program to balance a binary search tree:
import java.util.*;
class TreeNode {
int data;
TreeNode left, right;
TreeNode(int x) {
data = x;
left = null;
right = null;
}
}
public class Main {
static void inorderTraversal(TreeNode root, ArrayList<TreeNode> v) {
if (root == null)
return;
inorderTraversal(root.left, v);
v.add(root);
inorderTraversal(root.right, v);
}
static TreeNode BST(int start, int end, ArrayList<TreeNode> v) {
if (start > end)
return null;
int mid = (start + end) / 2;
TreeNode root = v.get(mid);
root.left = BST(start, mid - 1, v);
root.right = BST(mid + 1, end, v);
return root;
}
static void printBST(TreeNode root) {
if (root == null)
return;
printBST(root.left);
System.out.print(root.data + " ");
printBST(root.right);
}
public static void main(String[] args) {
TreeNode root = new TreeNode(5);
root.left = new TreeNode(4);
root.left.left = new TreeNode(3);
root.left.left.left = new TreeNode(2);
root.left.left.left.left = new TreeNode(1);
ArrayList<TreeNode> v = new ArrayList<>();
inorderTraversal(root, v);
int n = v.size();
TreeNode newRoot = BST(0, n - 1, v);
// Inorder traversal of balanced BST
System.out.print("Inorder traversal of new BST is ");
printBST(newRoot);
}
}
Python Code
We can implement it in Python also:
class TreeNode:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
def inorder_traversal(root, v):
if root is None:
return
inorder_traversal(root.left, v)
v.append(root)
inorder_traversal(root.right, v)
def BST(start, end, v):
if start > end:
return None
mid = (start + end) // 2
root = v[mid]
root.left = BST(start, mid - 1, v)
root.right = BST(mid + 1, end, v)
return root
def print_BST(root):
if root is None:
return
print_BST(root.left)
print(root.data, end=" ")
print_BST(root.right)
if __name__ == "__main__":
root = TreeNode(5)
root.left = TreeNode(4)
root.left.left = TreeNode(3)
root.left.left.left = TreeNode(2)
root.left.left.left.left = TreeNode(1)
v = []
inorder_traversal(root, v)
n = len(v)
new_root = BST(0, n - 1, v)
# In inorder to traverse of balanced BST
print("inorder traversal of new BST is ", end="")
print_BST(new_root)Output:
inorder traversal of new BST is 1 2 3 4 5 The time complexity to balance a binary search tree using in-order traversal is O(n), Where n is the total number of nodes present in the given BST. As we are calling two functions one is inorder_traversal and another is BST both time complexity is O(n).
The space complexity is also O(n). We are storing the values of nodes in the array.
Conclusion
In this article, we solved the Blaance Binary Search Tree problem from leetcode. Remember that if BST is not balanced then the searching operation may take O(n) time. But by balancing the BST time and complexity will reduced to O(log(n)).