There are many leetcode problems associated with arrays that are being asked in interviews, one of them is finding the minimum in the rotated sorted array. This article will delve into the various approaches to finding the minimum element in a rotated sorted array, with code implementation.
Find Minimum in the Rotated Sorted Array Problem
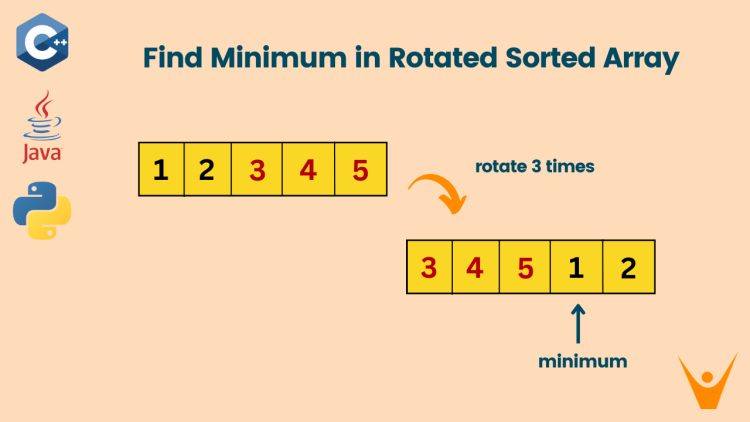
In the programming problem to find the minimum in the rotated sorted array, we are given a sorted array that has been rotated between 1 and n times. Our task is to find the minimum element in this rotated sorted array. It is important to note that all elements in the array are unique.
Rotating an array [a[0], a[1], a[2], …, a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], …, a[n-2]].
Let us understand it with an example:
Input: nums = [3,4,5,1,2]
Output: 1
Note that the original array was [1,2,3,4,5] rotated 3 times.
Let’s discuss the easy solution using linear search. In this approach of finding the minimum element, we will traverse the whole array from start to end comparing each element to find the minimum. Here are the steps involved:
- First of all, we will declare a variable to store the minimum element and initialize it with the first element of the array
- Now we will start traversing from 2nd element to the last and compare each element with the minimum element. If a smaller element is found, we will update the minimum element
- After traversing the entire array, the minimum element will be stored in the variable
- Now we will return the minimum element.
The Time Complexity of this approach is O(N), where n is the size of the array. The Space Complexity is O(1) as we haven’t used any extra space.
Using Binary Search to Solve It
The best possible way to find the minimum in a rotated sorted array is by using Binary Search. We know that we can apply binary search in a sorted array and a rotated sorted array. We have two sorted halves and we have to detect in which half minimum element is present.
Binary Search and Linear Search are the two most used searching algorithms in any programming language.
Let’s do it step-by-step:
- Firstly we will initialize two variables ‘low’ and ‘high’ to the first and last indices of the array and mid is calculated as the middle index using the formula ‘low + (high-low)/2’.
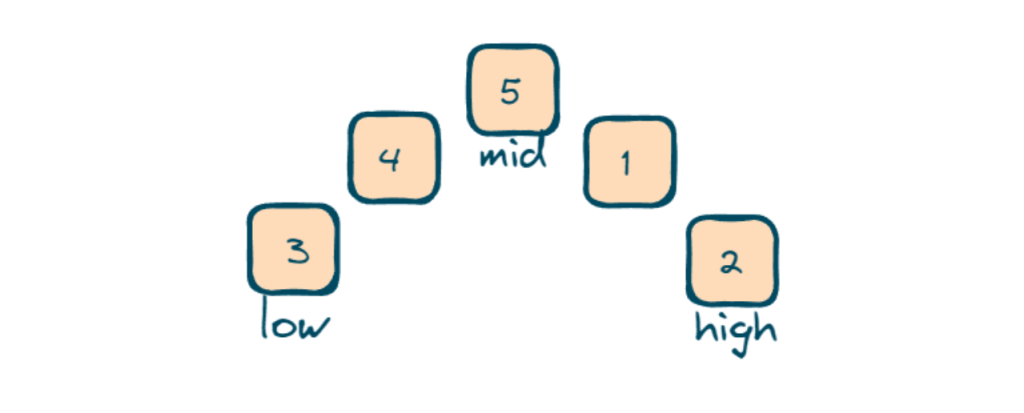
- ‘ans’ is initialized to INT_MAX to keep track of the minimum element.
- Now we will run a while loop as long as ‘low’ is less than or equal to ‘high’.
- Inside the loop, we will check whether the segment of the array from ‘low’ to ‘mid’ is sorted, by checking nums[low]<=nums[mid] (3<=5).
- If true we will update ‘ans’ with the minimum of current ‘ans’ and ‘nums[low]’ and adjust the search range by updating ‘low’ to ‘mid+1’.
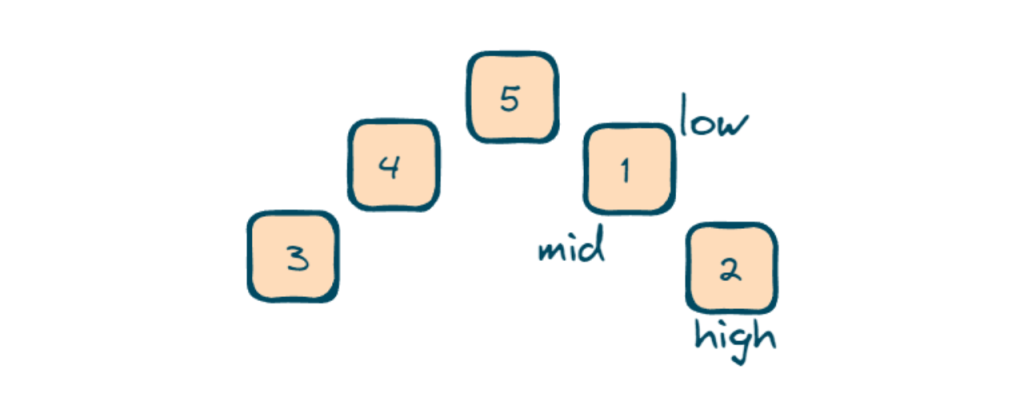
- If the segment is not sorted, it means the rotation point is in the current segment. It updates ans with the minimum of the current ans and nums[mid] and adjusts the search range by updating ‘high’ to ‘mid-1’.
- The mid is then recalculated using the formula low + (high – low) / 2.
- The loop continues until the low is greater than the high, at which point the search range has converged
C++ Code
Let’s implement it in C++:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int findMin(vector<int>& nums) {
int n = nums.size();
int low = 0;
int high = n - 1;
int mid = low + (high - low) / 2;
int ans = INT_MAX;
while (low <= high) {
if (nums[low] <= nums[mid]) {
ans = min(ans, nums[low]);
low = mid + 1;
} else {
ans = min(ans, nums[mid]);
high = mid - 1;
}
mid = low + (high - low) / 2;
}
return ans;
}
int main() {
vector<int> rotatedArray = {3,4,5,1,2};
int minElement = findMin(rotatedArray);
cout << "Minimum Element: " << minElement << endl;
return 0;
}Python Code
We can do the binary search approach in Python as well:
def find_min(nums):
n = len(nums)
low = 0
high = n - 1
ans = float('inf')
while low <= high:
mid = low + (high - low) // 2
if nums[low] <= nums[mid]:
ans = min(ans, nums[low])
low = mid + 1
else:
ans = min(ans, nums[mid])
high = mid - 1
return ans
rotated_array = [3, 4, 5, 1, 2]
min_element = find_min(rotated_array)
print("Minimum Element:", min_element)Java Code
Finally, here is the Java program to find minimum in rotated sorted array:
import java.util.Arrays;
public class FindMin {
public static int findMin(int[] nums) {
int n = nums.length;
int low = 0;
int high = n - 1;
int ans = Integer.MAX_VALUE;
while (low <= high) {
int mid = low + (high - low) / 2;
if (nums[low] <= nums[mid]) {
ans = Math.min(ans, nums[low]);
low = mid + 1;
} else {
ans = Math.min(ans, nums[mid]);
high = mid - 1;
}
}
return ans;
}
public static void main(String[] args) {
int[] rotatedArray = {3, 4, 5, 1, 2};
int minElement = findMin(rotatedArray);
System.out.println("Minimum Element: " + minElement);
}
}Output:
Minimum Element: 1The time complexity is O(log N), where N is the size of the input array nums. The binary search algorithm is used to find the minimum element, and in each iteration, the search range is effectively halved. The Space complexity is O(1) as we haven’t used any extra space.
Before ending this tutorial, let’s compare both the approaches:
| Approach | Time complexity | Space complexity | Details |
| Linear search Approach | O(N) | O(1) | As we are traversing through the array only once to check the minimum element. |
| Binary search Approach | O(Nlogn) | O(1) | The binary search algorithm is used to find the minimum element, and in each iteration, the search range is effectively halved. |
Conclusion
In conclusion, the leetcode problem of finding the minimum element in a rotated sorted array has been addressed through both a brute-force linear search and an optimized binary search approach, with their time complexity and space complexity and implementation in C++, Java, and Python.